CF506E Mr. Kitayuta's Gift 的题解

CF506E Mr. Kitayuta's Gift

先假设 \(n+\left|s\right|\) 为偶数。

考虑一个 \(dp\)，设 \(f_{i,l,r}\) 表示考虑了最终回文串的前后 \(i\) 个字符，\(s\) 尽可能匹配后还剩下 \([l,r]\) 的情况，这样子可以防止算重。

那么，你把它的转移画出来，大概是这样子的（自环数量其实就是 dp 转移过程中 \(f_{i,l,r}\to f_{i+1,l,r}\) 乘上的系数）：

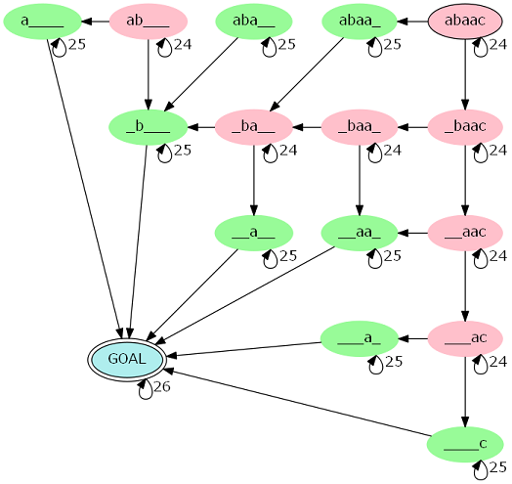
其中 GOAL 代表匹配完毕；红点代表的状态两端的字符不相同；绿点代表的状态两端的字符相同。注意，能转移到 GOAL 的点都是绿点。

这个自动机建立出来节点数量为 \(\left|s\right|^2\)，难以在上面进行 dp 的优化，但事实上，整个自动机可以被拆分为若干条链，且一条链上若有 \(x\) 个红点，那么就有 \(\lceil\frac{\left|s\right|-x}{2}\rceil\) 个绿色的点。（对应下图上半部分）

并且，有意思的是，当我们把他拆为若干条链的时候，实际上我们并不关心红色点和绿色点的顺序了，因为实际上自环表示乘法，到下一个节点表示赋值，那么顺序其实不影响。

也就是说，我们只有 \(\mathcal{O}(\left|s\right|)\) 条本质不同的链，那么设 \(dp_{i,l,r}\) 从起点走到 \((l,r)\) 对应的节点的路径中，经过 \(i\) 个红点的路径数量，那么记忆化 \(dp\) 做到 \(\mathcal{O}(\left|s\right|^3)\)，就可以求出每条本质不同的链的数量。

这样，我们可以对每条链做矩阵乘法，时间为 \(\mathcal{O}(\left|s\right|^4\log n)\)。

还是不优啊，但是我们可以参考网络流的建模方式，合并一下相同部分（对应下图下半部分），那么只有 \(\mathcal{O}(\left|s\right|+\frac{\left|s\right|}{2})\) 个点。

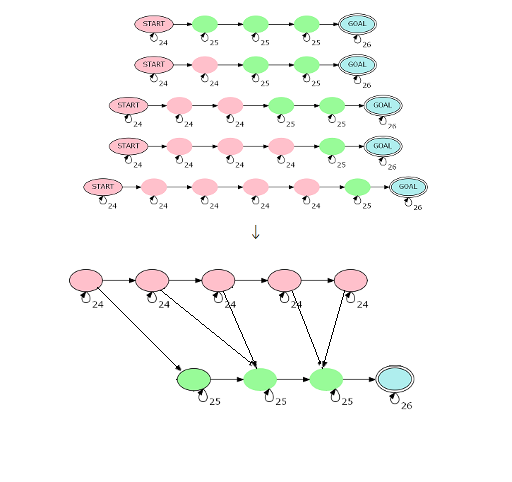
然后你就可以利用矩阵乘法优化 dp 了。

具体来说，有 \(\left|s\right|-1\) 个红点，\(\lceil\frac{\left|s\right|}{2}\rceil\) 个绿点，\(1\) 个蓝点。

红点到下一个红点为 \(1\)，绿点到下一个绿点为 \(1\)，经过 \(x\) 个红点到绿点（代表有多少个 \(x\) 个红点的链），以及自环，设这个矩阵为 \(B\)。（其实类似邻接矩阵连边）

那么答案为 \(A\times B^{n+\left|s\right|}\)，\(A\) 的第一个为 \(1\)，第 \(\left|s\right|\) 个为有多少个没有红点的链。

如何处理 \(n+\left|s\right|\) 为奇数的情况？

当我们转移到最终节点的时候，形如 \([i,i+1]\) 的绿点是无法转移的，那么我们只考虑 \([i,i+1]\) 作为最后一个状态的情况，然后再跑一遍即可，记得把蓝点置为无自环。

需要注意的是，\(B\) 是一个三角矩阵（\((i,k)\gets(i,j)\times (j,k),i\le j\le k\)），且 \(A\) 只有第一行，由此优化复杂度。

#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define p_b push_back
#define m_p make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define gcd __gcd
#define lowbit(x) (x&(-x))
using namespace std;

const int N=205,M=305,INF=0x3f3f3f3f,mod=10007;
void add(int &x,int y){
    x+=y;
    if(x>=mod) x-=mod;
}
int n,m,l;
char s[N];
struct matrix{
    int a[M][M]={0};
    friend void operator*(matrix &x,const matrix &y){
        matrix z;
        for(int i=1;i<=l;i++)for(int j=i;j<=l;j++)for(int k=j;k<=l;k++) add(z.a[i][k],x.a[i][j]*y.a[j][k]%mod);
        x=z;
    } 
    friend void operator^(matrix &x,const matrix &y){
        matrix z;
        for(int i=1;i<=l;i++)for(int j=1;j<=l;j++)add(z.a[1][i],x.a[1][j]*y.a[j][i]%mod);
        x=z;
    }
}A,B,_A,_B;

void ksm(int k){
    while(k){
        if(k&1) A*B;
        B*B;k>>=1;
    }
}
int vis[N][N][N],f[N][N][N];
int dp(int i,int l,int r){
    if(i<0||l<=0||r>m||l>r)return 0;
    if(vis[i][l][r]) return f[i][l][r];
    vis[i][l][r]=1;
    if(l==1&&r==m) return f[i][l][r]=(i==0);
    if(l!=1&&s[l-1]!=s[r]) add(f[i][l][r],dp(i-1,l-1,r));
	if(r!=m&&s[l]!=s[r+1]) add(f[i][l][r],dp(i-1,l,r+1));
    if(l!=1&&s[l-1]==s[r+1]) add(f[i][l][r],dp(i,l-1,r+1));
    return f[i][l][r];
}
int main(){
    scanf("%s%d",s+1,&n);m=strlen(s+1);l=m+(m+1)/2;
    for(int i=0;i<m;i++){
        int tmp=0;
        for(int j=1;j<=m;j++){
            add(tmp,dp(i,j,j));
            if(j!=m&&s[j]==s[j+1])add(tmp,dp(i,j,j+1));
        }
        if(i){
            B.a[i][i]=24,B.a[i][l-(m-i+1)/2]=tmp;
            if(i==1) A.a[1][1]=1;
            else B.a[i-1][i]=1;
        }
        else{
            A.a[1][m]=tmp,B.a[l][l]=26;
            for(int j=m;j<l;j++) B.a[j][j]=25,B.a[j][j+1]=1;
        }
    }
    _A=A,_B=B;ksm((n+m+1)/2);
    int ans=A.a[1][l];
    if(!((n+m)&1)){printf("%d\n",ans);return 0;}
    A=_A,B=_B;
    for(int i=0;i<m;i++){
        int tmp=0;
        for(int j=1;j<=m;j++) if(j!=m&&s[j]==s[j+1])add(tmp,dp(i,j,j+1));
        if(i) B.a[i][l-(m-i+1)/2]=tmp;
        else A.a[1][m]=tmp,B.a[l][l]=0;
    } 
    ksm((n+m+1)/2);
    add(ans,mod-A.a[1][l]);printf("%d\n",ans);
    return 0;
}