TJ - [CF1313D] Happy New Year

[CF1313D] Happy New Year

难度：2500

\(2s,500MB\)

一，题目：

题目大意：

给你一个长度为\(m\)的序列\(a\)，初始值为\(0\)，现在有\(n\)个操作，第\(i\)操个操作是将区间\([L_i,R_i]\)内的元素的值都加\(1\)，你可以选择进行任意个操作，但每个操作都只能进行一次。问你最多可以使得多少个元素的值为奇数。

题目会保证若将所有操作都进行后，每个元素最大为\(k\)。

数据范围：

\(1\le n \le 1\times 10^5,1\le m \le 1\times 10^9,1\le k \le 8\)。

读入格式：

第一行\(n,m,k\)。

接下来的\(n\)行，第\(i+1\)行为\(L_i,R_i\)。

样例输入：

3 5 3
1 3
2 4
3 5

样例输出：

4

二，solution：

先把题意转化一下：

我们可以把\(a\)抽象为一个长度为\(m\)的数轴，每个操作其实就是用一个线段覆盖\([L_i,R_i]\)这个区间，问你最多有几个点被覆盖被覆盖了奇数次，如下图（样例）：

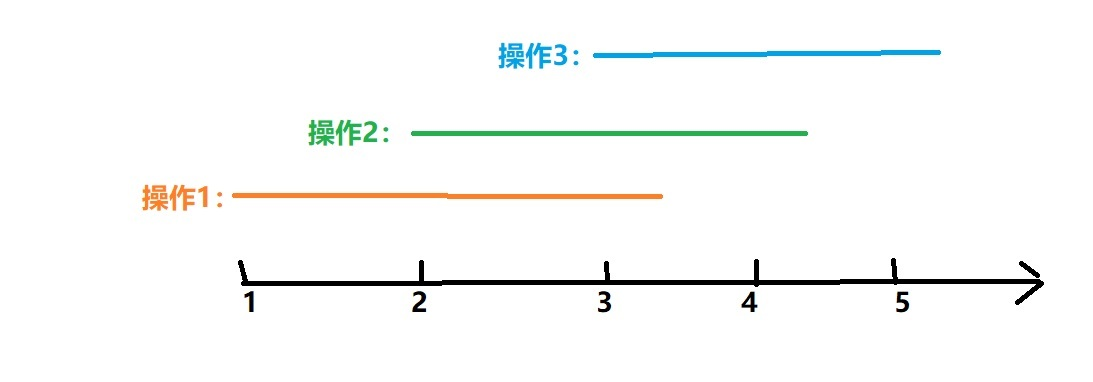
看到这个\(k\le 8\)，（代表一个点最多被\(k\)条线覆盖），自然而然的想到状压\(DP\)。

不妨设\(f[i][S]\)表示第\(i\)个点被集合为\(S\)的这些线覆盖住。

但是，这个集合\(S\)中每一位所代表的点是一直在变化的，怎么办呢？

我们设\(vis[i]\)表示当前\(S\)的第\(i\)位代表的线段的编号，在每次有线段加入\退出的时候，利用\(vis\)进行更改即可。

加入：

for(int j=0;j<k;j++){
    if(vis[j]==0){
        now=j;//now表示当前处理到的线段对应的二进制位
        vis[j]=id;//标记一下,id
        break;
    }
}

退出：

for(int j=0;j<k;j++){
    if(-id==vis[j]){
        vis[j]=0;//清空
        now=j;//now表示当前处理到的线段对应的二进制位
        break;
    }
}

但是\(m\)最大有\(10^9\)，时间复杂度为\(\mathcal{O}(M\times 2^k)\)，绝对会\(TLE\)，若不进行滚动数组优化的话空间也受不了。

需要优化

我们发现，操作的个数是\(1\times 10^5\)，若把上面的那个\(M\)换为\(N\)，就可以接受了。

不妨把每个操作抽象为两个二元组扫描线\((L_i,i)\)和\((R_i+1,-i)\)。（第二位为整数表示是一个操作的开头，否则为结尾），分别表示从这个点开始就多了/少了一条线段。

这样子，最多会有\(2\times n\)个点，空间复杂度可以接受。

我们在把这些扫描线排序后，很明显，在相邻的两条扫描线中间的元素被覆盖的情况是可以用同一个二进制数表示的。

设\(f[i][S]\)表示第\(i\)个扫描线，此时使用了集合为\(S\)的这些线段。（则代表当前这个扫描线到下一条扫描线之间的左闭右开的区间被覆盖情况都为\(S\)）。

好了，接下来正儿八经的推式子：

设\(len\)表示当前这个扫描线到下一条扫描线的长度，\(now\)表示当前的扫描线在\(S\)中对应的二进制位，\(ask(S)\)表示\(S\)二进制下是否有奇数个一。

若这个扫描线为线段的左端点，则：

\[f[i][j]= \begin{cases} f[i-1][j]+len\cdot ask(j)& \text{j二进制下第now位为0}\\ f[i-1][j\oplus(1<<now)]+len\cdot ask(j)&\text{j二进制下第now位为1} \end{cases} \]

若这个扫描线为线段的右端点，则：

\[f[i][j]= \begin{cases} \max\{f[i-1][j],f[i-1][j\oplus(1<<now)]\}+len\cdot ask(j)&\text{j二进制下第now位为0} \\INF&\text{j二进制下第now位为1} \end{cases} \]

初始化时，其他\(f[i][j]\)都为\(-INF\)，\(f[0][0]=0\)。

\(f[n*2][0]\)即为所求，因为最后一个扫描线一定是代表右端点，则他一定不会被任何一条线覆盖。

好了，最后注意一下，将扫描线进行排序时，同一个点上，代表右端点的扫描线因该在左端点的扫描线前。

另外，这道题其实可以用将第\(i\)维优化掉或者用滚动数组，感兴趣的可以写一写。

代码：

#include<bits/stdc++.h>
#define ll long long
#define m_p make_pair
using namespace std;
const int N=1e5+5,K=8;
int n,m,k;
int f[N*2][(1<<K)];//到第i条线时，用了的线的集合为j，最多高兴的孩子的数量 
vector<pair<int,int> > a;
int vis[K];

inline int ask(int x){//x二进制下是否有奇数个一。
	int sum=0;
	while(x){
		if(x&1) sum++;
		x>>=1;
	}
	return (sum&1);
}

int main(){
	scanf("%d%d%d",&n,&m,&k);
	int l,r;
	for(int i=1;i<=n;i++){
		scanf("%d%d",&l,&r);
		a.push_back(m_p(l,i));
		a.push_back(m_p(r+1,-i));//处理为两条扫描线
	}
	sort(a.begin(),a.end());//进行排序
    //初始化：
	memset(f,0xcf,sizeof(f));
	f[0][0]=0;
	for(int i=1;i<=n*2;i++){
		int id=a[i-1].second;
		int len= (a[i-1].first==a[n*2-1].first) ? 0 : a[i].first-a[i-1].first;//注意，最后一个点的扫描线代表的区间长度为0
		int now;//当前的扫描线在对应的二进制位
		if(id<0){//右端点 
			for(int j=0;j<k;j++){
				if(-id==vis[j]){
					vis[j]=0;
					now=j;
					break;
				}
			}
			for(int j=0;j<(1<<k);j++){
				if((j>>now)&1) f[i][j]=0xcfcfcfcf;
				else f[i][j]=max(f[i-1][j],f[i-1][j^(1<<now)])+len*ask(j);
			}
		}
		else{//左端点 
			for(int j=0;j<k;j++){
				if(vis[j]==0){
					now=j;
					vis[j]=id;
					break;
				}
			}
			for(int j=0;j<(1<<k);j++){
				if((j>>now)&1) f[i][j]=f[i-1][j^(1<<now)]+len*ask(j);
				else f[i][j]=f[i-1][j]+len*ask(j);
			}
		}
	}
	cout<<f[n*2][0];//最后一个扫描线一定是代表右端点，则他一定不会被任何一条线覆盖。
	return 0;
}