算法设计与实践作业12

1.     问题

给定无向连通图G和m种颜色，用这些颜色给图的顶点着色，每个顶点一种颜色。如果要求G的每条边的两个顶点着不同颜色。给出所有可能的着色方案；如果不存在，则回答“NO”。

 

2.     解析

设G有n个顶点，将顶点编号为1,2，……,n,则搜索空间为深度n的m叉完全树，将颜色编号为1,2,…,m结点<x₁,x₂,…x₃,x_k>(x₁,x₂,…,x_k∈{1,…,m},1<=k<=n)表示顶点1的颜色x₁，顶点2的颜色x₂,…,顶点k的颜色x_k。

 

 

 

 

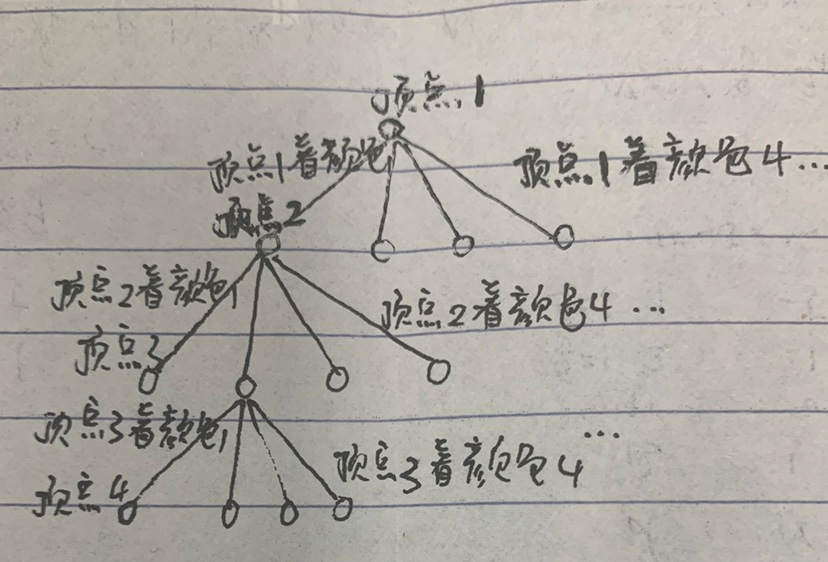
3.     设计

 

输入：无向图G=（V,E）。

输出：G的顶点3着色c[1…n],其中每个c[j]为1,2或3。

For k←1 to n

   C[k]←0

End for

Flag←false

Graphcolor(1)

If flag then output c

Else output “no solution”

过程graphcolor(k)

For color=1 to 3

C[k]←color

If c为合法着色 then set flag←true and exit

Else if c是部分的 then graphcolor(k+1)

End for

4.     分析

结果运行：

 

 

 

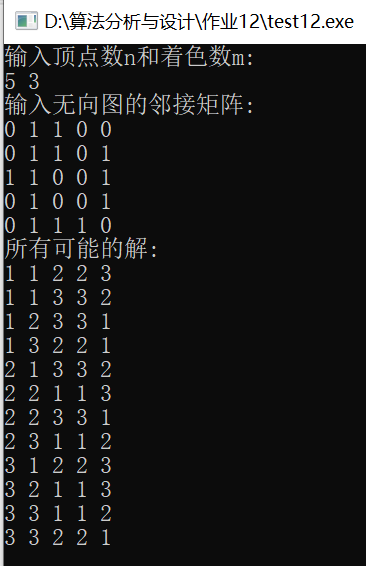
搜索树有：1+m+m^2+…+m^n=(m^(n+1)-1)/(m-1)<=(m^(n+1))/(m/2)=2*m^n,m>=2个结点。每个节点要与其他所有顶点的颜色进行n-1次比较，时间复杂度为O(nm^n)

5.     源码

github地址：https://github.com/122cmy/myGitTemp12

博客地址：https://www.cnblogs.com/122cmy/