算法分析与设计实践作业1

1.     问题

举一个实例，画出采用Prim算法构造最小生成树的过程

举一个实例，画出采用Kruskal算法构造最小生成树的过程

2.     解析

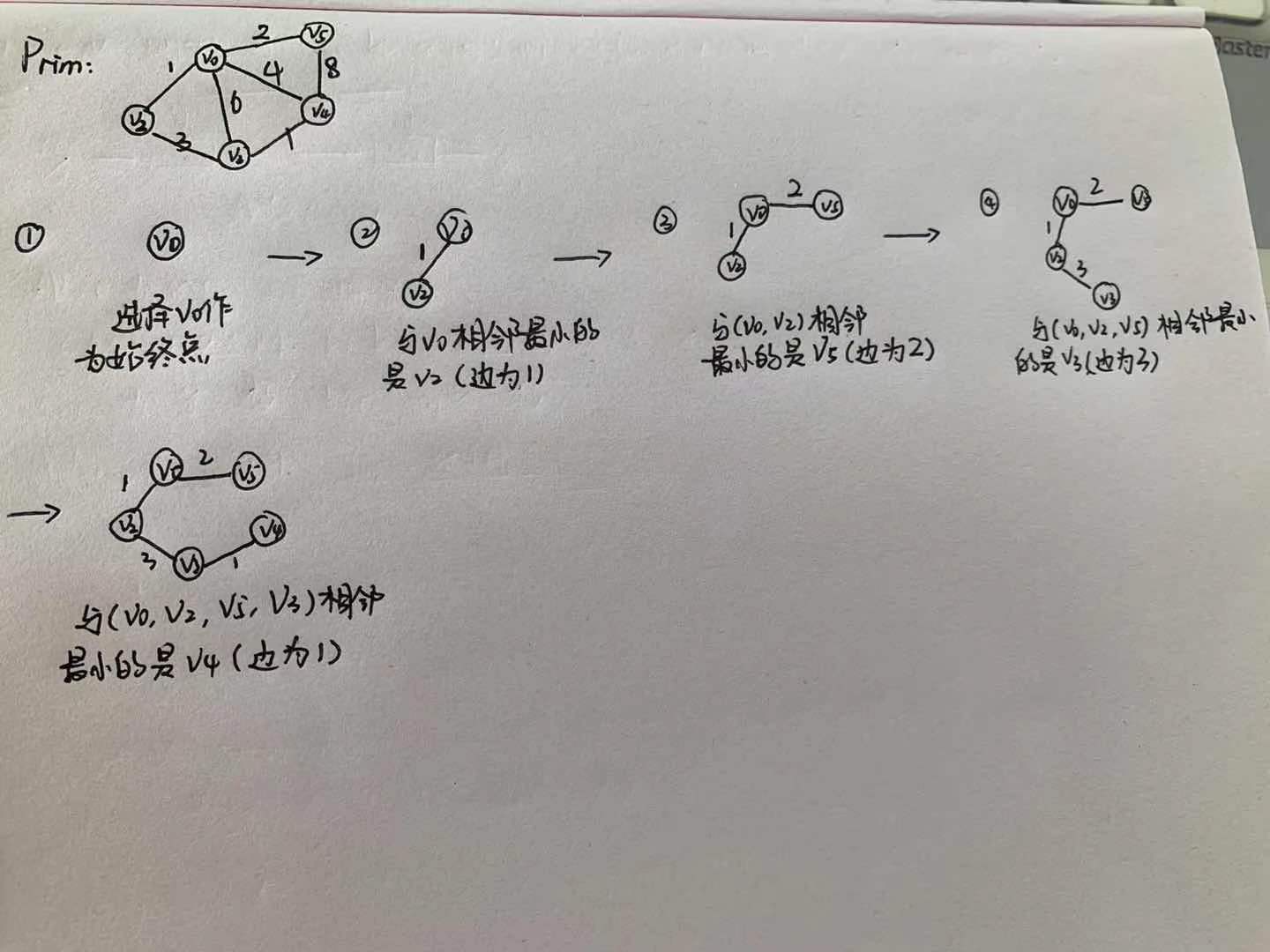
Prim：连通无向图G=（V,E）,V’是最小生成树的顶点集，E’是最小生成树的边集。开始时，任选一顶点加入V’,然后找出V’和剩下未被收录的相邻顶点权值最小的边，将顶点加入V’,将边加入E’,直到V=V’,边的数量=顶点数-1，最后得到最小生成树T=（V’,E’）。示例如下：

 

 

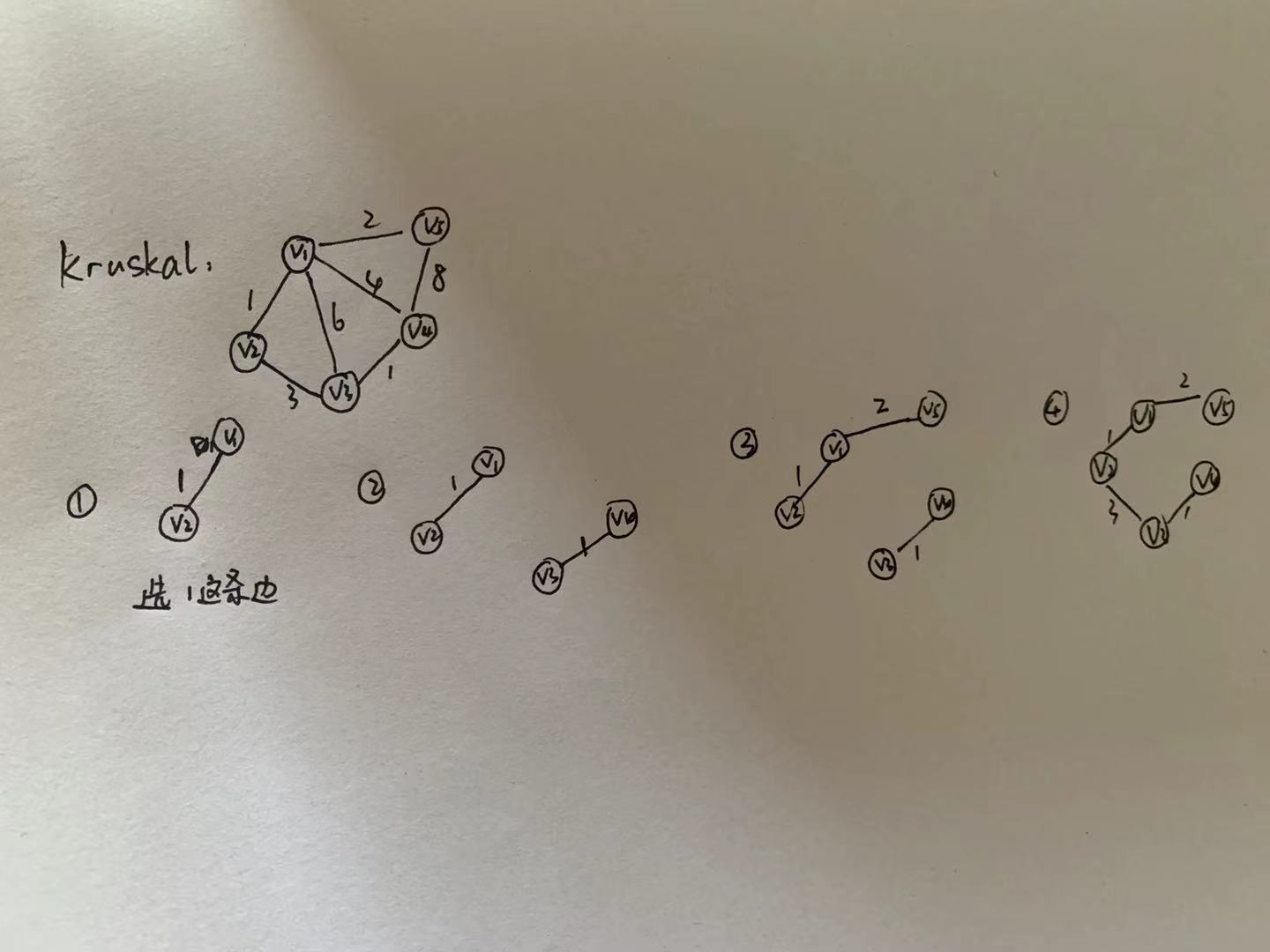
Kruskal：这里把每一个节点看成一棵树，将所有边按权值大小进行排序，选择最小权值且不会与之前的边构成回路的边（即两个节点是否在同一集合上，如果不在同一集合上，则并合），直到V=V’,边的数量=顶点数-1，最后得到最小生成树T=（V’,E’）。示例如下：

 

3.     设计

[核心伪代码]

Prim算法：

T={}

任取一初始点

找相邻点最小的边

If（（v,w）不产生环）

  add(v,w)  to T

else

  discard （v,w）

if（T少于n-1条边）

  printf（“不能构成最小生成树”）

 

 

Kruskal算法：

T={}

从所有边中找到最小边

If（（v,w）不产生环）

  add(v,w)  to T

else

  discard （v,w）

if（T少于n-1条边）

  printf（“不能构成最小生成树”）

 

 

4.     分析

结果如图：

Prim算法：O（n*n），适用于顶点少边稠密的网络

 

 

 

 

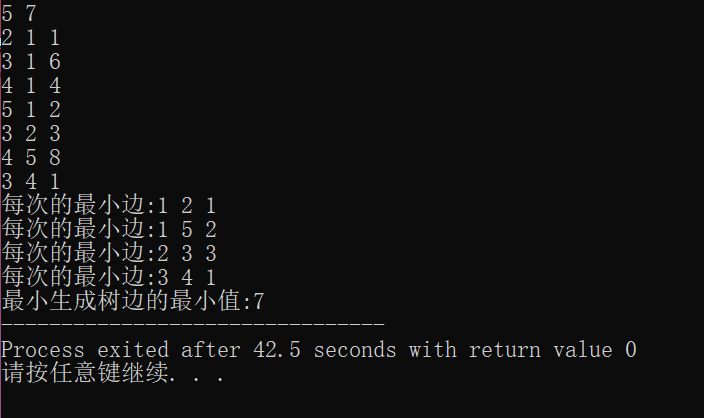
Kruskal：O（eloge），适用于顶点多边少的稀疏的图

 

 

 

5.     源码

https://github.com/122cmy/myGitTemp1