多变量高斯分布采样

已知均值\(\bm{\mu}^*\) 和协方差矩阵\(\bm{\Sigma}^*\), 得到样本 \(\bm{\theta} \sim N(\bm{\mu}^*, \bm{\Sigma}^*)\)

Matlab 实现代码：

% Example of sampling from multivariate Gaussian distribution via Cholesky
% decomposition
Sigma = [2, -1; -1, 2]; % 协方差矩阵，必须为正定矩阵
mu = [2, 5]; % 均值
dim = size(Sigma, 1); % 样本维度
n = 10000; % 样本数量
L_chol = chol(Sigma, 'lower'); % get the loweer triangle matrix, L_chol*Lchol' = Sigma
tmp = randn(n, dim); % tmp ~ N(0, I)
mu_vec = repmat(mu, n, 1); % 均值向量, size(mu_vec) = (n, dim)
samples = (L_chol*tmp')'; % samples ~ C*N(0,I), size(samples) = (n, dim)
theta = mu_vec + samples;
[h,ax,B,P]= plotmatrix(theta)
ax(1,1).YLabel.String='\theta_1'; 
ax(2,1).YLabel.String='\theta_2'; 
ax(2,1).XLabel.String='\theta_1';
ax(2,2).XLabel.String='\theta_2';

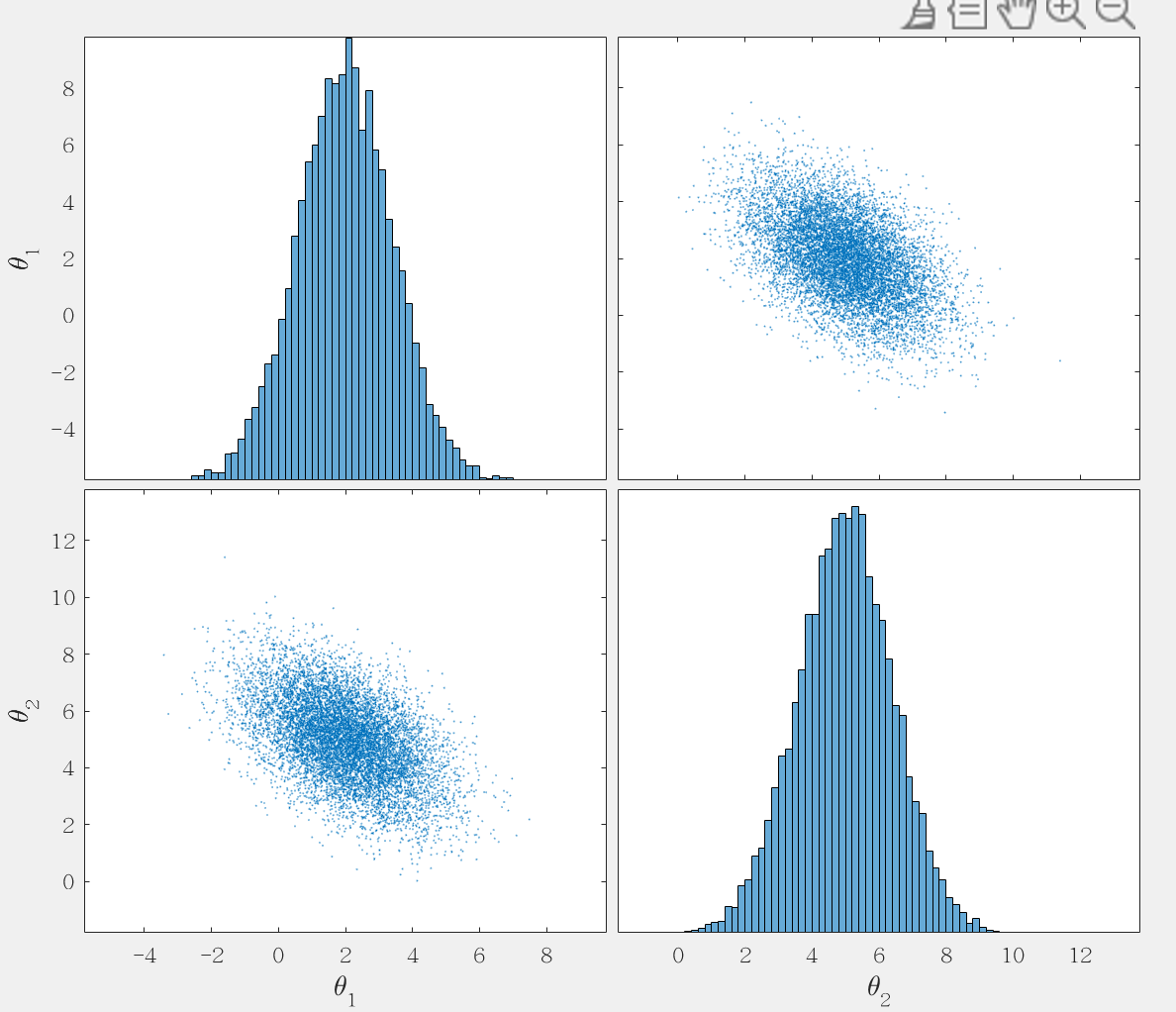
运行结果如下：