实验三

任务一

 1.作用是定义分段对应的等级，形参：整型   返回值：字符型

 2.会导致代码一直执行，无法终止。

task2

1.通过对某一数的各位取余数，使得最后的结果为该数各位上数字之和。

2.可以，新改后用的是递归的方法，将多位数递归分解。 

 

task3

1.如果n=0，则会输出1（也许需要考虑x!=0）如果n是奇数，则改为算x*x的n-1次方。如果n是偶数，n/2则会一直递归到1,1在递归到0，则是x的（n/2）次方的平方。输出结果是x的n次方。

2.是，递归模式见上述。

task4

 

#include<stdio.h>
#include<math.h>
int is_prime(int n);
int main(){
    int count=0;
    printf("100以内的孪生素数:\n");
    for(int n=2;n<=98;n++){
        if(is_prime(n)&&is_prime(n+2)){
            printf("%d%d\n"n,n+2);
            count++
        }
    }
    printf("100以内的孪生素数共有%d个。\n",count);
    return 0;
}
int is_prime(int n){
    int i,k;
    k=sqrt(1.0*x);
    for(i=2;i<=k;k++){
        if(x%i==0){
            return 0;
        }
    }
    return 1;
}

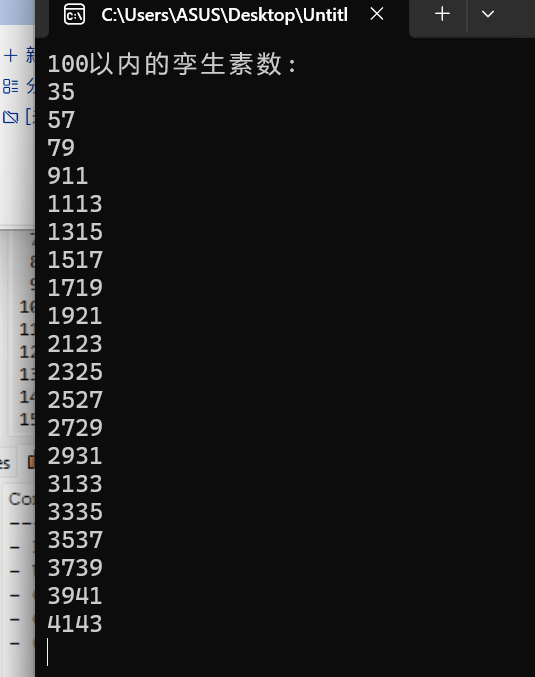
有问题

task5

 

 #include <stdio.h>
 int func(int n, int m);
 
int main() {
    int n, m;
    int ans;
    while(scanf("%d%d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
    }
    return 0;
}
 int func(int n, int m) {
    int egg = 1;
    for (int i = 0; i < m; i++) {
        egg *= (n - i);
    }
    int power = 1;
    for (int i = 1; i <= m; i++) {
        power *= i;
    }
    return egg / power;
}   

 #include <stdio.h>
 int func(int n, int m);
 
int main() {
    int n, m;
    int ans;
    while(scanf("%d%d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
    }
    return 0;
}
       int func(int n, int m) {
    if (m == 0) {
        return 1;
    }
    if (m == n) {
        return 1;
    }
    return func(n - 1, m) + func(n - 1, m - 1);
}

task6

#include <stdio.h>
int gcd(int a, int b, int c);
int main() {
    int a, b, c;
    int ans;
    while( scanf("%d %d %d", &a, &b, &c)!=EOF){
    ans = gcd(a, b, c);
    printf("%d\n", ans);
}  
 return 0;
}
int gcd(int a, int b, int c) {
    int min = a;
    if (b < min) {
        min = b;
    }
    if (c < min) {
        min = c;
    }
    for (int i = min; i >= 1; i--) {
        if (a % i == 0 && b % i == 0 && c % i == 0) {
            return i;
        }
    }
    return 1;
}