图
1.学习总结(2分)
1.1图的思维导图
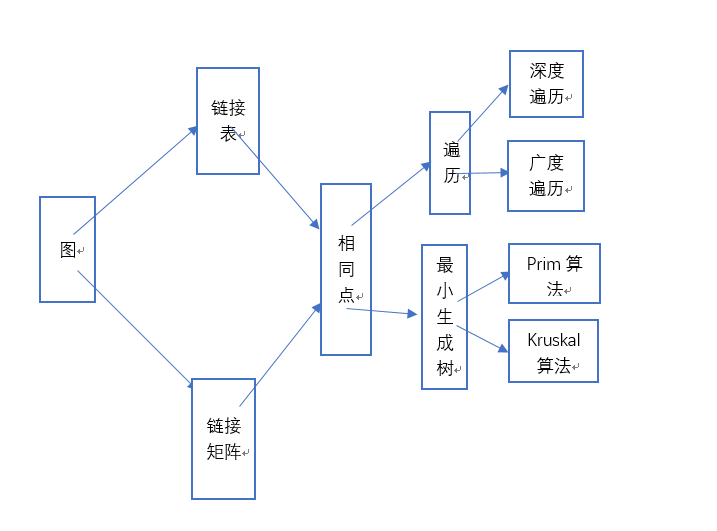
图的存储结构--图的遍历---最小生成树--最短路径---拓扑排序、关键路径,这些知识点需要都梳理。
1.2 图结构学习体会
深度遍历算法
深度遍历我的做法是采用递归算法,用一个visited数组来记录遍历过得路径,最终得到整个图的路程,它的时间复杂度为o(n平方)
广度遍历算法
广度遍历是首先访问初始顶点,然后访问定点的所有领节点,以此类推,最终可以访问整个图。以邻接表为储存结构,需要使用一个队列、
Prim和Kruscal算法
这两个算法都是用来构建最小生成树的算法,两个算法的方式不同,Kruscal算法运用到排序方面的内容,可使算法的时间复杂度更小。
Dijkstra算法
此算法是用来寻找两点之间的最短路径,其中比较特殊的就是要更新顶点到其他点的路径,会随着顶点加入s数组而是,不在数组中的顶点与初始点的距离产生变化。
拓扑排序算法
在有向图中找一个拓扑排序的过程叫做拓扑排序。
其方法为,从有向图中找度为0的顶点并输出它,然后删除该顶点和该顶点所具有的有向边,在重复以上步骤即可。
2.PTA实验作业(4分)
2.1 题目1:题目名称 六度空间(30 分)
2.2 设计思路(伪代码或流程图)
定义变量last=v,level=0,cnt=1,分别表示每层的最后一个数,层数,六层以内的个数,并进行初始化。
int visited[MAXV]来记录访问过得节点。
让初始点进队
while(队列不为空的时候){
进行广度遍历
在遍历中
if(!visit[i])在这个带你没有访问过是{
cnt++
让visit[i]=1,来代表此节点已经访问
}
if(v等于last时)说明这一层已经访问完全{
level++
并更新last
}
直到level=6的时候 退出循环。
}
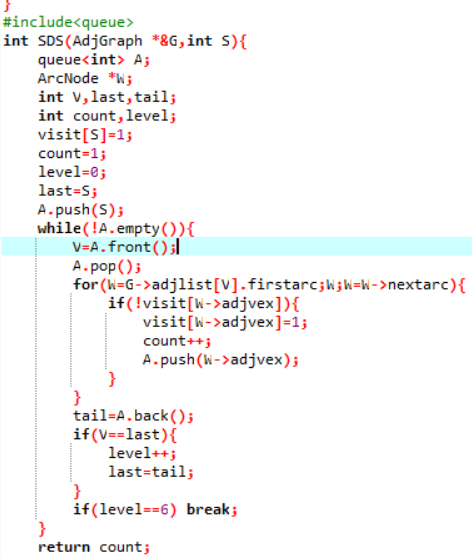
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
请贴主要函数代码,一些操作函数代码不需要贴图。
2.4 PTA提交列表说明。


这次的错误主要是因为
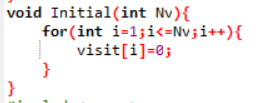
我在初始化visit函数的时候,是从0-n-1;
而我之前建图的时候是从1-n导致错误。
2.1 题目1:题目名称 7-4 公路村村通(30 分)
2.2 设计思路(伪代码或流程图)
这道题我是采用Prim算法。来得到最小生成树。
建完图后
建立两个数组low[MAXV],clost[MAXV],来记录U到V-U之间选择权值在最小的边。
for(i=0 to i<g.n){
初始化low[i]的值和clost[i]=v的值。
end for
for(i=0 to i<g.n){
定义min=INF,min用来寻找最小边的权值。
for(j=1toj<g.n){
在(V-U)中寻找距离U最近的点
并定义k来记录最近顶点的编号。
}
让k节点进入U数组中
判断图是否联通 if(min=INF)说明道路没有立联通 输出-1;
节点k进入U数组后,
图与剩下节点的距离就会改变
因此
for(j=0 to j=G.n){
if(k节点到其他节点的距离更短) 修改low数组。
}
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
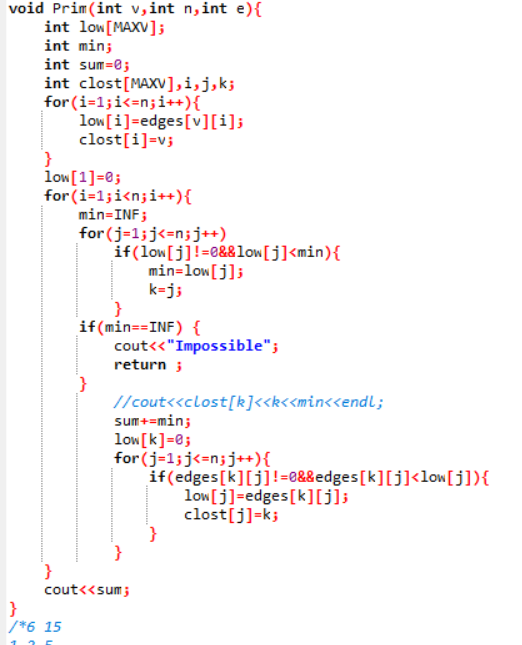
2.4 PTA提交列表说明。

这道题我是在dvc上调试好的,有以个错误是不知道如何在Prim算法中判断图是否联通,
后来军霖大佬告诉我说在寻找最小权值的for循环之后,判断min的值是否改变,如果出现min值没有改变的情况
就说明图是不通的。
2.1 题目1:题目名称 7-7 旅游规划(25 分)
2.2 设计思路(伪代码或流程图)
本题使用迪克斯拉算法来寻找最短的路径
如果不同的路径的路程相同则考虑价格的多少即可
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)


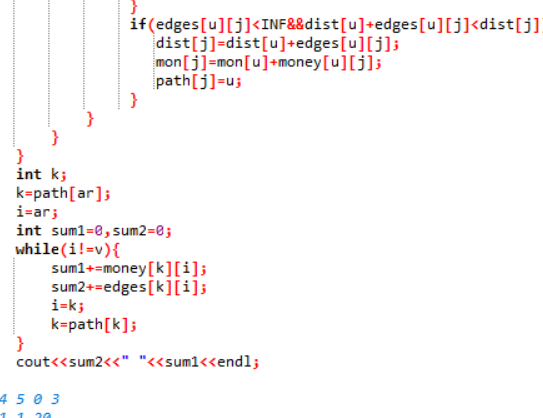
2.4 PTA提交列表说明。

3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)


出现段错误的原因是空间太大,这题我是吧结构体给取消了,设置两个全局变量edges[MAXV][AXV]和money[MAXV][MAXV];
这样就解决了段错误的原因,但是我不知道为什么会这样,可能是结构体所占的内存很大吧。
3.2 我的总分:
本题评分规则:252
4. 阅读代码(必做,1分)
3.5 关键路径的算法:
(1)输入e条弧<j,k>,建立AOE-网的存储结构;
(2)从源点v0出发,令ve[0]=0,按拓扑有序求其余各顶点的最早发生时间ve[i] (1≤i≤n-1)。如果得到的拓扑有序序列中顶点个数小于网中顶点数n,则说明网中存在环,不能求关键路径,算法终止;否则执行步骤(3)。
(3)从汇点vn出发,令vl[n-1]=ve[n-1],按逆拓扑有序求其余各顶点的最迟发生时间vl[i](n-2≥i≥0);
(4)根据各顶点的ve和vl值,求每条弧s的最早开始时间e(s)和最迟开始时间 l(s)。若某条弧满足条件e(s)=l(s),则为关键活动。
Status TopologicalOrder(ALGraph G,Stack &T){
//有向网G采用邻接表存储结构,求各顶点事件的最早发生时间ve(全局变量)。
//T为拓扑序列顶点栈,s为零入度顶点栈。若G无回路,返回G的一拓扑序列,函数值为OK,否则ERROR。
FindInDegree(G,indegree);//对各顶点求入度indegree[0..vernum-1]
for(i=0;i<G.vexnum; ++i)
if(!indegree[i])Push(S,i) //建零入度顶点栈,s入度为0者进栈
InitStack(T); count=0;ve[0..G.vexnum-1]=0; //初始化
while(!StackEmpty(S)){ //j号顶点入T栈并计数
Pop(S,j); Push(T,j);++count;
for(p=G.vertices[j].firstarc;p;p=p->nextarc){
k=p—>adjvex; //对i号顶点的每个邻接点的入度减l
if(--indegree[k]==0)Push(S,k); //若入度减为0,则入栈
if(ve[j]+*(p->info)>ve[k] ) ve[k]=ve[j]+*(p->info);
}//for *(p->info)=dut(<j,k>)
}//while
if(count<G.vexnum) return ERROR; //该有向网有回路
else return OK;
}//TopologicalOrder
Status CriticalPath (ALGraph G){ //G为有向网,输出G的各项关键活动。
if(!TopologicalOrder(G,T)) return ERROR; //初始化顶点事件的最迟发生时间
vl[0..G.vexnum-1]=ve[0..C.vexnum-1]; //按拓扑逆序求各顶点的vl值
while(!StackEmpty(T))
for( Pop(T, j), p=G.vertices[j].firstarc;p; p=p->nextarc){
k=p->adjvex; dut=*(p—>info); //dut<i,k>
if(vl[k]-dut<vl[j]) vl[j]=vl[k]-dut; }//for
for(j=0;j<G.vexnum;++j) //求ee,el和关键活动
for(p=G.vertices[j];p;p=p->nextarc){
k=p->adjvex; dut=*(p—>info);ee=ve[j];el=v1[k]-dut;tag = (ee==e1) ? ‘*’ : ‘’;
printf(j,k,dut,ee,el,tag); //输出关键活动
}
}//CriticalPath






 浙公网安备 33010602011771号
浙公网安备 33010602011771号