Introduction
生成对象(Object):对图像,视频,蛋白质等数据类型可视为向量,即 \(z \in \mathbb{R}^d\)
生成(Generation):从数据分布中采样,\(z \sim p_{data}\)
数据集(Dataset):服从数据分布的有限样本,\(z_1, ...,z_N \sim p_{data}\)
条件生成(Conditional Generation):从条件分布中采样,\(z \sim p_{data}(\cdot \mid y)\)
目标:训练生成模型,将初始分布(\(p_{\text{init}}\))的样本转化为数据分布样本\(p_{\text{data}}\)
Flow and Diffusion Models
通过模拟常微分方程(Ordinary Differential Equations, ODEs)和随机微分方程(Stochastic Differential Equations, SDEs)可以实现从初始分布到数据分布的转换,分别对应Flow Model和Diffusion Model
Flow Models
Flow Model可以由ODE来描述,即
\[X_0 \sim p_{\text{init}} \quad \triangleright \text{random init}\\
\frac{d}{dt}X_t=u_t^\theta(X_t) \quad \triangleright \text{ODE} \\
\text{Goal: } X_1 \sim p_{\text{data}} \Leftrightarrow \psi_{1}^{\theta}(X_0) \sim p_{\text{data}}
\]
其中向量场 \(u_t^\theta: \mathbb{R}^d\times[0,1] \rightarrow \mathbb{R}^d\) 为神经网络,\(\theta\)为参数。\(\psi^\theta_t\)描述了由\(u_t^\theta\)引起的Flow,为ODE方程解(Trajectory)的集合
通过使用Euler算法,可以模拟ODE计算出Flow,实现从Flow Model中采样

Diffusion Models
Diffusion Model可以由SDEs描述,如下所示(由于其随机性SDEs不使用微分表示形式)
\[dX_t = u_t^\theta(X_t)dt +\sigma_tdW_t \quad \triangleright \text{SDE} \\
X_0 \sim p_{init} \quad \triangleright \text{random initialization} \\
\text{Goal: } X_1 \sim p_{\text{data}}
\]
其中 \(\sigma_t \geq 0\)为diffusion系数,\(W_t\)为随机过程 布朗运动(Brownian motion)
可以看出Diffusion Model是Flow Model的一个拓展,当\(\sigma_t = 0\)时即为Flow Model
同样的,可以使用以下算法实现从Diffusion Model中采样

Training Target and Train Loss
对于Flow Model和Diffusion Model
\[\begin{align*}
X_0 \sim p_{\text{init}},\quad dX_t &= u_t^\theta(X_t) dt & \text{(Flow model)} \\
X_0 \sim p_{\text{init}},\quad dX_t &= u_t^\theta(X_t) dt + \sigma_t dW_t & \text{(Diffusion model)}
\end{align*}
\]
训练可以通过最小化以下损失实现
\[\mathcal{L}(\theta) = \left\| u_t^\theta(x) - \underbrace{u_t^{\text{target}}(x)}_{\text{training target}} \right\|^2
\]
\(u_t^\theta\) 为网络模型,\(u_t^{\text{target}}(x)\)为目标向量场,其实现将初始数据分布转化为目标数据分布,为了实现计算 \(\mathcal{L}(\theta)\) 或者间接计算 \(\mathcal{L}(\theta)\)需要构建\(u_t^{\text{target}}(x)\)。
Probability Path
Probability Path是从初始分布到目标数据分布的渐进插值(gradual interpolation),分为条件概率路径(conditional probability path)和边缘概率路径(marginal probability path),分别为\(p_t(\cdot \mid z)\) 和 \(p_t(\cdot)\),其中:
\[p_0(\cdot \mid z) = p_{\text{init}}, \quad p_1(\cdot \mid z) = \delta_z \quad \text{for all } z \in \mathbb{R}^d
\]
\(p_t(\cdot)\) 可由以下公式获得
\[\begin{align*}
&z \sim p_{\text{data}},\ x \sim p_t(\cdot \mid z) \implies x \sim p_t &\triangleright \text{sampling from marginal path} \\
&p_t(x) = \int p_t(x \mid z) p_{\text{data}}(z)dz &\triangleright \text{density of marginal path} \\
&p_0 = p_{\text{init}} \quad \text{and} \quad p_1 = p_{\text{data}}
&\triangleright \text{noise-data interpolation} \\
\end{align*}
\]
Training Target for Flow Model
对于\(z \in \mathbb{R^d} \sim p_{data}\),记\(u_t^{target}(\cdot \mid z)\)为条件概率路径 \(p_t(\cdot \mid z)\) 对应的条件向量场,即
\[X_0 \sim p_{\text{init}},\quad \frac{\mathrm{d}}{\mathrm{d}t}X_t = u_t^{\text{target}}(X_t|z) \quad \Rightarrow \quad X_t \sim p_t(\cdot|z) \quad (0 \leq t \leq 1)
\]
则\(u_t^{target}(x)\)可定义为
\[u_t^{\text{target}}(x) = \int u_t^{\text{target}}(x|z) \frac{p_t(x|z)p_{\text{data}}(z)}{p_t(x)} \,\mathrm{d}z
\]
且满足:
\[X_0 \sim p_{\text{init}},\quad \frac{\mathrm{d}}{\mathrm{d}t}X_t = u_t^{\text{target}}(X_t) \quad \Rightarrow \quad X_t \sim p_t \quad (0 \leq t \leq 1)
\]
其中\(X_1 \sim p_{data}\)。
这可以由Continuity Equation 证明
Continuity Equation
对于向量场\(u_t^{target}\) 且 \(X_0 \sim p_{init}\),有\(X_t \sim p_t\) 在\(0 \leq t \leq 1\) 成立有且仅有
\[\partial_t p_t(x) = -\mathrm{div}(p_t u_t^{\text{target}})(x) \quad \text{for all } x \in \mathbb{R}^d, 0 \leq t \leq 1
\]
其中\(\partial_t p_t(x) = \frac{\mathrm{d}}{\mathrm{d}t} p_t(x)\),\(\mathrm{div}(v_t)(x) = \sum_{i=1}^d \frac{\partial}{\partial x_i} v_t(x)\)
Training Target for Diffusion Model
同样的,对于Diffusion Model,可以构建\(u_t^{target}\)如下所示,满足\(X_t \sim p_t \quad (0 \leq t \leq 1)\) ,即
\[\begin{align*}
&X_0 \sim p_{\text{init}}, \quad \mathrm{d}X_t = \left[ u_t^{\text{target}}(X_t) + \frac{\sigma_t^2}{2} \nabla \log p_t(X_t) \right] \mathrm{d}t + \sigma_t \mathrm{d}W_t \\
&\Rightarrow X_t \sim p_t \quad (0 \leq t \leq 1)
\end{align*}
\]
并且将\(p_t(x), u_t^{target}\) 替换为 \(p_t(x\mid z), u_t^{target}(x \mid z)\) 时仍然成立
其中,\(\nabla \log p_t(x)\) 称为marginal score function,\(\nabla \log p_t(x \mid z)\) 称为conditional score function,二者满足
\[\nabla \log p_t(x) = \frac{\nabla p_t(x)}{p_t(x)} = \frac{\nabla \int p_t(x|z) p_{\text{data}}(z) \,\mathrm{d}z}{p_t(x)} = \frac{\int \nabla p_t(x|z) p_{\text{data}}(z) \,\mathrm{d}z}{p_t(x)} = \int \nabla \log p_t(x|z) \frac{p_t(x|z) p_{\text{data}}(z)}{p_t(x)} \,\mathrm{d}z
\]
这可以由Fokker-Planck Equation证明
Fokker-Planck Equation
对于\(X_0 \sim p_{\text{init}}, \quad \mathrm{d}X_t = u_t(X_t)\,\mathrm{d}t + \sigma_t\,\mathrm{d}W_t\) 描述的SDE,\(X_t \sim p_t\) 成立,当且仅当
\[\partial_t p_t(x) = -\mathrm{div}(p_t u_t)(x) + \frac{\sigma_t^2}{2} \Delta p_t(x) \quad \text{for all } x \in \mathbb{R}^d, 0 \leq t \leq 1
\]
其中,\(\Delta w_t(x) = \sum_{i=1}^d \frac{\partial^2}{\partial x_i^2} w_t(x) = \mathrm{div}(\nabla w_t)(x)\)
Remark Langevin dynamics
当\(p_t=p\)时,即概率路径为静态时,有
\[\mathrm{d}X_t = \frac{\sigma_t^2}{2} \nabla \log p(X_t)\,\mathrm{d}t + \sigma_t\,\mathrm{d}W_t
\]
此时 \(X_0 \sim p \quad \Rightarrow \quad X_t \sim p \quad (t \geq 0)\),即Langevin dynamics
Gaussian probability path
设噪声调度\(\alpha_t, \beta_t\)为单调连续可微函数且\(\alpha_0=\beta_1=0, \alpha_1=\beta_0=1\),定义Gaussian conditional probability path为
\[p_t(\cdot|z) = \mathcal{N}(\alpha_t z, \beta_t^2 I_d)
\]
其满足 \(p_0(\cdot|z) = \mathcal{N}(\alpha_0 z, \beta_0^2 I_d) = \mathcal{N}(0, I_d), \quad \text{and} \quad p_1(\cdot|z) = \mathcal{N}(\alpha_1 z, \beta_1^2 I_d) = \delta_z\)
则从其marginal path中采样可以通过以下方法得到
\[z \sim p_{\text{data}},\ \epsilon \sim p_{\text{init}} = \mathcal{N}(0, I_d) \Rightarrow x = \alpha_t z + \beta_t \epsilon \sim p_t
\]
基于Gaussian probability path的conditional Gaussian vector field可以计算得到
\[u_t^{\text{target}}(x|z) = \left( \dot{\alpha}_t - \frac{\dot{\beta}_t}{\beta_t} \alpha_t \right) z + \frac{\dot{\beta}_t}{\beta_t} x
\]
其中\(\dot{\alpha}_t = \partial_t \alpha_t\),\(\dot{\beta}_t = \partial_t \beta_t\)
同样的可以得到其marginal score function为
\[\nabla \log p_t(x|z) = -\frac{x - \alpha_t z}{\beta_t^2}
\]
Flow Matching
对于Flow Model,定义flow matching loss为
\[\begin{align*}
\mathcal{L}_{\text{FM}}(\theta) &= \mathbb{E}_{t \sim \text{Unif}, x \sim p_t}[\|u_t^\theta(x) - u_t^{\text{target}}(x)\|^2] \\
&= \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, x \sim p_t(\cdot|z)}[\|u_t^\theta(x) - u_t^{\text{target}}(x)\|^2]
\end{align*}
\]
\(z \sim p_{\text{data}},\ x \sim p_t(\cdot \mid z) \implies x \sim p_t\)
定义conditional flow matching loss为
\[\mathcal{L}_{\text{CFM}}(\theta) = \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, x \sim p_t(\cdot|z)}[\|u_t^\theta(x) - u_t^{\text{target}}(x|z)\|^2]
\]
其中\(u_t^{\text{target}}(x|z)\)可以人为构造获得(例如Gaussian probability path)
可以证明,
\[\mathcal{L}_{\text{FM}}(\theta) = \mathcal{L}_{\text{CFM}}(\theta) + C
\]
即
\[\nabla_\theta \mathcal{L}_{\text{FM}}(\theta) = \nabla_\theta \mathcal{L}_{\text{CFM}}(\theta)
\]
因此优化\(\mathcal{L}_{\text{CFM}}\)即优化\(\mathcal{L}_{\text{FM}}\),而对于\(\mathcal{L}_{\text{CFM}}\),只需构造probability path即可,至此可以得到训练Flow Model的算法,整个流程即称为Flow Matching
Flow Matching for Gaussian Conditional Probability Paths
对于Gaussian Probability Path,有
\[\epsilon \sim \mathcal{N}(0, I_d) \quad \Rightarrow \quad x_t = \alpha_t z + \beta_t \epsilon \sim \mathcal{N}(\alpha_t z, \beta_t^2 I_d) = p_t(\cdot|z)
\]
\[u_t^{\mathrm{target}}(x|z)=\left(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\right)z+\frac{\dot{\beta}_t}{\beta_t}x
\]
\[\begin{gathered}
\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_{\mathrm{data}},x\sim\mathcal{N}(\alpha_{t}z,\beta_{t}^{2}I_{d})}[\|u_{t}^{\theta}(x)-\left(\dot{\alpha}_{t}-\frac{\dot{\beta}_{t}}{\beta_{t}}\alpha_{t}\right)z-\frac{\dot{\beta}_{t}}{\beta_{t}}x\|^{2}] \\
\overset{(i)}{\operatorname*{=}}\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_{\mathrm{data}},\epsilon\sim\mathcal{N}(0,I_{d})}[\|u_{t}^{\theta}(\alpha_{t}z+\beta_{t}\epsilon)-(\dot{\alpha}_{t}z+\dot{\beta}_{t}\epsilon)\|^{2}]
\end{gathered}
\]
特别的,对于\(\alpha_t=t\),\(\beta_t=1-t\),有
\[p_{t}(x|z)=\mathcal{N}(tz,(1-t)^{2})
\]
\[\mathcal{L}_{\mathrm{cfm}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_{\mathrm{data}},\epsilon\sim\mathcal{N}(0,I_{d})}[\|u_{t}^{\theta}(tz+(1-t)\epsilon)-(z-\epsilon)\|^{2}]
\]
称之为(Gaussian) CondOT probability path,训练过程如下所示

Score Matching
对于Diffusion Models,由于\(u_t^{target}\) 难以得到,因此使用score network \(\sigma_t^2 : \mathbb{R}^d \times [0, 1] \to \mathbb{R}\)对score function进行拟合,同样的,存在score matching loss和conditional score matching loss如下
\[\begin{align*}
\mathcal{L}_{\text{SM}}(\theta) &= \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, x \sim p_t(\cdot|z)}[\|s_t^\theta(x) - \nabla \log p_t(x)\|^2] \quad \triangleright \text{ score matching loss} \\
\mathcal{L}_{\text{CSM}}(\theta) &= \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, x \sim p_t(\cdot|z)}[\|s_t^\theta(x) - \nabla \log p_t(x|z)\|^2] \quad \triangleright \text{ conditional score matching loss}
\end{align*}
\]
同样的,虽然\(\nabla \log p_t(x)\)未知,但\(\nabla \log p_t(x \mid z)\)可以人工构造,且存在
\[\begin{align*}
&\mathcal{L}_{\text{SM}}(\theta) = \mathcal{L}_{\text{SFM}}(\theta) + C \\
&\implies \nabla_\theta \mathcal{L}_{\text{SM}}(\theta) = \nabla_\theta \mathcal{L}_{\text{CSM}}(\theta)
\end{align*}
\]
因此,优化\(\mathcal{L}_{\text{CSM}}(\theta)\)即可,此时采样过程如下所示
\[X_0 \sim p_{\text{init}}, \quad \mathrm{d}X_t = \left[ u_t^\theta(X_t) + \frac{\sigma_t^2}{2} s_t^\theta(X_t) \right] \mathrm{d}t + \sigma_t \mathrm{d}W_t \implies X_1 \sim p_{data}
\]
其中,尽管理论上对任意\(\sigma_t \geq 0\)均可实现采样,但由于存在对随机微分方程模拟不精确导致的精度误差,以及训练误差,因此存在一个最优的\(\sigma_t\)。同时观察采样过程可以发现模拟该SDE还需学习\(u_t^\theta\),但其实通常可以使用一个两输出的网络同时处理\(u_t^\theta\)和\(s_t^\theta\),并且对于特定的概率路径,两者可以相互转化。
Denoising Diffusion Models: Score Matching for Gaussian Probability Paths
对于Gaussian Probability Paths,有
\[\nabla \log p_t(x|z) = -\frac{x - \alpha_t z}{\beta_t^2}
\]
则
\[\begin{align*}
\mathcal{L}_{\text{CSM}}(\theta) &= \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, x \sim p_t(\cdot|z)}\left[\left\|s_t^\theta(x) + \frac{x - \alpha_t z}{\beta_t^2}\right\|^2\right] \\
&= \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, \epsilon \sim \mathcal{N}(0, I_d)}\left[\left\|s_t^\theta(\alpha_t z + \beta_t \epsilon) + \frac{\epsilon}{\beta_t}\right\|^2\right] \\
&= \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, \epsilon \sim \mathcal{N}(0, I_d)}\left[\frac{1}{\beta_t^2} \left\|\beta_t s_t^\theta(\alpha_t z + \beta_t \epsilon) + \epsilon\right\|^2\right]
\end{align*}
\]
由于\(\frac{1}{\beta^2_t}\)在\(\beta_t\)趋近于0时loss趋近于无穷大,因此通常舍弃常数项\(\frac{1}{\beta^2_t}\),并用以下方法reparameterize \(s^\theta_t\)为\(\epsilon_t^\theta\)(噪声预测网络)得到DDPM损失函数
\[-\beta_t s_t^\theta(x) = \epsilon_t^\theta(x) \quad \Rightarrow \quad \mathcal{L}_{\text{DDPM}}(\theta) = \mathbb{E}_{t \sim \text{Unif}, z \sim p_{\text{data}}, \epsilon \sim \mathcal{N}(0, I_d)}\left[\left\|\epsilon_t^\theta(\alpha_t z + \beta_t \epsilon) - \epsilon\right\|^2\right]
\]
其训练过程如下所示

此外,对于Gaussian Probability Paths,vector field和score可以相互转化,即
\[u_t^{\text{target}}(x|z) = \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) \nabla \log p_t(x|z) + \frac{\dot{\alpha}_t}{\alpha_t} x \\
u_t^{\text{target}}(x) = \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) \nabla \log p_t(x) + \frac{\dot{\alpha}_t}{\alpha_t} x
\]
proof
\[u_t^{\text{target}}(x|z) = \left( \dot{\alpha}_t - \frac{\dot{\beta}_t}{\beta_t} \alpha_t \right) z + \frac{\dot{\beta}_t}{\beta_t} x
\stackrel{(i)}{=} \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) \left( \frac{\alpha_t z - x}{\beta_t^2} \right) + \frac{\dot{\alpha}_t}{\alpha_t} x
= \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) \nabla \log p_t(x|z) + \frac{\dot{\alpha}_t}{\alpha_t} x
\]
\[\begin{align*}
u_t^{\text{target}}(x) &= \int u_t^{\text{target}}(x|z) \frac{p_t(x|z) p_{\text{data}}(z)}{p_t(x)} \,\mathrm{d}z \\
&= \int \left[ \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) \nabla \log p_t(x|z) + \frac{\dot{\alpha}_t}{\alpha_t} x \right] \frac{p_t(x|z) p_{\text{data}}(z)}{p_t(x)} \,\mathrm{d}z \\
&\stackrel{(i)}{=} \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) \nabla \log p_t(x) + \frac{\dot{\alpha}_t}{\alpha_t} x
\end{align*}
\]
\(u_t^\theta\)和\(s^\theta_t\) 也可以相互转化,有
\[u_t^\theta(x) = \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t \right) s_t^\theta(x) + \frac{\dot{\alpha}_t}{\alpha_t} x
\]
\[s_t^\theta(x) = \frac{\alpha_t u_t^\theta(x) - \dot{\alpha}_t x}{\beta_t^2 \alpha_t - \alpha_t \dot{\beta}_t \beta_t}
\]
因此对于Gaussian probability paths来说,只需训练\(u_t^\theta\)或\(s^\theta_t\) 即可,且使用flow matching或者使用score matching的方法均可
最后,对于训练好的\(s_t^\theta\) 从SDE中采样过程如下
\[X_0 \sim p_{\text{init}}, \quad \mathrm{d}X_t = \left[ \left( \beta_t^2 \frac{\dot{\alpha}_t}{\alpha_t} - \dot{\beta}_t \beta_t + \frac{\sigma_t^2}{2} \right) s_t^\theta(x) + \frac{\dot{\alpha}_t}{\alpha_t} x \right] \mathrm{d}t + \sigma_t \mathrm{d}W_t \\
\implies X_1=p_{data}
\]
Summary
总的来说,Flow Matching比Score Matching更简洁并且Flow Matching更具有拓展性,可以实现从一个任意初始分布\(p_{init}\)得到任意分布\(p_{data}\),但是denoising diffusion models只适用于Gaussian initial distributions and Gaussian probability path。Flow Matching类似于Stochastic Interpolants。
Conditional (Guided) Generation
在给定条件下进行生成(generate an object conditioned on some additional information),称之为conditional generation,为了和conditional vector field区分多称为guided generation
用数学语言描述即,对于\(y \in \mathcal{Y}\),对\(p_{data}(x \mid y)\)中采样,因此模型包含条件向量场\(u_t^{\theta}(\cdot \mid y)\),模型架构如下所示
\[\begin{align*}
\text{Neural network: } & u_t^\theta : \mathbb{R}^d \times \mathcal{Y} \times [0, 1] \to \mathbb{R}^d, \quad (x, y, t) \mapsto u_t^\theta(x|y) \\
\text{Fixed: } & \sigma_t : [0, 1] \to [0, \infty), \quad t \mapsto \sigma_t
\end{align*}
\]
对于给定的\(y \in \mathbb{R}^{d_y}\),采样过程可以描述为
\[\begin{align*}
\text{Initialization:} \quad & X_0 \sim p_{\text{init}} \quad &\triangleright \text{ Initialize with simple distribution} \\
\text{Simulation:} \quad & \mathrm{d}X_t = u_t^\theta(X_t|y)\,\mathrm{d}t + \sigma_t\,\mathrm{d}W_t \quad &\triangleright \text{ Simulate SDE from } t=0 \text{ to } t=1. \\
\text{Goal:} \quad & X_1 \sim p_{\text{data}}(\cdot|y) \quad &\triangleright X_1 \text{ to be distributed like } p_{\text{data}}(\cdot|y)
\end{align*}
\]
上述在\(\sigma_t=0\)时即为guided flow model
Guided Models
Guided Flow Models的训练损失(优化目标,或者说guided conditional flow matching objective)很容的得到,如下所示
\[\begin{align*}
\mathcal{L}_{\text{CFM}}^{\text{guided}}(\theta) &= \mathbb{E}_{(z,y) \sim p_{\text{data}}(z,y),\, t \sim \text{Unif}(0,1),\, x \sim p_t(\cdot|z)} \left[ \left\| u_t^\theta(x|y) - u_t^{\text{target}}(x|z) \right\|^2 \right]
\end{align*}
\]
同样的,对于Guided Diffusion Models,有guided conditional score matching objective如下
\[\begin{align*}
\mathcal{L}_{\text{CSM}}^{\text{guided}}(\theta) &= \mathbb{E}_{\square} \left[ \| s_t^\theta(x|y) - \nabla \log p_t(x|z) \|^2 \right] \\
\square &= (z, y) \sim p_{\text{data}}(z, y),\ t \sim \text{Unif}(0,1),\ x \sim p_t(\cdot|z)
\end{align*}
\]
虽然理论上上述以及足够生成标签\(y\)对应样本,但是实际上生成效果并不十分fit \(y\),以及,无法控制生成内容对label的fit程度。一种解决方法是人为加强\(y\)的作用,比较先进的技术是Classifier-Free Guidance。
Classifier-Free Guidance
对于Flow Models,以Gaussian probability paths为例
\[\begin{align*}
u_t^{\text{target}}(x|y) = a_t x + b_t \nabla \log p_t(x|y)
\end{align*}
\]
其中
\[\begin{align*}
(a_t, b_t) = \left( \frac{\dot{\alpha}_t}{\alpha_t}, \frac{\dot{\alpha}_t \beta_t^2 - \dot{\beta}_t \beta_t \alpha_t}{\alpha_t} \right)
\end{align*}
\]
又
\[\begin{align*}
\nabla \log p_t(x|y) = \nabla \log \left( \frac{p_t(x) p_t(y|x)}{p_t(y)} \right) = \nabla \log p_t(x) + \nabla \log p_t(y|x)
\end{align*}
\]
则
\[\begin{align*}
u_t^{\text{target}}(x|y) = a_t x + b_t (\nabla \log p_t(x) + \nabla \log p_t(y|x)) = u_t^{\text{target}}(x) + b_t \nabla \log p_t(y|x)
\end{align*}
\]
可以看出,guided vector field是由unguided vector field和guided score相加得到,一种很自然的想法是对guided score进行加权,得到
\[\begin{align*}
\tilde{u}_t(x|y) = u_t^{\text{target}}(x) + wb_t \nabla \log p_t(y|x)
\end{align*}
\]
其中guided score可以看作是噪声类别分类器,早期的工作确实使用这样的方法实现,但是进一步对guided score进行分析得到如下:
\[\begin{align*}
\tilde{u}_t(x|y) &= u_t^{\text{target}}(x) + w_b \nabla \log p_t(y|x) \\
&= u_t^{\text{target}}(x) + w_b (\nabla \log p_t(x|y) - \nabla \log p_t(x)) \\
&= u_t^{\text{target}}(x) - (w_a x + w_b \nabla \log p_t(x)) + (w_a x + w_b \nabla \log p_t(x|y)) \\
&= (1 - w) u_t^{\text{target}}(x) + w u_t^{\text{target}}(x|y).
\end{align*}
\]
即\(\tilde{u}_t(x|y)\)由unguided vector field和guided vector field加权得到,并且,通过构造\(y = \varnothing\)其对应概率为人为设计的超参数\(\eta\),从而实现使用\(u_t^{\text{target}}(x|\varnothing)\)代替\(u_t^{\text{target}}(x)\),具体可公式化描述为
\[\begin{align*}
\mathcal{L}_{\text{CFM}}^{\text{CFG}}(\theta) &= \mathbb{E}_{\square} \left[ \| u_t^\theta(x|y) - u_t^{\text{target}}(x|z) \|^2 \right] \\
\square &= (z, y) \sim p_{\text{data}}(z, y),\ t \sim \text{Unif}(0,1),\ x \sim p_t(\cdot|z),\ \text{replace } y = \varnothing \text{ with prob. } \eta
\end{align*}
\]
对于Diffusion Models,\(\tilde{s}_t(x|y)\)同样可改写如下
\[\begin{align*}
\tilde{s}_t(x|y) &= \nabla \log p_t(x) + w \nabla \log p_t(y|x) \\
&= \nabla \log p_t(x) + w (\nabla \log p_t(x|y) - \nabla \log p_t(x)) \\
&= (1 - w) \nabla \log p_t(x) + w \nabla \log p_t(x|y) \\
&= (1 - w) \nabla \log p_t(x|\varnothing) + w \nabla \log p_t(x|y)
\end{align*}
\]
training objective如下
\[\begin{align*}
\mathcal{L}_{\text{CSM}}^{\text{CFG}}(\theta) &= \mathbb{E}_{\square} \left[ \| s_t^\theta(x|(1 - \xi)y + \xi \varnothing) - \nabla \log p_t(x|z) \|^2 \right] \\
\square &= (z, y) \sim p_{\text{data}}(z, y),\ t \sim \text{Unif}(0,1),\ x \sim p_t(\cdot|z),\ \text{replace } y = \varnothing \text{ with prob. } \eta
\end{align*}
\]
训练时,我们通常也可同时优化\({s}_t^\theta(x|y)\)和\({u}_t^\theta(x|y)\),对应的,有
\[\begin{align*}
\tilde{s}_t^\theta(x|y) &= (1 - w) s_t^\theta(x|\varnothing) + w s_t^\theta(x|y), \\
\tilde{u}_t^\theta(x|y) &= (1 - w) u_t^\theta(x|\varnothing) + w u_t^\theta(x|y).
\end{align*}
\]
采样时,有
\[\mathrm{d}X_t = \left[ \tilde{u}_t^\theta(X_t|y) + \frac{\sigma_t^2}{2} s_t^\theta(X_t|y) \right] \mathrm{d}t + \sigma_t \mathrm{d}W_t
\]
Network architectures
网络模型的设计随建模数据的复杂程度各有差别,但都需满足
\[\text{Neural network: } u_t^\theta : \mathbb{R}^d \times \mathcal{Y} \times [0, 1] \to \mathbb{R}^d, \quad (x, y, t) \mapsto u_t^\theta(x|y)
\]
U-Nets
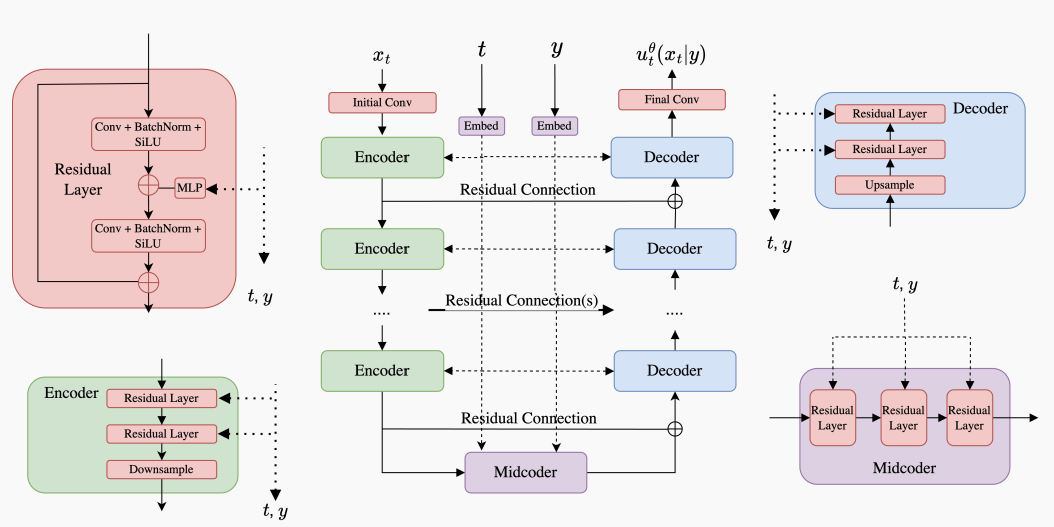
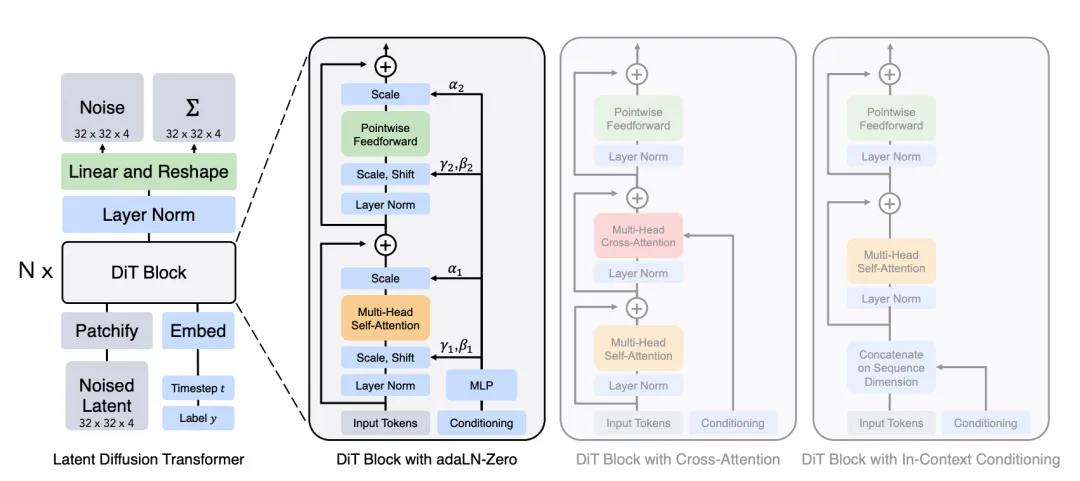
References
[1] Peter Holderrieth and Ezra Erives.An Introduction to Flow Matching and Diffusion Models[EB/OL].https://arxiv.org/abs/2506.02070,2025.
Time waits for no one.









 浙公网安备 33010602011771号
浙公网安备 33010602011771号