关系代数

概述

选择( \(\sigma\) ), 投影( \(\Pi\) ), 笛卡尔积( \(\times\) ), 连接( \(\Join_{\theta}\) ), 集合运算, 更名( \(\rho\) ),

• 是一种抽象的语言，是学习数据库语言的基础
• 关系代数运算三要素
  • 输入：一个或多个关系
  • 输出：一个新的关系
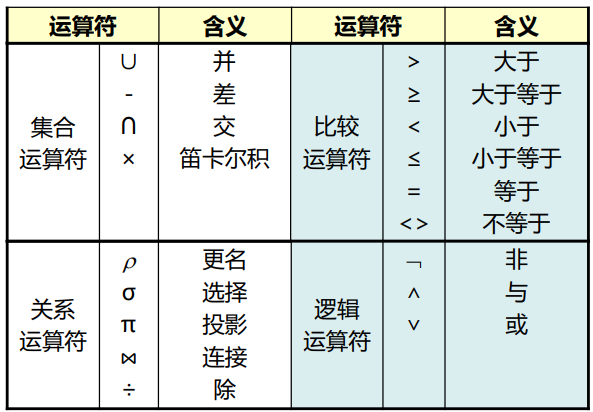
  • 运算符：四类
    • 集合运算符 - 从关系的执行角度来进行
    • 关系运算符 - 不仅涉及行而且涉及列
    • 算术比较符 - 辅助关系运算符进行操作
    • 逻辑运算符 - 辅助关系运算符进行操作

关系代数运算的分类

• 集合运算: 并、差、交、笛卡尔积
• 关系运算：更名、选择、投影、连接、除

基本运算

并, 交, 差

• 并相容性
  • 参与运算的两个关系及其相关属性之间有一定的对应性、可比性或意 义关联性
  • 定义：关系 R 与关系 S 存在相容性，当且仅当：
    • R 和 S 的属性数目必须相同；
    • 对于任意 i， R 的第 i 个属性的域必须和 S 的第 i 个属性的域相同

假设： R(A1, A2, … , An) , S(B1, B2, … ,Bm)
R和S满足并相容性： n = m 并且 Domain(Ai) = Domain(Bi)
Student(SID char(10), Sname char(8), Age char(3))
Proffessor(PID char(10), Pname char(8), Age char(3))

笛卡尔积(Cartesian-Product)

• 定义：由关系R与关系S的元组进行所有可能的拼接构成
• 数学描述： \(R × S =\{ tq | t ∈ R and q ∈ S \}\)，其中t、q是 元组
• 前提：假设R和S的属 性是不相交的，如果有相交的属性，必须通过更名(renaming)使其不相交。

更名(Rename)

• 定义：给关系或表达式重新命名
• 数学描述：
  • (1) \(ρ_X (E)\)，表示表达式E更名为X。
  • (2) \(ρ_{X(A1 , A2 , …, An )} (E)\)，表示关系E更名为X，其中的n个属性依 次更名为A1 , A2 , …, An

选择(Select)

• 定义：给定一个关系R和一个选择的条件(con), 选择运算从关 系R中选择出满足给定条件con的元组。

• 数学描述：

\[\sigma_{con}(R) = \{t | t ∈ R and con(t) == 1\} \]

• 设\(R(A_1 ,A_2 , … ,A_n )\), t是R的元组，则\(t[A_i]\)表示t的分量，con 由逻辑运算符连接比较表达式组成

• eg \(S(Name, Age, Gender)\)
  查询年龄不小于20的男学生

\[ \sigma_{Age\ge20 \wedge Gender='M'} (S) \]

投影(Project)

• 定义：指从关系R中选出若干列构成新的关系(选择列去掉重复项)

• 数学描述：\(\Pi_{A_1, A_2, …, A_n}(R)= \{ | t ∈ R \}\)

因为关系是一个集合，需要删除重复的行(新投影的关系可能有重复行)

示例：\(S(Name, Age, Gender)\)
查询所有学生的姓名和年龄

\[\Pi_{Name, Age}(S) \]

投影结合选择操作

• 先选择再投影
• 先投影再选择

附加运算

连接: 多个表进行操作

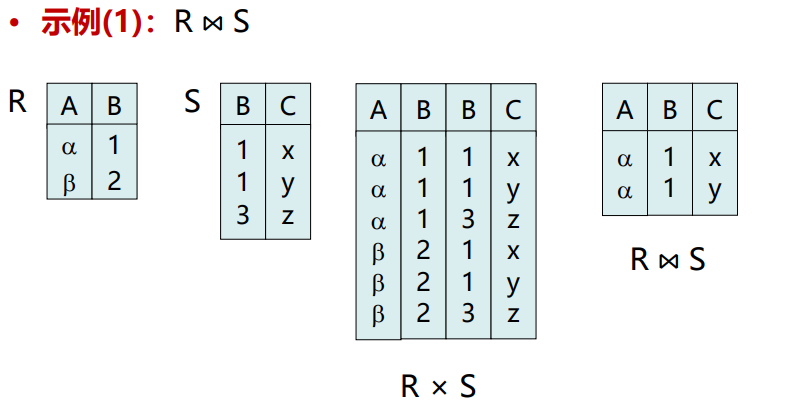
自然连接(Natural Join)

将具有相同属性的表拼接

• 定义：由关系R和关系S的笛卡尔积中选取相同属性组上值相等的元组所构成
• 数学描述：假设\(R ∩ S = {A_1 , A_2 , …, A_n }\)
  \(R \Join S = \Pi_{R∪S }(\sigma_{R.A_1=S.A_1 ∧ R.A_2=S.A_2 ∧ … ∧ R.A_n=S.A_n} (R×S)\)
  如果\(R ∩ S = ϕ\)，则\(R \Join S = R×S\)
• 注意：要在结果中去掉重复的属性列

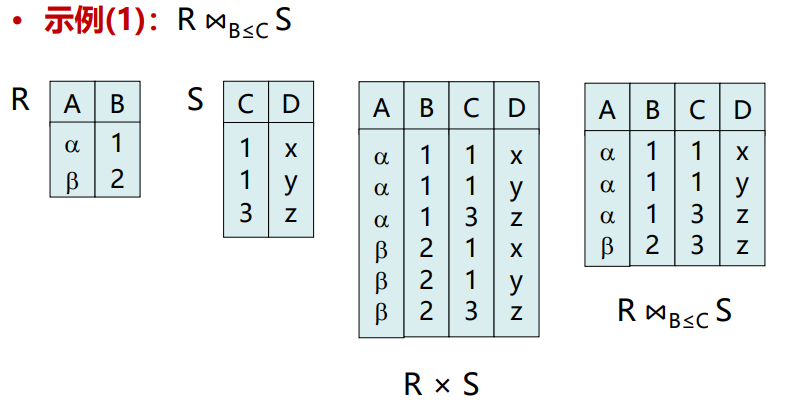
θ连接(θ-Join/ Theta Join)

• 是自然连接的扩展
• 定义：从两个关系的笛卡尔积中选取属性间满足一定条件的元组
• 数学描述：\(R \Join_{\theta} S = \sigma_{\theta} (R×S)\) ，是将一个选择运算和一个笛 卡儿乘积运算合并为的单独一个运算

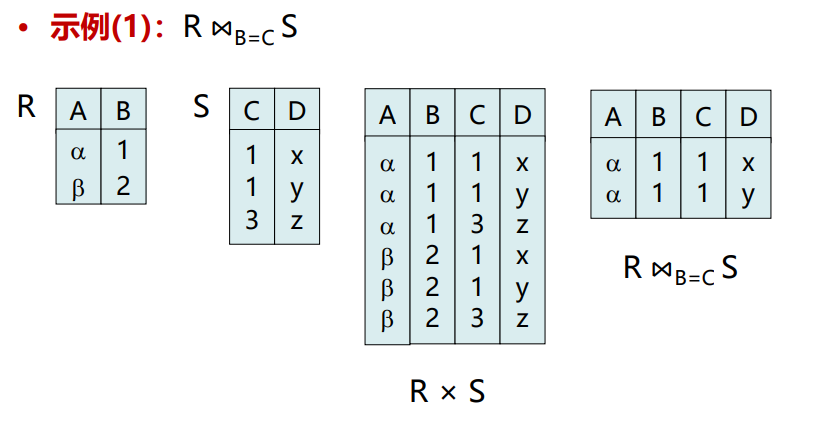
等值连接

• 定义：由关系R和关系S的笛卡尔积中选取R中属性A与S中属 性B上值相等的元组所构成
• 数学描述：\(R ⋈_{A=B} S = \theta_{t[A] = q[B]}(R×S)\) ， 即：θ连接中运算符为=时， θ连接就成为等值连接。

等值连接与自然连接

• 等值连接中不要求相等属性值的属性名相同，而自然连接要 求相等属性值的属性名必须相同，即两关系只有在同名属性 才能进行自然连接。
• 等值连接不将重复属性去掉，而自然连接去掉重复属性，也 可以说，自然连接是去掉重复列的等值连接。?

除(Division)

数学描述：R ÷ S = { t | t ∈ \(\Pi_{R-S}\)(R) and ∀u ∈ S (tu∈ R)}

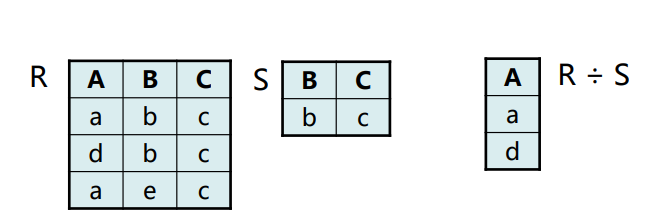
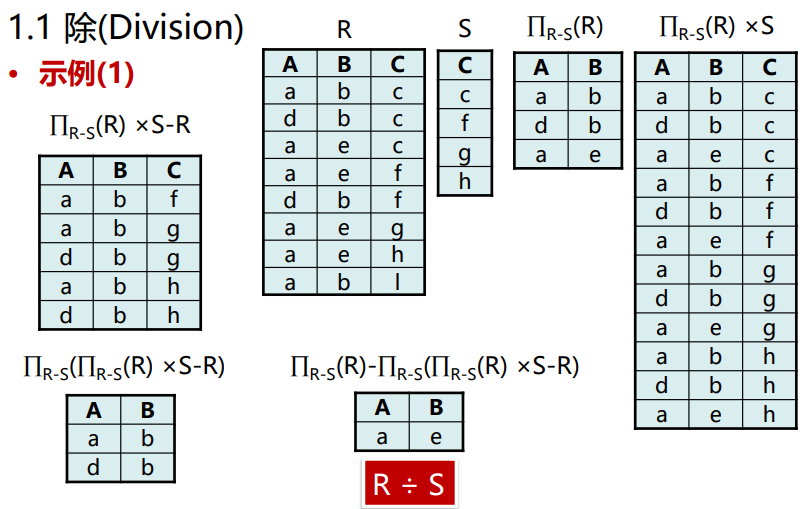
特点

• 行和列同时操作
• 常用于表达包含"对所有的(for all)" 的查询

外连接(Outer-Join)
表拼接拓展

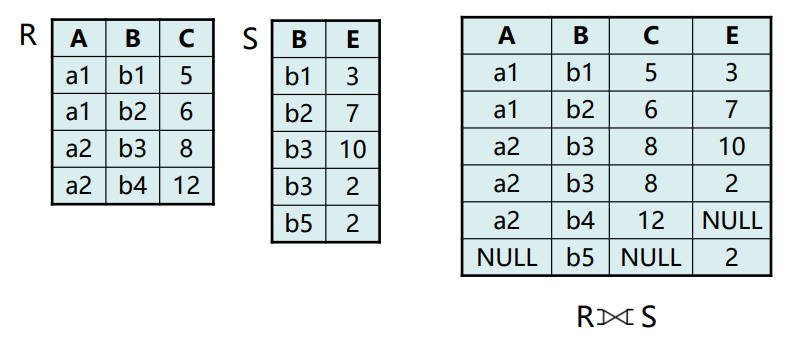
• 全外连接(Full outer join) ⟗
  • 如果把舍弃的元组也保存在结果关系中，而在其他属性上 填空值(Null)，这种连接就叫做外连接（Outer join）

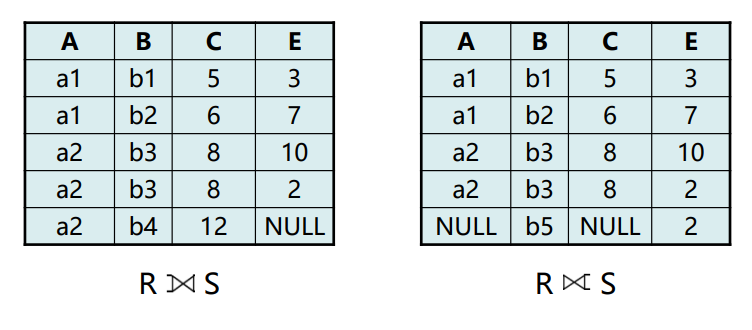
• 左外连接(Left outer join) ⟕
  • 如果只把左边关系R中要舍弃的元组保留就叫做左外连接 (Left Oouter Join或Left Join)
• 右外连接(Right outer join) ⟖
  • 如果只把右边关系S中要舍弃的元组保留就叫做右外连接 (Right outer join或Right join)