树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:
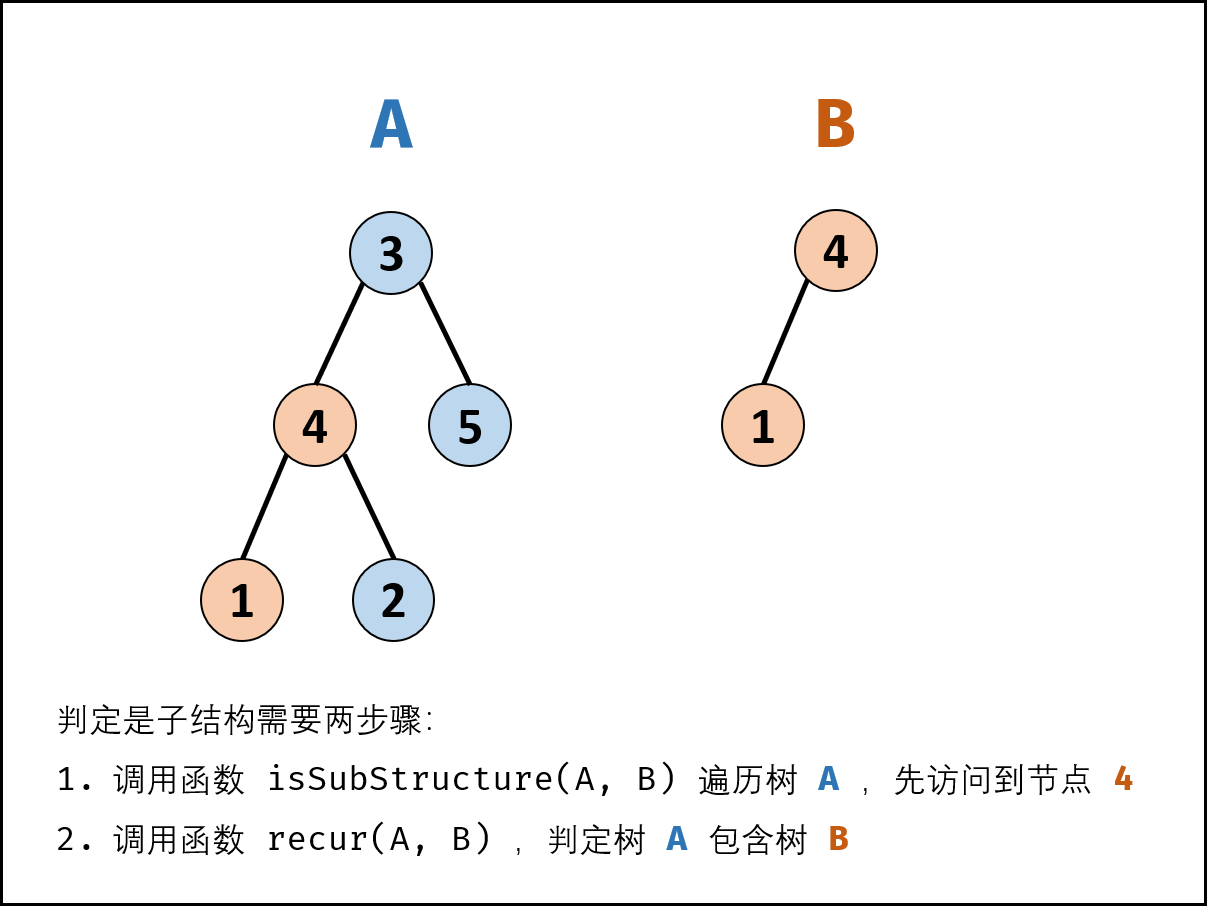
给定的树 A:

     3
    / \
   4   5
  / \
 1   2
给定的树 B：

   4 
  /
 1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

解法：

若树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点。因此，判断树 B 是否是树 A 的子结构，需完成以下两步工作：

1、先序遍历树 A 中的每个节点n ； 对应的函数 isSubStructure(A,B)

2、判断树A种以n为根节点的子树是否包含树B，对应的函数 recur(A,B)   
       

 

 

算法流程：

名词规定：树 A 的根节点记作 节点 A ，树 B 的根节点称为 节点 B 。

recur(A, B) 函数：

终止条件：
　　　　当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true ；
　　　　当节点 A 为空：说明已经越过树 A 叶子节点，即匹配失败，返回 false ；
　　　　当节点 A 和 B 的值不同：说明匹配失败，返回 false ；

返回值：

　　　　判断 A 和 B 的左子节点是否相等，即 recur(A.left, B.left) ；
　　　　判断 A 和 B 的右子节点是否相等，即 recur(A.right, B.right) ；

isSubStructure(A, B) 函数：

特例处理： 当 树 A 为空 或 树 B 为空 时，直接返回 false ；
返回值： 若树 B 是树 A 的子结构，则必满足以下三种情况之一，因此用或 || 连接；
以 节点 A 为根节点的子树 包含树 B ，对应 recur(A, B)；
树 B 是 树 A 左子树 的子结构，对应 isSubStructure(A.left, B)；
树 B 是 树 A 右子树 的子结构，对应 isSubStructure(A.right, B)；

 /*树的子结构*/
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if (A == null || B == null) {
            return false;
        }
        if ((A.val == B.val) && (helper(A.left, B.left) && helper(A.right, B.right))) {
            return true;
        }
        return isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

    private boolean helper(TreeNode A, TreeNode B) {
        if (B == null) {
            return true;
        }
        if (A == null) {
            return false;
        }
        if (A.val == B.val) {
            return helper(A.left, B.left) && helper(A.right, B.right);
        } else {
            return false;
        }
    }