关于珂朵莉树
前言
几个月前学长就讲过珂朵莉树,当时对指针和STL有股莫名的畏惧,咕到现在才入门
定义
用\(STL\)容器维护颜色均摊段
可以理解为不定长度的分块-但一定要有区间推平操作+随机数据
总体来说,是不稳定的优雅的暴力
思想
举个例子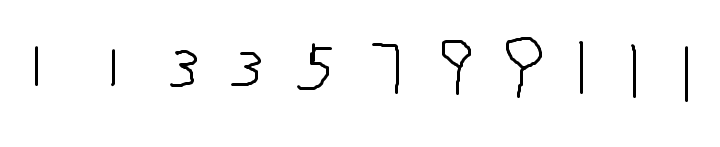 这个序列
这个序列
如何维护每种值所代表的信息?
一种很自然的想法是把相同的值全部放到一起
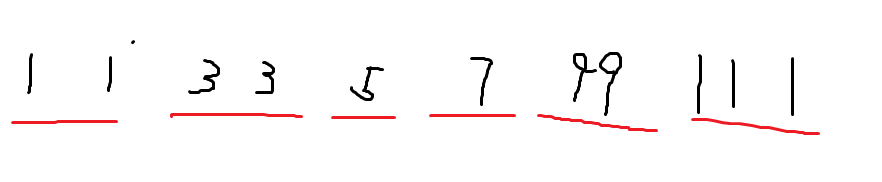
然后维护左右端点,进行直接查询,推出结构体储存
struct Node{
int lz,rz;mutable int val;
Node(int lz,int rz=0,int val=0):lz(lz),rz(rz),val(val){};
inline bool operator<(const Node &x)const{
return lz<x.lz;
}
};
- lz: 左边界下标
- rz: 右边界下标
- val: 当前区间的值
- Node(): 初始化,只需要左值
- 重载<运算符,按照左端点排序
然后就是最重要的\(split\)(分割)函数了
inline auto split(int pos){
auto it=s.lower_bound(Node(pos));
if(it!=s.end()&&it->lz==pos) return it;
it--;
if(it->rz<pos) return s.end();
int l=it->lz,r=it->rz,w=it->val;
s.rease(it);
s.insert(Node(l,pos-1,w));
return s.insert(Node(pos,r,w)).first;
}
先解释一下,这个\(auto\)的全写是
set<Node>::iterator
也就是set的迭代器的意思
逐行解释一下
首先,对于每次推平操作,会有一些Node被合并,也会有一些Node被拆开,\(split\)就是找一个位置pos,把pos对应的Node分割成\([l,pos-1]\)与\([pos,r]\)两个区间,如果pos直接是一个区间的开头或结尾,直接返回区间即可
inline auto split(int pos){//
auto it=s.lower_bound(Node(pos));//查询pos所在区间
if(it!=s.end()&&it->lz==pos) return it;// pos是该区间开头时
it--;//将it往前挪
if(it->rz<pos) return s.end();// pos太大,直接返回s的最后
int l=it->lz,r=it->rz,w=it->val;
s.erase(it);//原来的区间直接删掉
s.insert(Node(l,pos-1,w));//分割成两个小区间
return s.insert(Node(pos,r,w)).first;
}
然后就是合并操作,我喜欢把函数命名为\(gto(get-together)\)
inline void gto(int l,int r,int w){//将区间l~r变成整块值为w的块
auto itr=split(r+1),itl=split(l);//找到左右端点
s.erase(itl,itr);//删除原区间
s.insert(Node(l,r,w));//加入新区间
}
为什么先获取 \(itr\) 再获取 \(itl\) ?
因为如果先分割左边的l,右边的r可能会错位,而先后面再前面就不会错位
基本操作就是这两种,然后就是愉快的暴力拉
例题
1.CF896C Willem, Chtholly and Seniorious
珂朵莉树的起源,就不详细啰嗦了,哪里的题解比我讲得好的多,放个代码叭
/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(x,y) for(auto x:y)
#define wl while
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
#define max(a,b)((a)>(b)?(a):(b))
#define min(a,b)((a)<(b)?(a):(b))
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=2e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
int sed,n,m,vmax;
inline int rnd(){
int res=sed;
sed=(sed*7+13)%1000000007;
return res;
}
struct Node{
int lz,rz;mutable int val;
Node(int lz,int rz=0,int val=0):lz(lz),rz(rz),val(val){};
inline bool operator<(const Node &x)const{
return lz<x.lz;
}
};set<Node>s;
inline auto split(int pos){
auto it=s.lower_bound(Node(pos));
if(it!=s.end()&&it->lz==pos) return it;
it--;
if(it->rz<pos) return s.end();
int l=it->lz,r=it->rz,w=it->val;
s.erase(it);
s.insert(Node(l,pos-1,w));
return s.insert(Node(pos,r,w)).fi;
}
inline void opt1(int l,int r,int w){
auto itr=split(r+1),itl=split(l);
auto it=itl;
for(;it!=itr;it++)
it->val+=w;
}
inline void opt2(int l,int r,int w){
auto itr=split(r+1),itl=split(l);
s.erase(itl,itr);
s.insert(Node(l,r,w));
}
inline void opt3(int l,int r,int x){
auto itr=split(r+1),itl=split(l);
priority_queue<pii,vector<pii>,greater<pii>>q;
for(auto it=itl;it!=itr;it++){
q.push(mk(it->val,(it->rz-it->lz+1)));
}
while(!q.empty()){
int val=q.top().fi,num=q.top().se;
q.pop();
if(num>=x) return cout<<val<<'\n',void();
else x-=num;
}
}
inline int qp(int x,int y,int p,int res=1){
x%=p;
while(y){
if(y&1) res=1LL*res*x%p;
x=1LL*x*x%p;
y>>=1;
}
return res;
}
inline void opt4(int l,int r,int x,int y){
auto itr=split(r+1),itl=split(l);int ans=0;
for(auto it=itl;it!=itr;it++){
int va=qp(it->val,x,y);
ans=(ans+va*(it->rz-it->lz+1)%y)%y;
}
cout<<ans<<'\n';
}
int a[M];
signed main(){
n=read(),m=read(),sed=read(),vmax=read();
rep(i,1,n,1){
a[i]=(rnd()%vmax)+1;
s.insert(Node(i,i,a[i]));
}
rep(i,1,m,1){
int op=(rnd()%4)+1,l=(rnd()%n)+1,r=(rnd()%n)+1,x,y;
if(l>r) swap(l,r);
if(op==3) x=(rnd()%(r-l+1))+1;
else x=(rnd()%vmax)+1;
if(op==4) y=(rnd()%vmax)+1;
// cout<<"op:"<<op<<" l:"<<l<<" r:"<<r<<" x:"<<x<<" y:"<<y<<'\n';
if(op==1) opt1(l,r,x);
if(op==2) opt2(l,r,x);
if(op==3) opt3(l,r,x);
if(op==4) opt4(l,r,x,y);
}
return 0;
}
/*
begin:09:01
end::09:28
*/
2.P4315 月下“毛景树”
看到区间推平,珂朵莉!
#include<bits/stdc++.h>
#define int long long
#define ddq set<Node>::iterator
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
using namespace std;
const int M=2e5+110;
inline int read(){
int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();}
while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();}
return sum*k;
}
struct Node{
int lz,rz;mutable int val;
Node(int lz,int rz=0,int val=0):lz(lz),rz(rz),val(val){};
inline bool operator<(const Node &a)const{
return lz<a.lz;
}
};set<Node>s;
inline ddq split(int pos){
ddq it=s.lower_bound(Node(pos));
if(it->lz==pos&&it!=s.end()) return it;
it--;
if(it->rz<pos) return s.end();
int l=it->lz,r=it->rz,w=it->val;
s.erase(it);
s.insert(Node(l,pos-1,w));
return s.insert(Node(pos,r,w)).fi;
}
inline void gto(int l,int r,int val){
if(l>r) return;
ddq itr=split(r+1),itl=split(l);
s.erase(itl,itr);
s.insert(Node(l,r,val));
}
inline void ad(int l,int r,int val){//暴力遍历之间的每一个区间加值
if(l>r) return;
ddq itr=split(r+1),itl=split(l);
for(ddq it=itl;it!=itr;it++)
it->val+=val;
}
inline int ask(int l,int r){//暴力查找
if(l>r) return -1e18;
int maxx=-1e18;
ddq itr=split(r+1),itl=split(l);
for(ddq it=itl;it!=itr;it++)
maxx=max(maxx,it->val);
return maxx;
}
vector<pair<int,int>> Ed[M];
int a[M],Deep[M],Fa[M],Son[M],Siz[M],Id[M],Top[M],Ti=0;
pair<int,int> edge[M]; // 存储每条边的两个端点
inline void Adde(int u,int v,int w){
Ed[u].push_back(mk(v,w));
Ed[v].push_back(mk(u,w));
}
inline void dfs1(int u,int f){
Fa[u]=f;Deep[u]=Deep[f]+1;
Siz[u]=1;
for(auto i:Ed[u]){
int v=i.fi,w=i.se;
if(v==f) continue;
a[v]=w; // 边权存在子节点上
dfs1(v,u);
Siz[u]+=Siz[v];
if(Siz[Son[u]]<Siz[v])
Son[u]=v;
}
}
inline void dfs2(int u,int topf){
Id[u]=++Ti;Top[u]=topf;
if(!Son[u]) return;
dfs2(Son[u],topf);
for(auto i:Ed[u]){
int v=i.fi;
if(v==Fa[u]||v==Son[u]) continue;
dfs2(v,v);
}
}
inline void ch(int k,int w){//第k条树枝
int u=edge[k].fi,v=edge[k].se;
if(Deep[u]<Deep[v]) swap(u,v);
gto(Id[u],Id[u],w);
}
inline void co(int u,int v,int w){
while(Top[u]!=Top[v]){
if(Deep[Top[u]]<Deep[Top[v]]) swap(u,v);
gto(Id[Top[u]],Id[u],w);
u=Fa[Top[u]];
}
if(Deep[u]>Deep[v]) swap(u,v);
if(u!=v) gto(Id[u]+1,Id[v],w);
}
inline void Add(int u,int v,int w){
while(Top[u]!=Top[v]){
if(Deep[Top[u]]<Deep[Top[v]]) swap(u,v);
ad(Id[Top[u]],Id[u],w);
u=Fa[Top[u]];
}
if(Deep[u]>Deep[v]) swap(u,v);
if(u!=v) ad(Id[u]+1,Id[v],w);
}
inline int Max(int u,int v){
int maxx=-1e18;
while(Top[u]!=Top[v]){
if(Deep[Top[u]]<Deep[Top[v]]) swap(u,v);
maxx=max(maxx,ask(Id[Top[u]],Id[u]));
u=Fa[Top[u]];
}
if(Deep[u]>Deep[v]) swap(u,v);
if(u!=v) maxx=max(maxx,ask(Id[u]+1,Id[v]));
return maxx;
}
signed main(){
int n=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
edge[i]=mk(u,v); // 存储边的两个端点
Adde(u,v,w);
}
dfs1(1,0);dfs2(1,1);
for(int i=1;i<=n;i++) s.insert(Node(Id[i],Id[i],a[i]));//新序列的珂朵莉树,对Id[i]建
while(1){
string cs;cin>>cs;
if(cs=="Stop") break;
if(cs=="Change"){
int k=read(),w=read();
ch(k,w);
}
else if(cs=="Cover"){
int u=read(),v=read(),w=read();
co(u,v,w);
}
else if(cs=="Add"){
int u=read(),v=read(),w=read();
Add(u,v,w);
}
else if(cs=="Max"){
int u=read(),v=read();
printf("%lld\n",Max(u,v));
}
}
return 0;
}
- P5350 序列
想一想暴力取出的魅力
#include<bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f
#define ddq set<Node>::iterator
using namespace std;
const int M=2e5+110,Mod=1e9+7;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));
}
struct Node{
int lz,rz;mutable int val;
Node(int lz,int rz=0,int val=0):lz(lz),rz(rz),val(val){};
inline bool operator<(const Node &a)const{
return lz<a.lz;
}
};set<Node>s;
inline ddq split(int pos){
ddq it=s.lower_bound(Node(pos));
if(it!=s.end()&&it->lz==pos) return it;
it--;
if(it->rz<pos) return s.end();
int l=it->lz,r=it->rz,val=it->val;
s.erase(it);
s.insert(Node(l,pos-1,val));
return s.insert(Node(pos,r,val)).first;
}
inline void gto(int l,int r,int val){
ddq itr=split(r+1),itl=split(l);
s.erase(itl,itr);
s.insert(Node(l,r,val%Mod));
}
inline void ad(int l,int r,int val){
ddq itr=split(r+1),itl=split(l);
for(ddq it=itl;it!=itr;it++)
it->val+=val,it->val%=Mod;
}
inline void ask(int l,int r){
ddq itr=split(r+1),itl=split(l);int res=0;
for(ddq it=itl;it!=itr;it++)
res+=(((it->rz)-(it->lz)+1)*(it->val));
wr(res%Mod);putchar('\n');
}
int n,m,tot=0,va[M],ls[M],rs[M];
inline void cop(int l1,int r1,int l2,int r2){
ddq itr=split(r1+1),itl=split(l1);
for(ddq it=itl;it!=itr;it++)
ls[++tot]=l2+it->lz-l1,rs[tot]=l2+it->rz-l1,va[tot]=it->val;
for(int i=1;i<=tot;++i){
gto(ls[i],rs[i],va[i]);
}tot=0;
}
inline void ex(int l1,int r1,int l2,int r2){
if(l2>l1) swap(l1,l2),swap(r1,r2);
cop(l1,r1,n+1,n+r1-l1+1);
cop(l2,r2,l1,r1);
cop(n+1,n+r1-l1+1,l2,r2);
}
vector<Node>g;
inline void fan(int l,int r){
ddq itr=split(r+1),itl=split(l);
int aa=r;g.clear();
for(ddq it=itl;it!=itr;it++){
int l=it->lz,r=it->rz,vl=it->val;
g.push_back(Node(l,r,vl));
}
s.erase(itl,itr);
for(int i=0;i<(int)g.size();i++){
s.insert(Node(aa-(g[i].rz-g[i].lz),aa,g[i].val));
aa-=(g[i].rz-g[i].lz+1);
}
}
inline void la(){
ddq itr=split(n+1),itl=split(1);
for(ddq it=itl;it!=itr;it++)
for(int i=it->lz;i<=it->rz;i++)
wr(it->val),putchar(' ');
putchar('\n');
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) s.insert(Node(i,i,read()));
while(m--){
int opt=read();
if(opt==1){
int l=read(),r=read();
ask(l,r);
}else if(opt==2){
int l=read(),r=read(),val=read();
gto(l,r,val);
}else if(opt==3){
int l=read(),r=read(),val=read();
ad(l,r,val);
}else if(opt==4){
int l1=read(),r1=read(),l2=read(),r2=read();
cop(l1,r1,l2,r2);
}else if(opt==5){
int l1=read(),r1=read(),l2=read(),r2=read();
ex(l1,r1,l2,r2);
}else if(opt==6){
int l=read(),r=read();
fan(l,r);
}
}
la();
return 0;
}
- P5251 [LnOI2019] 第二代图灵机
线段树,珂朵莉一起维护
/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(x,y) for(auto x:y)
#define wl while
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=2e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
struct Node{
int lz,rz;mutable int col;
Node(int lz,int rz=0,int val=0):lz(lz),rz(rz),col(val){};
inline bool operator <(const Node &x)const{
return lz<x.lz;
}
};set<Node>s;
inline auto split(int pos){//
auto it=s.lower_bound(Node(pos));//查询pos所在区间
if(it!=s.end()&&it->lz==pos) return it;//pos是该区间开头时
it--;//将it往前挪
if(it->rz<pos) return s.end();//psos太大,直接返回s的最后
int l=it->lz,r=it->rz,w=it->col;
s.erase(it);//原来的区间直接删掉
s.insert(Node(l,pos-1,w));//分割成两个小区间
return s.insert(Node(pos,r,w)).first;
}
int n,m,c,a[M],b[M],sum[M<<2],mx[M<<2],mi[M<<2];
inline void build(int id,int l,int r){
if(l==r)
return sum[id]=mx[id]=mi[id]=a[l],void();
int Mid=(l+r)>>1;
build(ls,l,Mid);build(rs,Mid+1,r);
sum[id]=sum[ls]+sum[rs];
mx[id]=max(mx[ls],mx[rs]);
mi[id]=min(mi[ls],mi[rs]);
}
inline int ask_Sum(int id,int l,int r,int L,int R){
if(l>=L&&r<=R) return sum[id];
int Mid=(l+r)>>1,res=0;
if(Mid>=L) res+=ask_Sum(ls,l,Mid,L,R);
if(Mid<R) res+=ask_Sum(rs,Mid+1,r,L,R);
return res;
}
inline int ask_Max(int id,int l,int r,int L,int R){
if(l>=L&&r<=R) return mx[id];
int Mid=(l+r)>>1,res=-INF;
if(Mid>=L) res=max(res,ask_Max(ls,l,Mid,L,R));
if(Mid<R) res=max(res,ask_Max(rs,Mid+1,r,L,R));
return res;
}
inline int ask_Min(int id,int l,int r,int L,int R){
if(l>=L&&r<=R) return mi[id];
int Mid=(l+r)>>1,res=INF;
if(Mid>=L) res=min(res,ask_Min(ls,l,Mid,L,R));
if(Mid<R) res=min(res,ask_Min(rs,Mid+1,r,L,R));
return res;
}
inline void upt(int id,int l,int r,int pos,int val){
if(l==r) return sum[id]=mx[id]=mi[id]=val,void();
int Mid=(l+r)>>1;
if(Mid>=pos) upt(ls,l,Mid,pos,val);
else upt(rs,Mid+1,r,pos,val);
sum[id]=sum[ls]+sum[rs];
mx[id]=max(mx[ls],mx[rs]);
mi[id]=min(mi[ls],mi[rs]);
}
inline void opt1(int pos,int val){
return upt(1,1,n,pos,val),void();
}
inline void opt2(int l,int r,int y){
auto itr=split(r+1),itl=split(l);
s.erase(itl,itr);
return s.insert(Node(l,r,y)),void();
}
int cnt[105];
inline void opt3(int L,int R){
int ans=INF,sum=0;
rep(i,1,c,1) cnt[i]=0;
if(c==1){
return cout<<ask_Min(1,1,n,L,R)<<'\n',void();
}
auto itr=split(R+1),itl=split(L);
for(auto l=itl,r=itl;r!=itr;r++){
if(!cnt[r->col])sum++;
cnt[r->col]++;
while(sum==c&&cnt[l->col]>1){
cnt[l->col]--;
if(cnt[l->col]==0) sum--;
l++;
}
if(sum==c)ans=min(ans,ask_Sum(1,1,n,l->rz,r->lz));
}
wr(ans==INF?-1:ans),pr(10);
}
inline void opt4(int L,int R){
int ans=ask_Max(1,1,n,L,R),sum=0;
rep(i,1,c,1) cnt[i]=0;
auto itr=split(R+1),itl=split(L);
for(auto l=itl,r=itl;r!=itr;r++){
if(r->rz-r->lz+1>1)sum++;
cnt[r->col]++;
while((sum-((l->rz-l->lz+1)>1)-((r->rz-r->lz+1)>1)>0)||cnt[r->col]>1){
cnt[l->col]--;
sum-=((l->rz-l->lz+1)>1);
l++;
}
// cout<<"l:"<<l->rz<<" r:"<<r->lz<<" ans:"<<ans<<'\n';
ans=max(ans,ask_Sum(1,1,n,l->rz,r->lz));
}
wr(ans),pr(10);
}
signed main(){
n=read();m=read();c=read();
rep(i,1,n,1) a[i]=read();
rep(i,1,n,1) b[i]=read(),s.insert(Node(i,i,b[i]));
build(1,1,n);
rep(i,1,m,1){
int opt=read();
if(opt==1){
int x=read(),y=read();
opt1(x,y);
}
if(opt==2){
int l=read(),r=read(),y=read();
opt2(l,r,y);
}
if(opt==3){
int l=read(),r=read();
opt3(l,r);
}
if(opt==4){
int l=read(),r=read();
opt4(l,r);
}
}
return 0;
}
/*
*/
- P2391 白雪皑皑
版子
#include<bits/stdc++.h>
#define ddq set<Node>::iterator
#define int long long
#define fi first
#define se second
using namespace std;
const int M=2e5+110;
inline int read(){
int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}
struct Node{
int lz,rz;mutable int val;
Node(int lz,int rz=0,int val=0):lz(lz),rz(rz),val(val){};
inline bool operator<(const Node &a)const{
return lz<a.lz;
}
};set<Node>s;
inline auto split(int pos){//
auto it=s.lower_bound(Node(pos));//查询pos所在区间
if(it!=s.end()&&it->lz==pos) return it;//pos是该区间开头时
it--;//将it往前挪
if(it->rz<pos) return s.end();//psos太大,直接返回s的最后
int l=it->lz,r=it->rz,w=it->val;
s.erase(it);//原来的区间直接删掉
s.insert(Node(l,pos-1,w));//分割成两个小区间
return s.insert(Node(pos,r,w)).first;
}
inline void gto(int l,int r,int w){//将区间l~r变成整块值为w的块
auto itr=split(r+1),itl=split(l);//找到左右端点
s.erase(itl,itr);//删除原区间
s.insert(Node(l,r,w));//加入新区间
}
signed main(){
int n=read(),m=read(),p=read(),q=read();
s.insert(Node(1,n,0));
for(int i=(n<m)?m-n:1;i<=m;i++){
int l=(i*p+q)%n+1,r=(i*q+p)%n+1;
if(l>r) swap(l,r);
gto(l,r,i);
}
ddq itr=split(n+1),itl=split(1);
for(ddq it=itl;it!=itr;it++){
int sum=it->rz-it->lz+1,va=it->val;
for(int i=1;i<=sum;i++) printf("%lld\n",va);
}
return 0;
}



 我永远喜欢珂朵莉
我永远喜欢珂朵莉

 浙公网安备 33010602011771号
浙公网安备 33010602011771号