如何打麻将

初始思想：

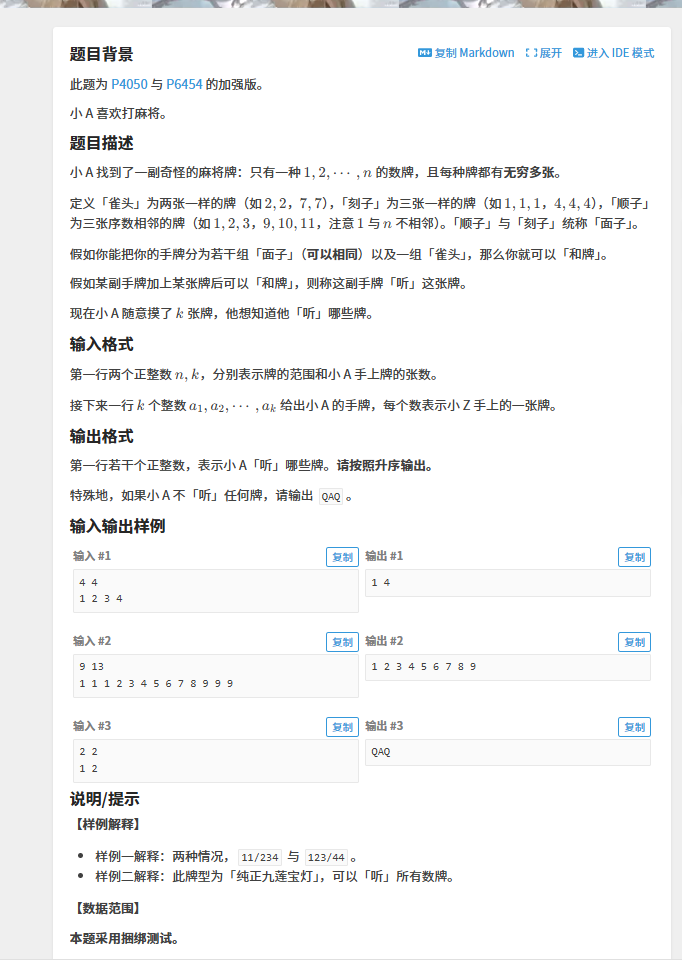
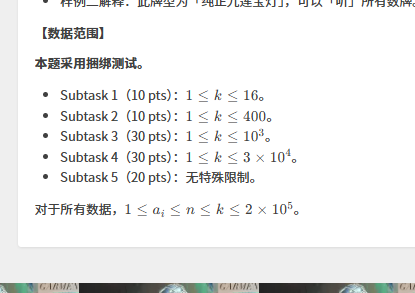
定义\(f[i][j][k][0/1][0/1]\)

• 表示第i种牌

• 有j个（i-2）开始的顺子

• 有k个（i-1）开始的顺子

• 有无雀头，是否添加过牌

对转移建图，从终点回溯遍历

当遇见\(f_{i,?,?,?,1}->f_{i-1,?,?,?,0}的边，就可以说明为添加了i\)

由于从终点状态回溯，不会遇见不合理状态，且多组雀头可以用判否？

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=1e6+110;
inline int read(){
	int sum=0,k=1;char c=getchar();
	while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
	}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
	}return sum*k;
}
int n,kk,a[M],ch,cnt,ans[M];
bool vis[M],f[M][5][5][3];//f判断该状态 是否成立 
vector<int>Ed[M],G[M];
inline void dfs(int u){
	for(auto v:G[u]) vis[v]=true;
	for(auto v:Ed[u]) dfs(v);
}
inline int gi(int i,int j,int k,int p){
	return i*18+j*6+k*2+p;
	//建边的id 
}
signed main(){
	n=read(),kk=read();
	for(int i=1;i<=kk;i++) ch=read(),a[ch]++;
	f[0][0][0][0]=true;
	for(int i=0;i<n;i++){
		for(int j=0;j<=2;j++)//确定是否可以转移 
			for(int k=0;k<=2;k++)
				for(int p=false;p<=1;p++){
					if(!f[i][j][k][p]) continue;
					if(a[i+1]>=j+k) f[i+1][k][(a[i+1]-j-k)%3][p]=true;
					if(p==false)
						if(a[i+1]>=j+k+2)//雀头 
							f[i+1][k][(a[i+1]-j-k-2)%3][1]=true;
				}
		for(int j=0;j<=2;j++)
			for(int k=0;k<=2;k++)
				for(int p=false;p<=1;p++){
					int id=gi(i,j,k,p);
					if(a[i+1]>=j+k) Ed[gi(i+1,k,(a[i+1]-j-k)%3,p)].push_back(id);
					if(p==false)//此时没有雀头 
						if(a[i+1]>=j+k+2)
							Ed[gi(i+1,k,(a[i+1]-j-k-2)%3,1)].push_back(id);
				} 
		a[i+1]++;//加牌 
		for(int j=0;j<=2;j++)
			for(int k=0;k<=2;k++)
				for(int p=false;p<=1;p++){
					if(!f[i][j][k][p]) continue;
					if(a[i+1]>=j+k) G[gi(i+1,k,(a[i+1]-j-k)%3,p)].push_back(i+1);
					if(p==false)
						if(a[i+1]>=j+k+2)
							G[gi(i+1,k,(a[i+1]-j-k-2)%3,1)].push_back(i+1);
				}
	}
	dfs(gi(n,0,0,1));
	for(int i=1;i<=n;i++)
		if(vis[i]) ans[++cnt]=i;
	if(cnt==0) printf("QAQ\n");
	for(int i=1;i<=cnt;i++) cout<<ans[i]<<' ';
	return 0;
}

new写法

定义\(f[i][j][k][p]\)表示

-第\(i\)种牌

• 有\(j\)个\((i-2)\)开始的顺子

• 有\(k\)个\((i-1)\)开始的顺子

• 有雀头时\(p=1\),无雀头时\(p=0\)

• 转移方程:

• \(f_{i,j,k,p}->f_{i+1,k,a[i+1]-j-k,p}\)

• $f_{i,j,k,0} -> f_{i+1,k,a[i+1]-j-k-2,1} $

• 三个顺子直接用刻子秒掉

• 所以转移要mod3

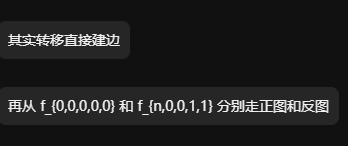
• 对转移的合法状态建图

• 每次尝试加第一张\(i+1\)的牌

• 再对加牌情况建第二个图

• 从终点状态往回遍历

• 如果是合法状态,加牌也会是合法的

• 数组枚举