dp笔记_四边形不等式的判定

凸性

• 几何体中任意两点的中点仍在几何体中，则可称该几何体为凸的。

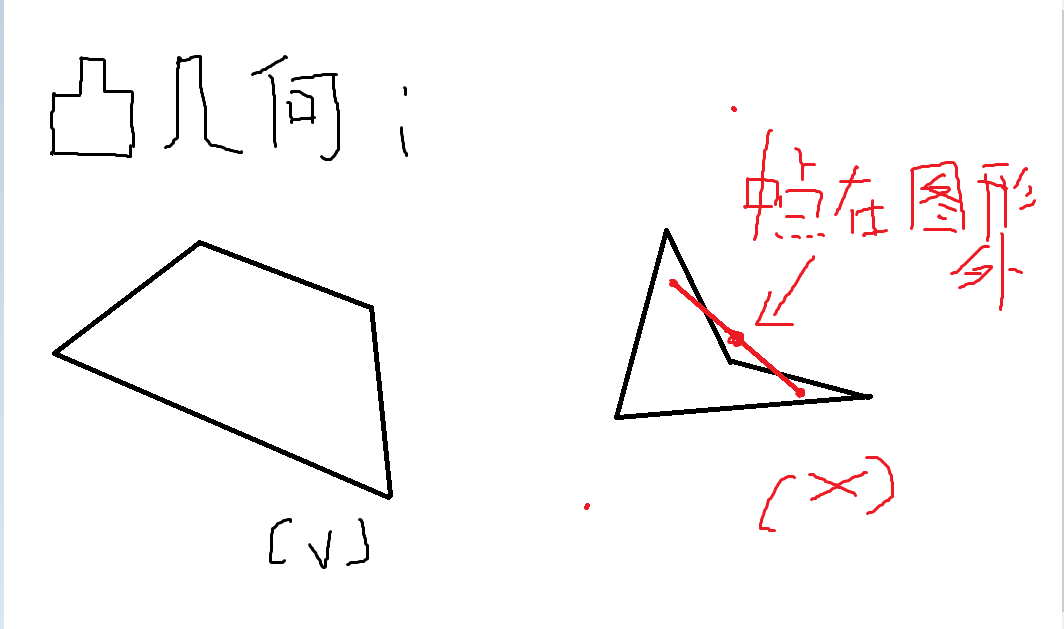
• 如果称一个一元函数是凸的，则几何体 \((x,y)|f(x)<=y\) 为凸的

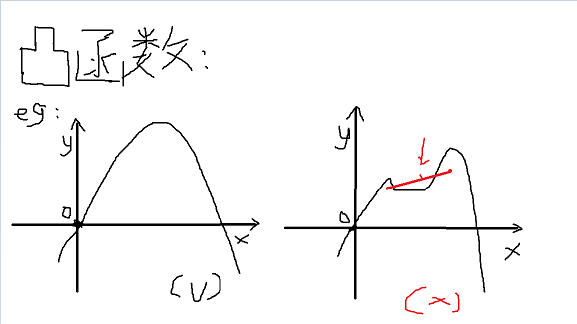
• 该函数的导数单调不降

• \(f(x_1)+f(x_2)>=2f( \frac{x_1+x_2}{2} )\)

• \(f\)的边际效应递增

边际效应

eg: 跑一次800m需要3min+10s，而跑一次400m仅需1min+20s，越跑越累

也就是代价会随着参数上涨上升趋势不降

刻画二维的边际效应递增：

• 对于任意区间\([a,c] [b,c]\)其中\(a<=b<=c\)

• \(f(a,c+1)-f(a,c)>=f(b,c+1)-f(b,c)\)

• 给长区间加一个东西，比给短区间加一个东西代价更大

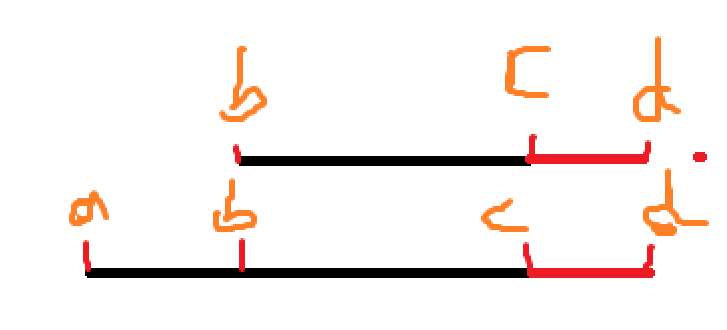
比如区间逆序对，同样有b ~ c的区间，但下方因为长一截，所以加上同一段c ~ d的逆序对变化量大于等于上方

所以可以通过上图得到：

• $f(a,d)-f(a,c)>=f(b,d)-f(b,c) $

• \(其中a<=b<=c<=d\)

• 移项：\(f(a,d)+f(b,c)>=f(a,c)+f(b,d)\)

• 这就是所谓四边形不等式

wqs二分

• 恰好选k个元素

• 将序列分为k段的最小代价

• 优化掉dp中记录选取个数那一维

思想

• dp时不限制个数

• 选择时为多选的选择加上额外代价

• 选择时为少选的选择给予额外奖励

• 如果多少严格单调，二分（代价/奖励）

例题1： P2619 [国家集训队] Tree I

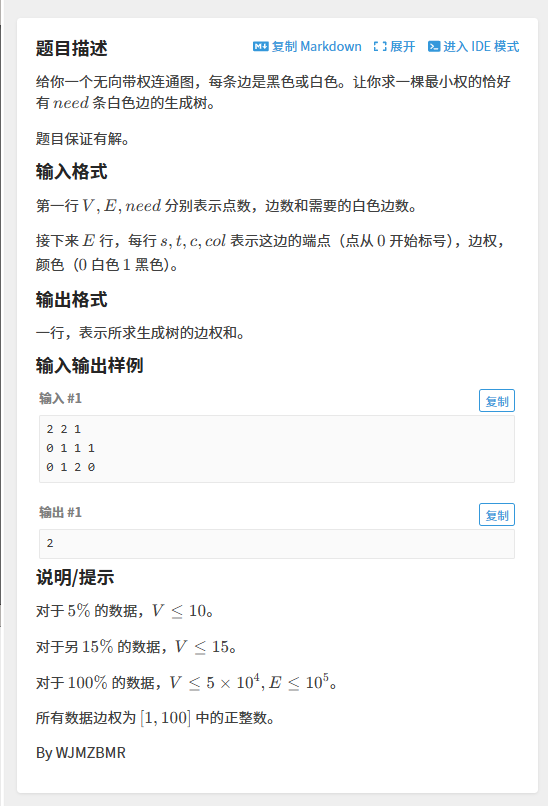
要选择k条白边的生成树，又看到边权在1~100

二分加权边界，跑最小生成树即可，答案要减去加权

例题2： 咕咕咕

斜率优化

观察形如此样的dp方程：

• \(f_i=A_i+max(f_j+B_j)+C_iC_j\)

• 即：与i，j都有关的只有乘积项

• \(y=kx+b\) 秒了

• 截距b： \(f_j+B_j\)

• 斜率k： \(C_j\),横坐标x： \(C_i\)

由于我最近学了李超线段树，就介绍李超树维护吧

• [数据删除]

快去做题