关于网络流

在我的理解里，网络流就是一张有向图，图上是管道，注入的水太多，管道会爆

详细解释：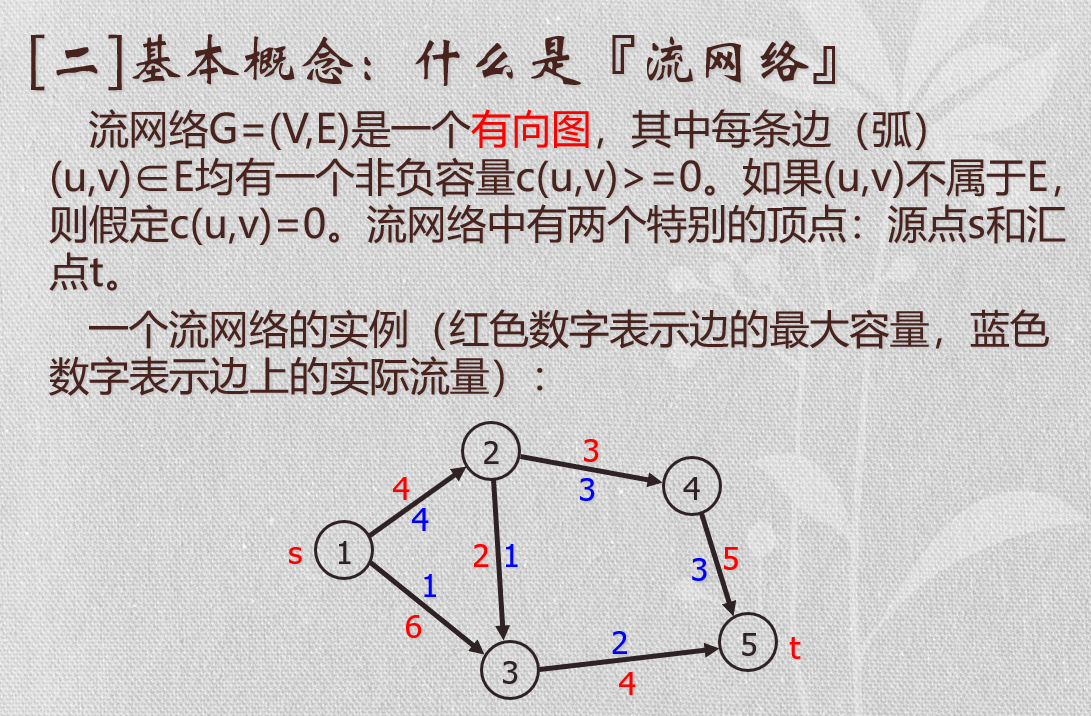

就是 有向图 管道输水，要从 水厂 送到 你家 ，你 买了多少水，水厂 就从各条管道给你送 多少 水~

这个水是专门供给你家的,所以不会只留在半路上

水厂是 源点\(s\) ,你家是 汇点\(t\) ,管道 \(u->v\) 的容量限制称为 \(c(u,v)\) ,所有限制不可能 小于0

由此可提出网络流的基本定理:

定义每条管道 \(u->v\) 实际运输水量为 \(f(u,v)\) ,显然可得 \(f(u,v)<=c(u,v)\)

整个网络的总流就是源点\(s\)流向儿子们的总和,也是汇点\(t\)的父亲流向\(t\)的流量总和

公式为\(|f|= \sum{f(s,v)}= \sum{f(u,t)}\)

还有一个很简单的定义:

• 每一条输水路径叫做 可行流

• 可行流中流量最大的叫做 最大流 (可能不止一条)

残留网络+增广路径

很简单的定义 : 定义残留容量为\(c_f(u,v)\)则:

\(c_f(u,v)=c(u,v)-f(u,v)\),就是(u->v)管道的剩余容量

那么所有的残留容量就可以构成该图的 残留网络

有了残留网络就可以了解 增广路径 了

定义太长,挂个图吧:

很明显,在增广路径中,不会存在流量为0的路线了
知道了增广路径,就对接下来的最大流有帮助了)

割

割(CUT)相当于将网络流分成了两个部分: \(S\) 和 \(T\) ,其中 原点\(s\in S\),汇点\(t /in T\).
记作 \(CUT(S,T)\)
如果有一条边是连接了两个部分,那么称改边为一条割\(CUT(S,T)\)的割边

• 从 S->T 叫正向割边
• 从 T->S 叫反向割边

割\(CUT(S,T)\) 的所有正向割边和为其 容量

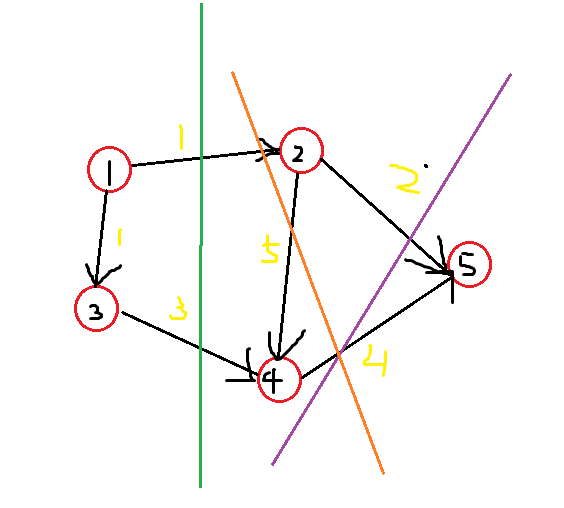
绿线,紫线,橙线都是割

网络流的三大霸主

• 最大流

1. 定理:
   若当前可行流 \(f\) 是最大流,那么不会存在关于 \(f\)的增广路径
   显然啊,增广路径是经过该边至汇点的新路线,有新水,原来的就不会是最多的了.
2. 定理:
   当且仅当当前流 \(f\) 的残留网络中不存在增广路时,\(f\)的流量\(|f|\)达到最大.
   找不出新路线,你就是老大)
3. dinic求最大流
   dinic 比起 EK 算法最改进的是实现了多路增广
   三个步骤:

• bfs分层
• dfs增广
• 重复执行,直到再无增广路

分层:

由原点 S 为起点,到S距离相等的点是一层

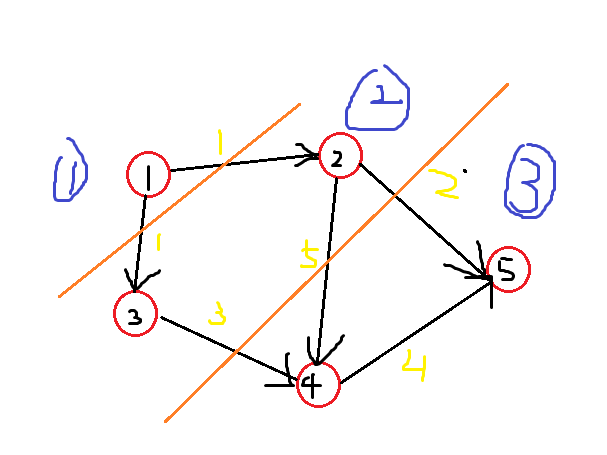
上图分了三层,分层作用?
当U->V的路径满足 \(dep[v]=dep[u]+1\)
该路径为一条最短增广路径,可以避免

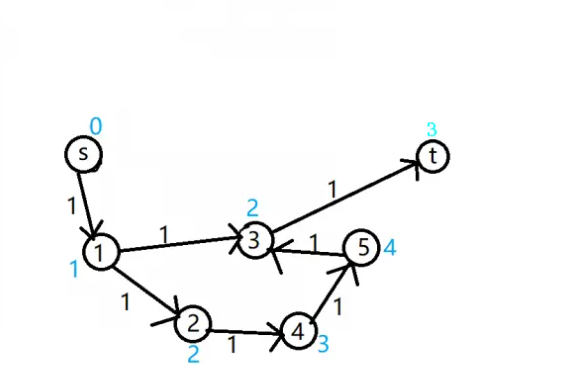
有了分层，我们就不会选s->1->2->4->5->3->t了
/

#include<bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f
using namespace std;
const int M=2e5+110;
inline int read(){
	int sum=0,k=1;char c=getchar();
	while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
	}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
	}return sum*k;
}
struct Line_Node{
	int Next,To,Val;
}Ed[M];
int Head[M],Tot=1;
inline void Adde(int u,int v,int w){
	Ed[++Tot]={Head[u],v,w};
	Head[u]=Tot;
}
int Deep[M];bool vis[M];
int n,m,s,t,cur[M];
inline bool dfs1(int s,int t){//分层,判断是否有增广路
	for(int i=0;i<=n;i++) Deep[i]=INF,cur[i]=Head[i],vis[i]=false;
	//Deep为深度
	//cur拷贝节点的最后一条边优化用
	//vis表示是否已经建立深度关系
	Deep[s]=0;queue<int>q;//初始化
	q.push(s);
	while(!q.empty()){
		int u=q.front();q.pop();
		vis[u]=false;//bfs,不重复访问
		for(int i=Head[u];i;i=Ed[i].Next){
			int v=Ed[i].To,w=Ed[i].Val;
			if(Deep[v]>Deep[u]+1&&w!=false){
				//流量为0不取
				Deep[v]=Deep[u]+1;
				if(!vis[v]) q.push(v),vis[v]=true;
			}
		}
	}
	//到不了终点
	if(Deep[t]==INF) return false;
	else return true;
}
inline int dfs2(int u,int mi,int s,int t,int mm=0){//dfs寻找增广路过程
	if(u==t) return mi;//到达终点
	for(int i=cur[u];i;i=Ed[i].Next){
		cur[u]=i;//不会重复走
		int v=Ed[i].To,w=Ed[i].Val;
		if(Deep[v]==Deep[u]+1&&w!=false){
			//分层图!
			mm=dfs2(v,min(mi,w),s,t);
			if(mm!=false){
				Ed[i].Val-=mm;//正图
				Ed[i^1].Val+=mm;//反图
				return mm;
			}
		}
	}
	return 0;
}
inline int Dinic(int s,int t){
	int ans=0,res=0;
	while(dfs1(s,t))//初始化最大值
		while(res=dfs2(s,INF,s,t))
			ans+=res;		
	return ans;
}
signed main(){
	scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		Adde(u,v,w),Adde(v,u,0);
	}printf("%lld\n",Dinic(s,t));
	return 0;
}
/*
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 30
*/

就是在有路的情况下不停寻找增广路,累加答案即可

• 当前弧优化:
  在dfs时,不访问其已经访问过了的边,将其打 废