树、二叉树、查找算法的总结

一、思维导图

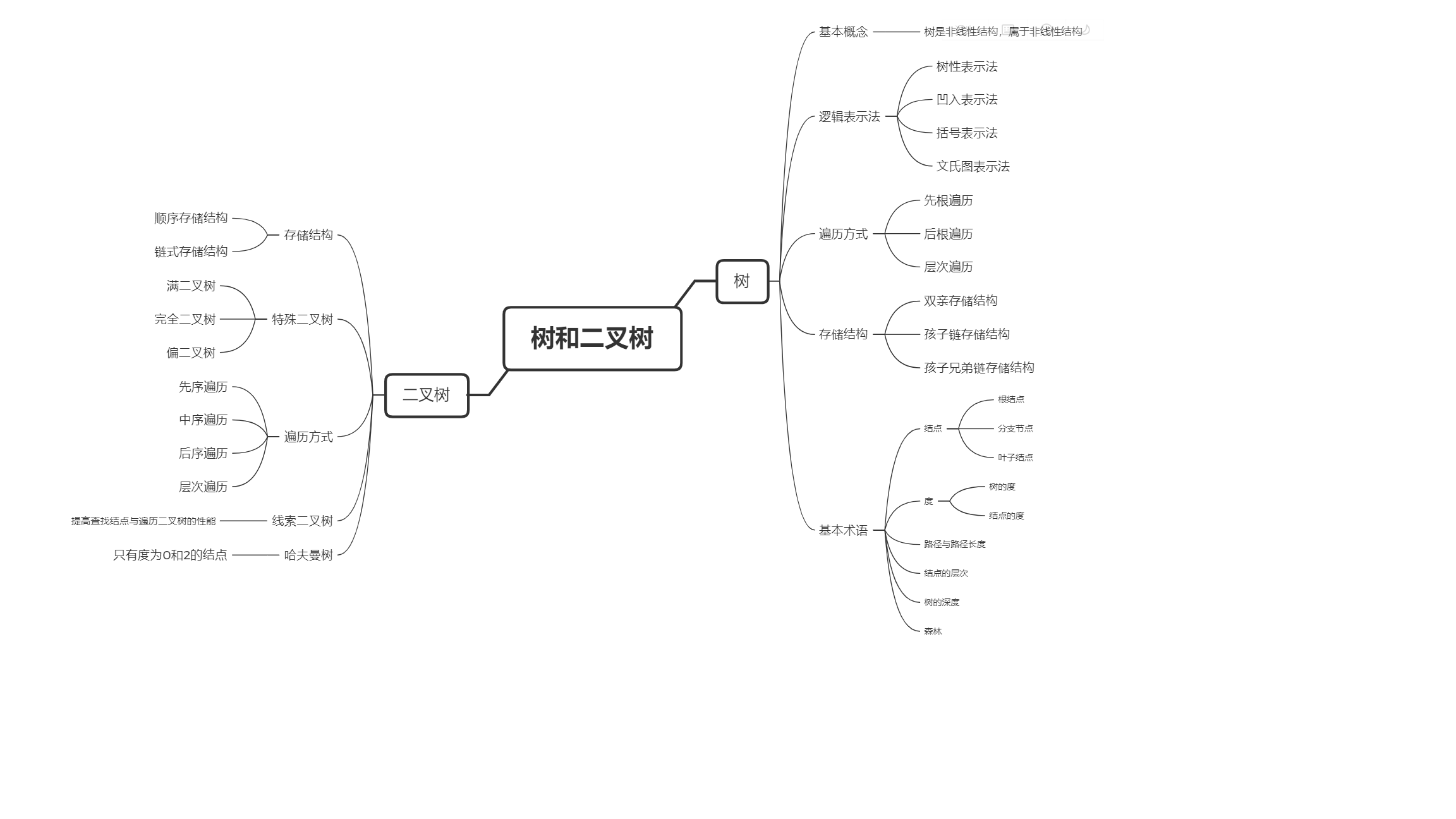
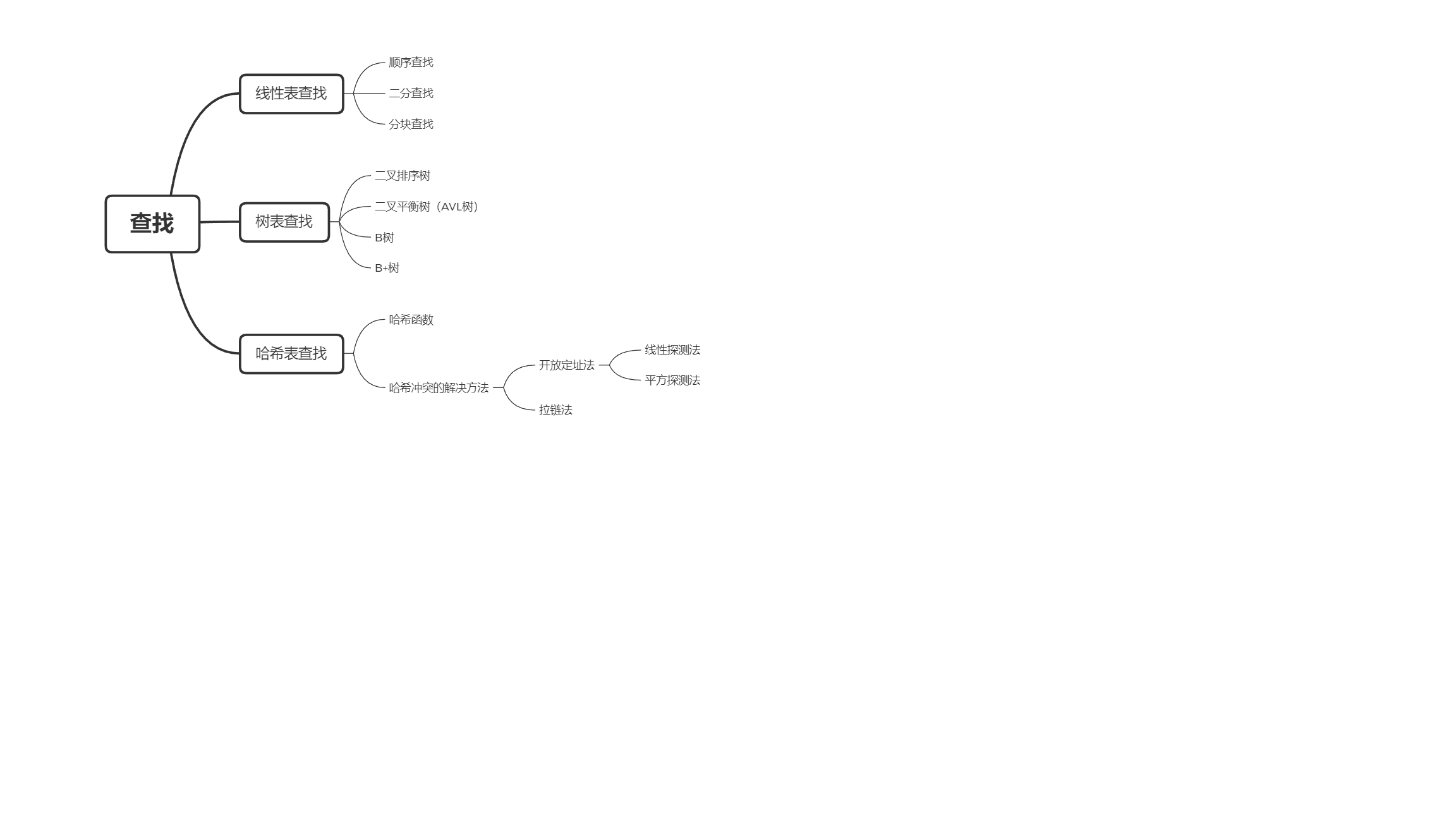
二、重要概念的笔记

1.树的定义

树是由n(n>=0)个结点构成的有限集合。

2.树的性质

1）树中的结点数等于所有结点的度数加1。

2）度为m的树中第i层上至多有m^(i-1)个结点，这里应有i>=1。

3）高度为h的m次树之多有（m^h-1）/（m-1）个结点。

4）具有n个结点的m次数的最小高度为[logm(n(m-1)+1)].

3.树的存储

1）双亲存储结构：求双亲节点更方便。
2）孩子存储结构：求孩子节点更方便。
3）孩子兄弟存储结构：是树与二叉树之间的转换更加方便。

4.二叉树的性质

1）在二叉树的第i层上至多有2^(i-1)个结点。

2）深度为h的二叉树上至多含有2^(h-1)个结点(h>=1)。

3）对任何一棵二叉树，若它含有n0个叶子节点、n2个度为2的结点，则必存在关系式：n0 = n2+1。

4）若含有n个节点的完全二叉树从上到下且从左到右进行1至n的编号，则对完全二叉树中任意一个编号为i的结点。

5）具有n个(n>0)结点的完全二叉树的高度为h=[log2n]+1或h=[log2(n+1)]。

5.线索二叉树

概念：在二叉树中通过添加分量并且使用原有的空指针存储遍历顺序的过程为二叉树的线索化，相应的二叉树称为线索二叉树。

意义：提高查找结点与遍历二叉树的性能。

6.线性表查找

顺序查找：1）算法简单

​ 2）对表的结构无任何要求

​ 3）查找效率低（平均查找长度为（n+1）/2）

二分查找：相对于顺序查找效率更高。

7.树表查找

二叉排序树：平均查找时间为O(log2n)。

AVL树：子树之间高度差的绝对值不超过1。

8. 哈希冲突的解决方法：

1）开放定址法:
线性探测法： 冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。
二次探查法： 冲突发生时，在表的左右进行跳跃式探测，比较灵活。

2）拉链法：将所有关键字为同义词的结点链接在同一个单链表中。
优点：
拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短。
由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况。
在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。

三、疑难问题及解决方案

用开放定址法解决哈希冲突

先将所有关键字分别除以哈希表长度，得出所有关键字对应的余数。然后按照关键字的顺序一个个填入表中，如果产生冲突，则按照选用的是线性探测法还是二次探查法。

线性探测法：按顺序找表中冲突位置的下一个空位，或遍历全表。

二次探查法：找冲突位置的左右两边，先从左边找起一个个寻找。