第一次接触到哈希的这种用法

前置知识，可以去这篇文章里看看
卡特兰数

先考虑没有计划的情况，显然就是一个括号匹配，直接套卡特兰数\(H_m=\frac{(2m)!}{m!(m+1)!}\)
那么如果有一个计划呢？如下图

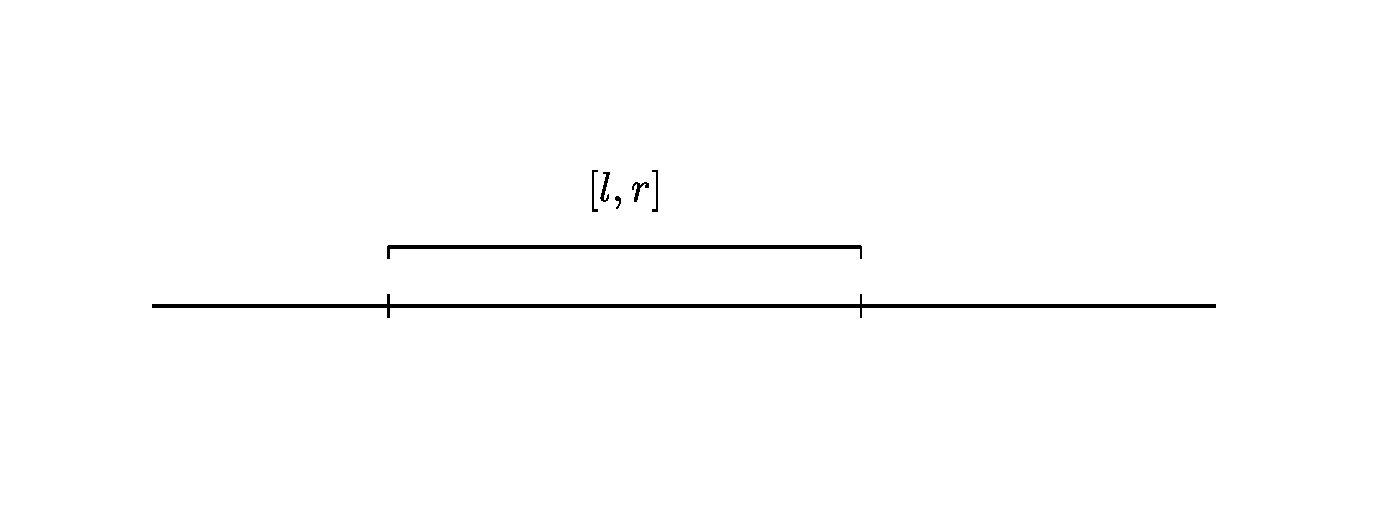
因为\([l,r]\)内部要匹配，总体也要匹配，所以除去该区间的部分也应该匹配，将两个部分分别计算相乘即可
那么当我们有两个计划呢？

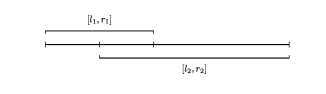
会有重叠部分，我们记\([l_1,l_2),[l_2,r_1],(r_1,r_2]\)喝酒和吃药的次数分别为\(x_1,y_1,x_2,y_2,x_3,y_3\)
则有
\(\left\{\begin{matrix} x_1+x_2=y_1+y_2\\ x_2+x_3=y_2+y_3\\ x_1\ge y_1\\ x_2\ge y_2 \end{matrix}\right.\)
显然只有一种解
\(\left\{\begin{matrix} x_1=y_1\\ x_2=y_2\\ x_3=y_3 \end{matrix}\right.\)
也就是说，对于被不同计划组包含的区间要分别匹配
但总共有\(2^k\)种计划组合，存不下啊……
诶，虽然你总共有\(2^k\)种，但只会最多出现\(n\)种不同的情况
于是我们想到哈希：对于每一个计划，给予一个随机值，在它的开始位置和结束位置将这个值异或上去，最后前缀疑惑和即可得到每个区间的不同哈希值，哈希值相同的归为一类一起处理，最后将每一类的答案相乘即可
但还有几点需要注意：
1.这题的\(n\)是总天数，而公式中的\(m\)是两者分别的数量，代入时应当除以\(2\)
2.若某类的天数为奇数，显然两者无法相等，需要特判输出\(0\)
应该差不多了，加油