in front :
学习的前置条件:熟悉掌握并理解二叉树与递归
线段树:
线段树(Segment Tree)是一种基于分治思想的二叉树结构,用于解决一些区间上的信息统计。(易于维护一些满足区间可加、可减的信息)
add:分治思想:将一个难以直接解决的大问题,分割成一些规模较小的相同或相似的问题,以便各个击破,分而治之。
另外与线段树相似的树状数组基于二进制划分与倍增思想 、分块的基本思想是适当的划分。
这篇文章主要是讲解一些区间问题并使用线段树解决
线段树的具体意义:
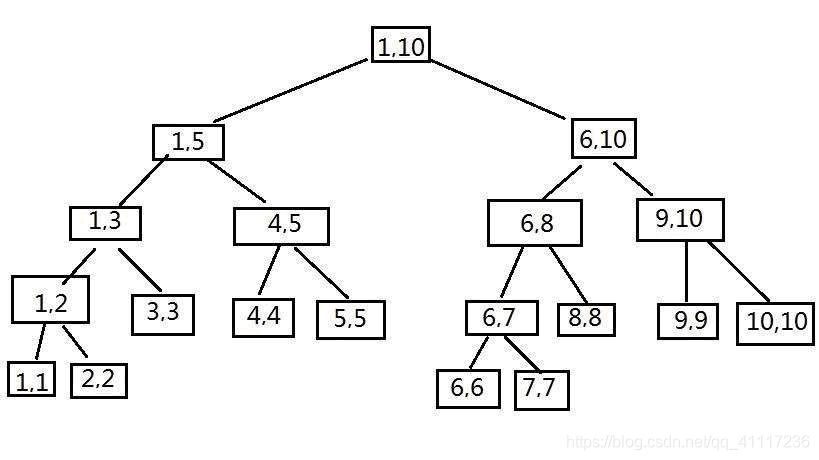
首先线段树的每个结点的实际意义是一个区间,每个结点的子节点是对该结点的一个等分。
即对每个内部节点 [l , r],令mid=(l+r)/2,它的左子节点是[l , mid],右子节点是[mid+1 , r]。
problem 1:求区间的最大值
题意:给定一个 n 位数组和对数组进行n次操作:
操作1:修改数组中某个位置的值
操作2:查询数组中某个区间的最大值
这个题如果要暴力去做的话 那么两个操作都是线性级别的 n次操作算法的时间复杂度就是O(n2) 显然付出的时间代价是比较高的,接下来我们试试考虑把区间划分,
使用线段树去维护数组信息。
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 1e5 + 5; struct SegmentTree { int l, r; int dat; } t[N * 4]; //用结构体数组存储线段树各个节点(区间左端点l、右端点r,区间信息dat) 线段树开节点n的四倍空间的证明这里不再赘述 int a[N]; //递归建立线段树 void build(int p,int l,int r) { t[p].l = l, t[p].r = r; //节点p代表区间[l,r] if (l == r) { //l==r时为叶子节点 叶子节点的区间l==r 且信息就是原数组的a[l](a[r]) t[p].dat = a[l]; return; } int mid = (l + r) / 2; build(p * 2, l, mid); //左子节点[l,mid] 编号p*2 build(p * 2 + 1, mid + 1, r);//左子节点[mid+1,r] 编号p*2+1 //核心操作写在递归语句之后意为递归到叶子节点后返回时操作 //因为这里先修改叶子节点才能修改上面大区间的节点哦 t[p].dat = max(t[p * 2].dat, t[p * 2 + 1].dat); } //对线段树的修改 void change(int p, int x, int v) { if (t[p].l == t[p].r) { //叶子节点l==r 递归到叶子节点直接修改 t[p].dat = v; return; } int mid = (t[p].l + t[p].r) / 2; if (x < mid) change(p * 2, x, v); //x在左半区间 else change(p * 2 + 1, x, v); //x在右半区间 //从下往上传递信息 t[p].dat = max(t[p * 2].dat, t[p * 2 + 1].dat); } //对线段树的查询 int ask(int p,int l,int r) { if (l <= t[p].l && r >= t[p].r) //递归到这个节点时要查询的区间被该节点完全包含 直接返回 return t[p].dat; int mid = (t[p].l + t[p].r) / 2; int val = -(1 << 31); //负无穷大 if (l <= mid) val = max(val, ask(p * 2, l, r)); //左子节点有重叠 if (r > mid) val = max(val, ask(p * 2 + 1, l, r)); //右子节点有重叠 return val; }
//查询简单来讲就是把要查询区间分成线段树x个节点中包含的区间 再递归更新最大值 signed main() { int n, m; scanf("%lld %lld", &n, &m); //原数组的长度和要询问的次数 for (int i = 1; i <= n; i++) { scanf("%lld", &a[i]); } build(1, 1, n); for (int i = 1; i <= m; i++) { int op,x, y; scanf("%lld %lld %lld", &op, &x, &y); if (op == 1) change(1, x, y);//单点修改 if (op == 2) printf("%lld\n",ask(1, x, y));//区间查询 } }
add:由于找不到oj的原题 代码没有测试 相似的题修改一下是过了的。。。。
时间复杂度分析(就简单提一下 深入分析可能篇幅较长)(后期会更新时间复杂度的证明):
1.单点修改 由于是二叉树 单点修改具体来说遍历就是一条路径 那么就是对数级别的O(logn)
2.区间查询 查询时会把区间成logn个节点 具体证明不再赘述 时间复杂度度O(logn)
所以总的时间复杂度就是O(nlogn)
problem 2 : 区间求和
你有N个整数,A1,A2,...,AN。您需要处理两种操作。
一种类型的操作是在给定的时间间隔内向每个数字添加一些给定的数字。另一种操作是询问给定间隔内的数字总和。
和problem 1类似 但在区间修改指令中 如果某个节点被修改区间[l , r]完全覆盖,那么以该节点为根的整颗子树中的所有节点存储的信息都会发生变化若逐一进行更新 使得时间复杂度度达到O(n),这是我们不能接受的。
这里我们要明白的是 若我们逐一更新了子树p的所有节点 但在查询指令中却根本不需要[l , r]的子区间作为候选答案那么更新子树p的所有子节点就是做了无用功的
我们引出懒标记(也称延迟标记)的方法 即当我们执行修改指令时,可以在l<=pl<=pr<=r时立即返回,在回溯之前向节点p增加一个懒标记 标记“该节点曾经被修改,但其子节点并未更新”
如果在后序的指令中 需要从节点p向下递归 再检查p是否有标记 如果有标记就根据标记信息更新p的两个子节点同时为p的两个子节点增加标记 然后清除p的标记 这样查询和修改的时间复杂度都为O(logn) (时间复杂度具体证明略 后期有机会补充)
这种”延迟“也是设计算法与解决问题一个重要思路
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 1e5 + 5; struct node { int l, r; int lazy;//懒标记(延迟标记)—lazy int sum; }T[N * 4]; int n, m, a[N]; void pushnow(int p, int v) { T[p].sum += (T[p].r - T[p].l + 1) * v; T[p].lazy += v; } //递归向下更新 void pushdown(int p) { if (T[p].lazy) { pushnow(2 * p, T[p].lazy); //更新左子节点 给左子节点打懒标记 pushnow(2 * p + 1, T[p].lazy); //更新右子节点 给右子节点打懒标记 T[p].lazy = 0; //清除当前的懒标记 } } void build(int p, int l, int r) {//建树 T[p].l = l; T[p].r = r; if (l == r) { T[p].sum = a[l]; T[p].lazy = 0; return; } int mid = (l + r) / 2; build(2 * p, l, mid); build(2 * p + 1, mid + 1, r); T[p].sum = T[2 * p].sum + T[2 * p + 1].sum;//回溯时向上传递信息(区间和) 即向上更新 } //线段树的更新 void update(int p, int ql, int qr, int v) { if (ql <= T[p].l && T[p].r <= qr) { pushnow(p, v); //当目标区间把节点区间包含在内时 更新当前节点并打懒标记 return; } int mid = (T[p].l + T[p].r) / 2; pushdown(p); //递归向下更新 if (ql <= mid) update(2 * p, ql, qr, v); if (qr > mid) update(2 * p + 1, ql, qr, v); T[p].sum = T[2 * p].sum + T[2 * p + 1].sum;//回溯时向上传递信息(区间和) 即向上更新 } //线段树的查询 int ask(int p, int ql, int qr) {//区间求和 if (ql <= T[p].l && qr >= T[p].r) return T[p].sum; //如果目标区间把该节点的区间包含在内直接返回 pushdown(p); //递归向下更新 int mid = (T[p].l + T[p].r) / 2; int ans = 0; if (ql <= mid) ans += ask(2 * p, ql, qr); if (qr > mid) ans += ask(2 * p + 1, ql, qr); T[p].sum = T[2 * p].sum + T[2 * p + 1].sum;//回溯时向上传递信息(区间和) 即向上更新 return ans; } signed main() { scanf("%lld %lld", &n, &m); for (int i = 1; i <= n; i++) scanf("%lld", &a[i]); build(1, 1, n); for (int i = 1; i <= m; i++) { int p; scanf("%lld", &p); if (p == 1) { int x, y, k; scanf("%lld %lld %lld", &x, &y, &k); update(1, x, y, k); } if (p == 2) { int x, y; scanf("%lld %lld", &x, &y); printf("%lld\n", ask(1, x, y)); } } }
problem 3:2022 年第四届湖北省ccpc大学生程序设计竞赛
L - Chtholly and the Broken Chronograph
Chtholly gives you an array of n elements, the i-th of which is ai .Each element in the array has an independent state si , where si = 0 denotes the i-th element is blocked, and si = 1 denotes it is activated. In order to maintain the array, Chtholly needs you to perform q operations, and there are four kinds of them:
1 x: Block element x, i.e. change sx to 0. It’s guaranteed that the element is activated before the operation.
2 x: Activate element x, i.e. change sx to 1. It’s guaranteed that the element is blocked before the operation.
3 l r x: Add x to each activated element in interval [l, r], i.e. for each i such that l ≤ i ≤ r and si = 1, assign ai + x to ai .
4 l r: Print the sum of elements in interval [l, r]. Note that this operation is irrelevant to the current states of elements.
Input
The first line of the input contains two integers n, q (1 ≤ n, q ≤ 105 ).
The second line contains n integers, the i-th of which is ai (1 ≤ ai ≤ 108 ).
The second line contains n integers, the i-th of which is si (si ∈ {0, 1}).
The next q lines, each line describe an operation. The forms of the operations are described in the statements above.
It is guaranteed that for each operation of type 3 or 4, 1 ≤ l ≤ r ≤ n, and for each operation of type 3, 1 ≤ x ≤ 108 .
Output
For each operation of type 4, output one line containing the answer.
Example:
standard input standard output
4 8 4 17
4 2 5 3 19
1 0 0 1
2 3
3 1 4 1
1 3
4 1 4
1 1
2 2
3 1 3
2 4 1 4
这个题只需要在problem 2的基础上加一个cnt 记录每个节点区间中启用的个数就可以了 需要写两种修改操作 一种是修改启用情况 一种是修改值
(大概就是在比赛中比签到题难一点点的那种题。。。。)
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 1e5 + 5; struct SegmentTree { int l, r; int cnt; //多加一个变量记录启用个数 int sum, lazy; }t[N * 4]; int n, q, a[N], s[N]; inline void pushup(int u) { t[u].sum = t[u * 2].sum + t[u * 2 + 1].sum; t[u].cnt = t[u * 2].cnt + t[u * 2 + 1].cnt; } inline void pushdown(int u) { t[u * 2].sum += (t[u * 2].cnt * t[u].lazy); t[u * 2 + 1].sum += (t[u * 2 + 1].cnt * t[u].lazy); t[u * 2].lazy += t[u].lazy; t[u * 2 + 1].lazy += t[u].lazy; t[u].lazy = 0; } inline void build(int u, int l, int r) { if (l == r) { t[u] = { l,r,s[r],a[r],0 }; } else { t[u] = { l,r,0,0,0 }; int mid = (l + r) / 2; build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r); pushup(u); } } inline int ask(int u, int l, int r) { if (t[u].l >= l && t[u].r <= r) { return t[u].sum; } pushdown(u); int mid = (t[u].l + t[u].r) / 2; int sum = 0; if (l <= mid)sum += ask(u * 2, l, r); if (r > mid)sum += ask(u * 2 + 1, l, r); return sum; } inline void change1(int u, int l, int r, int v) { if (t[u].l >= l && t[u].r <= r) { t[u].sum += (t[u].cnt * v); t[u].lazy += v; } else { pushdown(u); int mid = (t[u].l + t[u].r) / 2; if (l <= mid) change1(u * 2, l, r, v); if (r > mid) change1(u * 2 + 1, l, r, v); pushup(u); } } inline void change2(int u, int x, int v) { if (t[u].l == x && x == t[u].r) { t[u].cnt = v; s[x] = v; } else { pushdown(u); int mid = (t[u].l + t[u].r) / 2; if (x <= mid)change2(u * 2, x, v); else change2(u * 2 + 1, x, v); pushup(u); } } signed main() { cin >> n >> q; for (int i(1); i <= n; i++)scanf("%lld", &a[i]); for (int i(1); i <= n; i++)scanf("%lld", &s[i]); build(1, 1, n); while (q--) { int l, r, cz; int x; scanf("%lld", &cz); if (cz == 1) { scanf("%lld", &x); if (s[x] == 1) change2(1, x, 0); } else if (cz == 2) { scanf("%lld", &x); if (s[x] == 0) change2(1, x, 1); } else if (cz == 3) { scanf("%lld %lld %lld", &l, &r, &x); change1(1, l, r, x); } else { scanf("%lld %lld", &l, &r); printf("%lld\n", ask(1, l, r)); } } }
problem 4:(努力更新中)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号