代码源挑战赛 round 5
T1
给定整数 \(N\) ,用 # 画一个空心正方形。
\(3 \leq N \leq 100\)
思考:
我们分 \(1,N\) 和 \(2,3, \cdots, N-1\) 讨论一下。
官方题解:
和我一样的,一般来说分类越清晰越好,想一步写完不是做不到,就是很蠢。
T2
求 \(N\) 的第二大质因数。如果 \(N\) 的质因数不足 \(2\) 个,输出 \(-1\) 。比如 \(N = 150\) ,他的质因数有 \(\{ 2,3,5 \}\) 三个,其中第二大的是 \(2\) 。
\(2 \leq N \leq 10^{6}\)
思考1:
若 \(N\) 是素数当且仅当它只有一个素因子?
否则我们可以线性预处理 \(p1(x) \ s.t. 2 \leq x \leq N\) ,然后让 \(x\) 把 \(pmi(x)\) 扬掉。看起来是 \(O(N) \sim O(\log N)\) 。
注意:
让 \(x\) 扬掉 \(pmi(x)\) 的时候把 \(pmi(x)\) 预先拿出来,否则动态的 \(pmi(x)\) 一直是动态的 \(x\) 的最小素因子。
hack1:
若 \(N\) 是素数幂,他也只有一个因子。应该只露了这个条件吧,归纳一下确实只漏了这个条件。所以 \(N \geq 2\) 只有一个素因子当且仅当 \(N\) 是素数幂。(幂次大于等于 \(1\) 。)
思考2:
我们让 \(x\) 扬掉 \(p1(x)\) 后,看 \(x^{'} = x / pmi(x)\) 是否依旧是合数。如果是,则它不是素数幂。
于是不论是素数还是合数,我们总让 \(x^{'} = x / pmi(x)\) 检查 \(pmi(x^{'}) \neq 1\) 。
hack2:
\(330 = 2*3*5*11\) ,但是标准输出是 \(5\) 。
所以第二大是除了最大的次大,而不是除了最小的次小。
思考3:
我记得我们可以递推出 \(pmx\) ,而且应该不 dirty work 。想一下应该是
这里 \(p\) 是 \(n\) 的任意一个素因子,我们可以不妨让 \(pmi(n)\) 做这个 \(p\) 。想了一下这个递推式没啥问题。
然后将思考 \(2\) 里的 \(pmi\) 换成 \(pmx\) 应该就是问题的答案了。
hack3:
数据提示我需要输出 \(-1\) 的时候输出了 \(0\) 。想到我喜欢钦定 \(pmi(1)=1\) 是学老师的,但之前不知道为什么。只以为是在很多很多年前 \(1\) 被钦定为素数的缘故。
注意到我们之前检查 \(pmi(x^{'})\) 是否为 \(1\) ,当且仅当 \(x^{'}=1\) 才会触发这个情况。否则 \(x^{'}\) 总是还存在素因子。所以也有这个缘故。
而我只递推了 \(pmx(2 \cdots UP\_BOUND)\) 然后我把 \(pmx(1)\) 钦定为 \(1\)是不是就对了?确实对了。
时间复杂度 \(O(N) \sim O(\log N)\) 。
猜测,怎么感觉官方题解没这么复杂?
官方题解:
我擦,官方题解直接 \(O(N \sqrt{N})\) 分解质因数,按唯一分解定理的形式表示。若 SZ(v) < 2 就 -1 ,否则 v[tot-1] 就答案了。
T3
定义数组众数为其中出现次数最多的数字(一个数组的众数不一定只有一个)。
给定一个长度为 \(N\) 的整数数组 \(A\) ,现有另一个长度为 \(N\) 的数组 \(B\) ,其中 \(B_{i}\) 为数字 \(A_{i}\) 在 \(A\) 中的出现次数,求 \(B\) 的众数。如果有多个,输出最大的众数。
比如 \(A = \{ 1,2,2,4,2,4,3,3 \}\) ,\(B = \{ 1,3,3,2,3,2,2,2 \}\) ,所以 \(B\) 的众数为 \(2\) 。
\(1 \leq N \leq 10^{6}\) ,\(1 \leq A_{i} \leq 10^{7}\)
思考:
看起来可以开 \(1E7\) 的数组,我们开一个 \(cnt\) 当计数器。遍历 \(A\) 维护 \(cnt(A_i)\) 。然后遍历 \(1 \sim N\) 让 \(B_i = cnt(A_i)\) ,看起来就得到了 \(B\) 数组。
然后看起来把 cnt 清空一下,再对 \(B\) 数组计数一下,维护中间的最大计数更新众数。如果存在相同的计数,则钦定更大值是众数。看起来就行了?确实对了。
开桶的时间是固定 \(1E7\) 的,用 map 可以做到 \(O(N \log N)\) 。
官方题解:
T4
给定变异参数 \(M\) ,定义对数字 \(x\) 进行一次“变异”操作:将 \(x\) 变为 \(x\) 的每一位上的数字加起来加 \(M\) 得到的新数字。比如当 \(M=2\) ,\(315\) 进行一次变异的结果为 \(3 + 1 + 5 + 2 = 11\) 。
求对数字 \(N\) 进行 \(K\) 次变异操作后的结果。
\(1 \leq N \leq 10^{10^{5}}\) ,\(0 \leq M \leq 10^{6}\) ,\(1 \leq K \leq 10^{18}\) 。
思考:
如果不加上 \(M\) ,那么 \(N\) 就会按照 \(\log N\) 的速度衰减直到一位数,这是十进制数很显然的结论。然后可以在 \(T(\log_2 10^{10^{5}})=O(10^{5})\) 时间内搞出来。
如果加上 \(M\) ,想不出来不太会啊。
提示:
函数映射。鸽笼原理。
主要是题解给完提示后,依旧把做法讲出来了……直接看题解吧。
看完题解后自己的思考:
先分析一下题目,\(N\) 每次变成数位和后加上 \(M\) ,是先变小再变大,而且不能保证变异过程是有限次的。看起来不是很可控。
但注意到,可以找到所有变异数能够落在变异值域一个上下界,又稍微可控一点了。
对于一开始的 \(N\) ,很大,我们肯定用字符串读,但是一次编译后,最坏就是 \(1E5\) 个 \(9\) ,一次变异后就成了 \(\leq 9 \times 10^{5}\) ,再加上 \(M\) ,那么结果也是 \(< 2 \times 10^{6}\) 。我们声称这是变异值域的一个上界。于是我们让 \(N\) 等于变异一次后的数,再让 \(K-=1\) 。以后的所有数据范围都是在整数范围内可做的,于是数据范围过大这个困难就解决了。(这里 \(K \geq 1\) 恒成立,否则我们在处理第一步操作前还要判断一次。)
非常关注一件事情:值域有上界 O(10^{6}),下界 \(1\) ,这意味着上下界能够钦定的值域不大。
注意另一件事情,不妨定义变异是 \(f\) ,那么 \(f(N) = \sum digt(N) + M\) 这是一个函数形式的单射。
单射函数 完全等价于 基环树
这个点我怎么没想起来,无语了,神仙。下面是一个单射函数的图表示
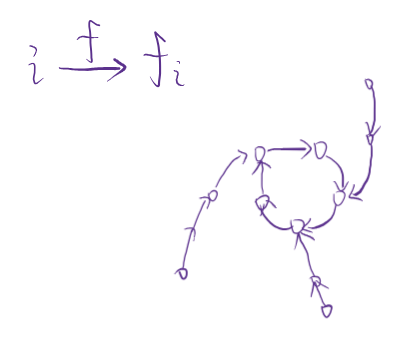
给一个奇怪的公式,让一个数变成另一个数。不在乎这个公式是什么,但这就是一个单射函数。
自然就知道了:单射+值域不大,天然是鸽笼原理能解决的问题。
鸽笼原理用在哪里?
- 可以保证不论这个基环树的形态怎么样,外面那些链的总长都不会超过值域给予的限制 \(UP\) ,否则他们应当进入循环。
- 可以保证,环长不会超过值域给予的限制 \(UP\) ,否则这个基环树不是单射函数的图。
对于基环树
我们总是容易找到环长 \(L\) 。然后让 \(K\) 尽可能的减去环长 \(L\) 但依旧大于链长。
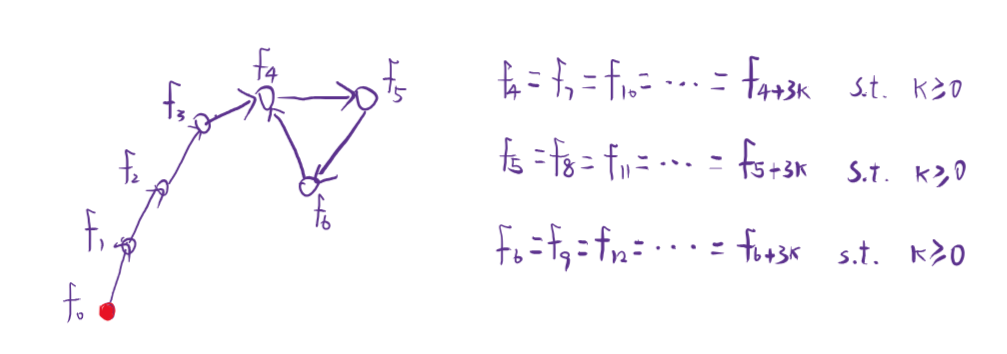
更深刻地说,在这类需要在基环树上沿着树边一步步走的问题上,实际上都会尽量避免找出它的链具体有多长,而是找一个肯定大于链长但能够被时间接受的长度 \(Q\) 。那么从起点往后走 \(K (K > Q)\) 步,时,就是 \((K-Q) \bmod L + Q\) 。有点类似暴力分治的概念。
- 换句话说,如果图太大,那凭借正常的输入方法也是没办法读入的。
- 除非单纯给出一个函数,在这里就是,完全不需要读入基环树,但是能给出基环树。
- 但是通常都是不需要真的找到每个链的真正长度的,那种问题难出现。
这里的值域限制是 \([1, 2 \times 10^{6}]\) ,给予的值域空间最多是 \(2 \times 10^{6}-1\) ,我们选择 \(Q=2 \times 10^{6}-1+1=2 \times 10^{6}\) 。
我们写一个 while 的死循环,从 \(N\) 开始(假设已经经过了第一次变异,下面的 \(N\) 都是经过第一次变异后的),记录 \(f*N\) 能到哪里,然后记录 \(f \circ f * N\) 能到哪里,……,最终当我们第二次访问到一个数的时候,就可以推出循环了。这个循环的时间复杂度是 \(O(M \varepsilon)\) 的。这里 \(2 \times 10^{6}\) 和 \(M\) 同阶,\(\varepsilon\) 是字符集大小,实际上是 \(\log_{10} 10^{6} = 6\) 。
我们通过 \(f\) 以 \(O(M)\) 的时间构造出了基环树。然后 \(f^{K}*N\) 就是可以倍增解决掉的。
如果这个 \(f\) 并不是简单的函数,而是具备平方的性质,即能得到 \(f \rightarrow f^{2} \rightarrow f^{4} \rightarrow f^{8}\) ,比如是一个置换群,则这个倍增就可以直接快速幂形式。时间复杂度即 \(O(M) \sim O(\log K)\) 。
可惜这里不是,我们只能真的在基环树上,用 \(O(M \log K)\) 的倍增去预处理 \(f^{X}*N\) ,然后也是用类似于快速幂的方法求答案。那么时间复杂度就是 \(O(M \log K) \sim O(\log K)\) 。看起来 \(10^{6}\) 带 \(\log\) 属于时间有点坏了。怎么感觉 \(w \times 10^{6} \times 10^{18} = 180 \times 10^{6}\) 能过是因为我的 ST 表卡 cash 非常高超?
挂了:
说说我哪里挂了。我们看
是单射。那么构造混循环的时候,实际上能发现,混循环拼接的地方存在 \(g=f(x)=f(y)\) 。
当确定了 \(g\) 被第二次访问,这个第二次访问要实现后才能推出循环,否则环没有被接起来就断开了。
更深刻地,只要记得找混循环的环的时候,在 \(break\) 之前再做一次 f[x]=work 操作即可。
更深刻地,并查集并到一起的时候,就是我们第一次访问到一个同样的点。这时候我们方便选择在 break 前操作或不操作。如果这个点已经访问到了,那么整个混循环的 \(f\) 也连上了。
总结了一些倍增的小细节:
- 区间倍增是要很关注边界的,并不存在点合不合法的说话。
- 树上或基环树的倍增主要关注点是不是合法的,而不那么需要关注边界。
- 让 \(logK\) 直接对 \(K\) 取 \(\log_2 K\) 下取整就行了
- 一码归一码,区间倍增的查询就是你想的那样。
- 能直接快速幂的话也是你想的那样。
- 树上倍增通常用不到 \(f(0,x)\) ,这个数做不了倍增的贡献,奈何答案可能会问,所以有时候一开始也要处理出来。
- 我们会去处理开始的 \(f(1,x)\) 以用于对倍增贡献
- 树上倍增,我们得到答案后可以用类似快速幂的形式找答案。但很坑的是幂次上第 \(i\) 位(从 \(0\) 开始)实际上是往上跳 \(i+1\) 步。
- 再总结一下,幂次上第 \(i\) 位,在区间倍增的询问里是 \(2^{i}\) 大小的区间,在树上倍增的询问里是往上跳 \(i+1\) 步。
- 类似快速幂的写法,写起来像是 ksm(N,K): res=N; L(i,1,logM)if(X&bitl(i-1))res=f[i][res];
然后其实这种题我没写过,纯口嗨乱调很痛苦才调对的,这里需要放一下代码。(没办法我纯纯码力低能儿,写什么都靠现编,我只有加训而已)
view
const int MAXN=2000005;
int f[MAXN],fa[MAXN];
const int logM=60;
int go[61][MAXN];
string str;
i64 N,M,K;
int find(int x){ return x==fa[x]?x:fa[x]=find(fa[x]); }
signed main(){
cin.tie(nullptr)->ios::sync_with_stdio(false);
rd(str,M,K);
K-=1, N=M; L(i,0,SZ(str)-1)N+=(str[i]-'0');
auto work=[&](int x)->int{
int res=M;
while(true){
res+=x%10;
if((x/=10)==0)break;
}
return res;
};
const int UP=2000000;
L(i,1,UP)fa[i]=i;
L(i,1,UP)if(find(i)==i){
go[0][i]=i;
int x=i;
int u=find(x);
while(true){
x=go[1][x]=f[x]=work(x);
int v=find(x);
if(u==v)break;
fa[v]=u;
}
}
L(i,2,logM){
L(j,1,UP)if(go[i-1][j]!=0){ // 这个合法状态的判断还是非常有必要的
go[i][j]=go[i-1][go[i-1][j]];
}
}
auto ksm=[&](int N,i64 X){ int res=N; L(i,1,logM)if(X&bitl(i-1))res=go[i][res]; return res; };
wrn(ksm(N,K));
return 0;
}
再想一想,如果倍增是好的,那这题是不是可以多次询问?因为给出的 \(N\) 经过一次变异后 \(\leq 9 \times 10^{5} + M \leq 2 \times 10^{6}\) 。单射函数在一个区间内,能够得到若干个环、混循环、链,不妨都叫做他们是循环。我们可以遍历 \(1 \sim 2 \times 10^{6}\) ,可以线性地把所有循环都构造出来,因为每个点至多被访问两次。
但注意到对于每个 \(\leq 10^{10^{5}}\) 的 \(N\) ,我们都需要先让它暴力地进行一次变异,然后 \(N\) 才会不超过上界,这个暴力是 \(O(10^{5})\) 且对询问做贡献的。\(q\) 次询问会使得 \(O(M \log \varepsilon) + O(M \log K) \sim O(\log K)\) 变成 \(O(M \log \varepsilon) + O(M \log K) + q(M + \log K)\) 。所以若要多次询问,则开始的 \(N\) 不能很大。这等于减少了一个重要的考察知识点,增添了一个无关紧要的考察知识点。
官方题解:
主播主播,\(O(N \log K) \sim O(\log K)\) 的倍增算法虽然又易懂又暴力又能卡 cash,但还是太慢了。有什么理论上很快的写法?
官方题解说的让 \(N\) 第一次变异,以及通过上下界和鸽笼原理确定混循环,这里就跳过了。问题是之后的算法。
官方是把循环节找出来,然后让 K 模循环节的长度,然后问题就约束到了 \(O(M)\) 级别。然后这个找循环节是很有手法的。要学。
找完循环节之后呢,直接暴力冲过去就完了。
分析1:
如果 \(K = 10^{10^{5}}\) ,那你 byd 是不是有 \(\log_ K = log_{2} 10^{10^{5}} \sim 10^{5} \times 3 / 10 = O(10^{5})\) ?给你直接上来一个 \(O(M \log K) = O(10^{6} \times 10^{5}) = O(10^{11})\) 神仙也顶不住。
那这个时候,我们是不是想办法找到 \(N\) 所在循环的那个循环节,然后搞一个高精度取模。然后就很爽的把时间复杂度降到了 \(O(M \log M) \sim O(\log M)\) 。
分析2:
官方题解说,我们可以设计一个时间戳 \(vis\) ,\(vis(N)=1\),\(vis(f*N)=2\) ,然后 \(vis(f \circ f * N) = 3\) ,\(vis(f^{3}) * N = 4\) ,……。直到 \(f*x \neq 0\) ,说明下一次我们就接上混循环了。假设当前时间是 \(T\) ,那么混循环中那个圈的大小就是 \(r=T-vis(f*x)+1\) (毕竟是当作一条链算的长度)。最后讲课人(ljr?)说把 \(K\) 模掉 \(r\) 就行了?
这里看起来应当是显然有点问题的。事实上我们可以采取类似扩展欧拉定理的做法,取 \(Q=2 \times 10^{6}\) 。
好难调。
调死我了,我不能精确找到混循环将要拼接上和已经拼接上的时候的那个点。直接用并查集判当前是不是在一个集合中问题全解决了,我真的老实了。
利用 \(r\) 得到最小的等价 \(K\) 之后,这里就不打倍增了,直接冲暴力,因为这里利用了先变异一次 \(N\) 的技巧,所以是单次询问,这样的话是比倍增快的。
下面再给一发代码,因为类似的代码我没写过(先写,还不一定对)。一写,果然痛苦地又调了好久。
下面说并查集维护 \(r\) 数组的一些注意点,或者说我以前是不是根本就不会并查集维护集合权值?
- 在找 \(r\) 的时候,如果是第一次确定出了 \(r\) ,肯定是对的。因为第一次就能找出混循环的环。
- 详细地说,当找到环时候, \(r(find(x)) \neq 0\) ,我们对 \(r\) 赋值。
- 如果不是第一次找到环,可能会从混循环的链找到环,这也是在判断到了一些点同一个并查集中,但是这时候不能更新 \(r\) 。
- 而这时候需要合并纯循环的两个部分,让他们有同一个代表元。只有一个代表元所在的集合有环。
- 所以合并代表元 v 连向代表元 u 的时候,若 v 有环,还需要 \(r(u)=r(v)\) 。
view
const int MAXN=2000005;
int f[MAXN],fa[MAXN],vis[MAXN],r[MAXN];
string str;
i64 N,M,K;
int find(int x){ return x==fa[x]?x:fa[x]=find(fa[x]); }
signed main(){
cin.tie(nullptr)->ios::sync_with_stdio(false);
rd(str,M,K);
K-=1, N=M; L(i,0,SZ(str)-1)N+=(str[i]-'0');
auto work=[&](int x)->int{
int res=M; while(true){
res+=x%10;
if((x/=10)==0)break;
}
return res;
};
const int UP=2000000;
L(i,1,UP)fa[i]=i;
L(i,1,UP)if(find(i)==i){
int x=N;
int u=find(x);
int T=0;
vis[x]=++T;
while(true){
x=f[x]=work(x);
int v=find(x);
if(u==v){
if(!r[u])r[u]=T-vis[x]+1;
break;
}
if(r[v])r[u]=r[v];
fa[v]=u;
vis[x]=++T;
}
}
if(K>UP)K=(K-UP)%r[find(N)]+UP;
L(i,1,K)N=f[N];
wrn(N);
return 0;
}
高精度对低精度取模?
虽然没写过,但是原理很简单啊。利用 \((x \times y + z) \bmod m = ((x \times y \bmod m) + y) \bmod m\) 。我们把大数看成多项式,就可以线性地高精度取模。
N=0; L(i,0,SZ(str)-1) N=(N*10+(str[i]-'0'))%MOD;
N 开 long long 就可以不用中间再取模。64 位现在基本上都是比取模快很多的。
T5
给定正整数 \(N\) ,求 \(N\) 对 \(1 \sim N\) 取模的余数之和,即 \(\sum_{i=1}^{N}(N \bmod i)\) 。
\(1 \leq N \leq 10^{9}\)
思考:
手玩乱搞一下,可以把 \(\sum_{i=1}^{N}(N \bmod i)\) 化成 \(\sum_{i=1}^{N} (N - \lfloor \frac{N}{i} \rfloor i)\) ,然后就很显然了。然后实际上这个化简应该是个经典结论,应该刻意记一下,而不是临时手玩。
\(\sum_{i=1}^{N} N = N^{2}\) 可以 \(O(1)\) 算。我们主要算 \(\sum_{i=1}^{N} \lfloor \frac{N}{i} \rfloor i\) ,类似 \(\sum_{i=1}^{N} \lfloor \frac{N}{i} \rfloor f(i)\) 之类的公式总是可以数论分块,做到 \(O(\sqrt{N})\) 复杂度。
具体的,想一下 \(\sum_{i=1}^{N} \lfloor \frac{N}{i} \rfloor f(i)\) 的一段,假设 \(x=\lfloor \frac{N}{i} \rfloor\) ,\(i=l,l+1, \cdots, r\) ,我们要算的是 \(x \times f(l) + x \times f(l+1) + \cdots + x \times f(r) = x \times \sum_{j=l}^{r} f(j)\) ,所以我们要做的就是快速求 \(f(j)\) 的前缀和,但不能线性预处理 \(f\) (显然 \(O(N)\) 是超时的)。这里呢,\(f(N) = \sum_{i}^{N} i = \binom{N+1}{2} = \frac{N(N+1)}{2}\) 可以 \(O(1)\) 求,这就很好。
通常我们会把 \(i\) 看成 \(l\) 去遍历。其中 \(x = \lfloor \frac{N}{l} \rfloor\) 是好算的,其实不难证明 \(r=\lfloor \frac{N}{x} \rfloor\) ,然后让 \(r=l\) 。这些 \((l,r)\) 总共会有 \(O(\sqrt{N})\) 段。对于每一段,我们去算 \(x \times (f(r) - f(l-1)) = x(\frac{r(r+1)}{2} - \frac{(l-1)l}{2})\) 就行了。
hack:
真行了嘛?怎么我算的 \(\sum_{i=1}^{N} \lfloor \frac{N}{i} \rfloor i\) 比 \(N^{2}\) 还大?
我首先给 \(i=l,r. x = \lfloor \frac{N}{i} \rfloor\) 打印了出来,发现没有任何问题。
然后检查了一下变量类型,都是 i64 的。
然后我继续打印,发现 \(f(l\) 爆了,而 \(f(r)\) 没爆。于是一个正数减去负数肯定会变得很大。
然后我意识到了,我的 L(i,a,b) 是 int 的 i 。一个改进是,i64 l=i ,而且这个改进其实很科学。注意最后让 i=r 而不是 l=r 。
然后我对了。
官方题解肯定是和我一样的,这个问题应该(大概率)没有其他比较轻松的做法,没必要看了。
T6
有 \(N\) 个知识点,第 \(i\) 个知识点的价值为 \(A_i\) ,复习难度为 \(B_i\) ,遗忘度为 \(C_i\) 。
复习知识点所花费的时间与复习顺序有关,具体来说,如果第 \(i\) 个知识点被排在第 \(j\) 位复习,那么需要花费 \(B_i + j \times C_i\) 的时间。
求花费时间不超过 \(T\) 的前提下,恰好复习 \(m\) 个知识点的最大价值和。
如果无法在 \(T\) 时间内复习 \(M\) 个知识点,输出 \(-1\) 。
第一行包括三个正整数 \(N,M,T\) ,分别表示知识点数量、需要复习的知识点数量和时间限制。
第二行包括 \(N\) 个正整数 \(A_i\) ,分别表示每个知识点的价值。
第三行包括 \(N\) 个正整数 \(B_i\) ,分别表示每个知识点的难度。
第四行包括 \(N\) 个正整数 \(C_i\) ,分别表示每个知识点的遗忘度。
\(1 \leq M \leq N \leq 40\) ,\(0 \leq T \leq 10^{18}\) ,\(1 \leq A_i \leq 10^{15}\) ,\(0 \leq B_i,C_i, \leq 10^{15}\) 。
思考1:
因为看到 \(m \leq n\) 感觉可以把 \(m\) 这一维 dp 出来,比如尝试考虑了 i 的前缀选了 j 个的最大价值。然后发现物品能选择的顺序很奇怪,看起来又不是 dp 。
不会了,给我这个小范围的数据我也不知道怎么做啊。硬要说,我能 \(O(N!)\) 的方法冲出所有的 \(n\) 的 \(m\) 排列骗个 \(N \leq 8\) 的数据分。
提示1:
能不能用 \(2^{n}\) 的方法骗到 \(n \leq 20\) 的数据分?
思考2:
要求确定一个最好的 \(m\) 排列,是这个排列的代价不超过 \(T\) ,同时这个排列的价值最大?没见过这种问题啊。给这个提示我也不会啊。
提示2:
如果已经确定复习哪 \(m\) 个知识点,能得到的价值固定。如何复习能让复习这些知识点的总代价(总花费时间)最小?
思考3:
第 \(i\) 个知识点放在第 \(j\) 位复习,花费的时间是 \(B_i + j \times C_i\) 。我们总是可以直接把代价 \(B_i\) 算在一起,然后要考虑的就是 \(j \times C_i\) 怎么安排能让代价最小?这玩意的偏序是 \(j \times C_{k}, (j+1) \times C_{k+1}\) ?好像不可控?这种下标确实不可控。但如果我说,把 \(C_i\) 越高的放在越前面呢,是不是 \(j \times C_{i}\) 是个很经典的被证明过的贪心排布?好像是的。
所以可以 \(2^{m}\) 这样去枚举子集,可以直接算出每个子集的价值。对每个子集,我们按照 \(C_i\) 最大的顺序给他钦定顺序,再带一个排序的时间,代价也算出来了。于是我们每个最优子集都搞定了。总的花费时间是 \(O(2^{n} n \log n)\) ?
然后你是真的蠢,既然你每次选完一个子集,再把 \(\{C\}\) 按从大到小排序,为什么不一开始就把 \(\{C\}\) 排序?这样花费时间就是 \(O(2^{n} n + n \log n)\) 的。
冲一发代码大概是下面这个样子。
然后期间也调得很痛苦……为什么,因为 for 的 int(i) 直接按 longlong 做乘法了…… 各种 longlong 的变量和数组都开成 int 了……
view
const int MAXN=45;
int N,M;
int p[MAXN];
i64 T,m,ans,res,cost;
i64 A[MAXN],B[MAXN],C[MAXN];
signed main(){
cin.tie(nullptr)->ios::sync_with_stdio(false);
rd(N,M,T);
L(i,1,N)rd(A[i]);
L(i,1,N)rd(B[i]);
L(i,1,N)rd(C[i]);
L(i,1,N)p[i]=i;
assert(N<=20);
sort(p+1,p+N+1,[&](int i,int j){
return C[i]>C[j];
});
m=bit(N);
ans=-1;
L(mask,1,m-1)if(__builtin_popcount(mask)==M){
res=0,cost=0; VI vec{0};
L(i,1,20)if(mask&bit(i-1))vec.psb(p[i]);
assert(SZ(vec)-1==M);
L(i,1,M){
res+=A[vec[i]];
cost+=B[vec[i]];
cost+=1LL*i*C[vec[i]];
}
if(cost<=T)chkmax(ans,res);
}
wrn(ans);
return 0;
}
好,现在 \(N \leq 20\) 的数据是高过去了。怎么搞过 \(N \leq 40\) 的数据呢?
提示3:
如果枚举出了两个不相交的子集,并确定了这两个子集的最优排列后,这两个子集的贡献能不能快速合并?
思考4:
对于子集 \(\mathbb{S}_1,\mathbb{S}_2\) ,当已经确定了他们的最优排列后,\(\{A\}, \{B\}\) 的贡献都可以直接 \(O(1)\) 合并。至于 \(\{C\}\) 的贡献,如果是 \(\mathbb{S}_2\) 的最优排列接在 \(\mathbb{S}_1\) 的最优排列后,那么 \(\mathbb{S}_2\) 的 \(j \times C_i\) 就要变成 \((j+|\mathbb{S}_1|) \times C_i\) ,换句话说即是在原基础直接加上 \(|\mathbb{S}_1| \times C_i\) 。如果预处理好 \(C_i\) 的和,这里也可以做到 \(O(1)\) 合并。
这样的话我们可以按 \(O(n 2^{n})\) 的方法先处理前一半,对每个 \(mask\) 用哈希表存他的价值和代价。
再用 \(O(n 2^{n})\) 的方法处理后一半,正常算出价值和代价,包括 \(\sum C_i\) 。然后这时候是不是应该去哈希表中找一个子集,满足前后两个子集合并后代价不超过 \(T\) ,并且价值最大?但是这个好像没办法快速做到啊。然后我又不会了。
提示4:
为什么可以合并?因为选 \(M\) 个数是固定的。
思考5:
那么我乱搞去想合并完全是乱搞啊。我甚至不清楚为什么要合并,只关心如果能合并,那么时间可以压下去。
由于选 \(M\) 个数是固定的,所以才可以合并。这意味着我们处理后一半的时候是清楚自己选了 \(k\) 个数的,那么还剩 \(M-k\) 个数没选,就要去哈希表里找。所以实际上哈希表不应该按照 mask 当作主键存,而是应该按照 __builtin_popcount(mask) 当作主键存。
然后呢?好像又没办法了。我不知道怎么处理哈希表的 value 。
是应该存一个所有子集的最优排列吗?好像不是,很困难,找不到这种性质。
是应该存储一个 vector ,记录所有 __builtin_popcount(mask) 相同的子集的最优排列吗?但是即使这样,我们唯一能做的就是二分找到代价总和不超过 \(T\) 的区间,而价值和是否最大是没办法保证的。
所以又不会了。
提示5:
哈希表主键是选了 \(i\) 个(即 __builtin_popcount(mask)=i),值是所有 \(i\) 大小的前半集合的最优排列对应的价值和代价。具体的一个 \(hs(i)\) 对应一个 vector 。对 \(hs(i)\) 中的方案做删除,使得哈希表中剩余方案都是相同时间下得到最多价值的方案,并让时间按照递增排序。
思考6:
我擦这样好像就很牛逼了。我如果处理完了每个 \(hs(i)\) ,在确定了后半的 \(M-i\) 大的集合后,去 \(hs(i)\) 里二分最大的时间花费使得时间代价不超过 \(T\) ,比如这个位置是 \(k\) 。那么价值的 \(k\) \(max\) 前缀是不是就是最优的?
首先是对 \(hs(i)\) 的去重,怎么处理?想想好方法啊……我们是不是可以先做一个 map<pair<int,i64>,i64> ,key 是集合大小、时间组成的 pair ,value 是当前集合大小、花费当前时间的所有最优排列中,能得到的最大价值。我们对着相同的 key 更新最大 value 。最后遍历这个 map 去赋值所有 hs 数组就行。
再然后再对所有 hs 数组排个序,然后再求一遍前缀 \(max\) 赋值给价值。
然后这个双关键字二分又是很少写过的,假设当前有 \(cost\) ,我们要先找第一个大于 \(T-cost\) 的位置,那么要 upperbound 一个 pair 就是 \((T-cost,INFL)\) 。然后注意 upperbound 里不能传入 list ,要显示转化。
然后艰难的写了一发代码,居然超时了无语。反正复杂度按大 \(O\) 估计来算,估是估是估成 \(O(N_{1}2^{N_1} + N_{2}2^{N_2})\) 的。
复杂度差不多对但是被卡的代码
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
#define L(i,a,b) for(int i=(a);i<=(b);i++)
#define R(i,a,b) for(int i=(a);i>=(b);--i)
#define fi first
#define se second
#define y1 qnmlgb
#define psb push_back
#define ppb pop_back
#define ps push
#define pp pop
#define rvs reverse
#define ept empty
#define ist insert
#define ers erase
#define clr clear
#define SZ(x) int((x).size())
#define all(x) (x).begin(),(x).end()
#define cou(x) count((x))
#define VI vector<int>
#define VVI vector<VI>
#define bit(x) (1<<(x))
#define bitl(x) (1LL<<(x))
template<typename T> void rd(T &x){ cin>>x; }
template<typename T,typename... Args> void rd(T &x,Args&... args){ cin>>x; rd(args...); }
template<typename T> void wrn(T x){ cout<<x<<"\n"; }
template<typename T,typename... Args> void wrn(T x,Args... args){ cout<<x<<" "; wrn(args...); }
template<typename T> void wrl(T x,int i,int j){ cout<<x<<" \n"[i==j]; }
template<typename T> void crn(T x){ cerr<<x<<"\n"; }
template<typename T,typename... Args> void crn(T x,Args... args){ cerr<<x<<" "; crn(args...); }
template<typename T> void crl(T x,int i,int j){ cerr<<x<<" \n"[i==j]; }
template<typename T> void chkmax(T &x,T y) { x=x<y?y:x; }
template<typename T> void chkmin(T &x,T y) { x=x<y?x:y; }
const int INF=1<<29;
const i64 INFL=1LL<<61;
const int MAXN=45;
int N,M,N1,N2;
int p[MAXN];
i64 T,m1,m2,ans,res,cost,scost;
i64 A[MAXN],B[MAXN],C[MAXN];
vector<pair<i64,i64>> hs[MAXN];
map<pair<int,i64>,i64> mp;
signed main(){
cin.tie(nullptr)->ios::sync_with_stdio(false);
rd(N,M,T);
L(i,1,N)rd(A[i]);
L(i,1,N)rd(B[i]);
L(i,1,N)rd(C[i]);
L(i,1,N)p[i]=i,hs[i].clr();
mp.clr();
sort(p+1,p+N+1,[&](int i,int j){
return C[i]>C[j];
});
N1=N/2,N2=(N+1)/2;
m1=bit(N1),m2=bit(N2);
L(mask,1,m1-1){
int c=__builtin_popcount(mask);
VI vec{0};
L(i,1,N1)if(mask&bit(i-1))vec.psb(p[i]);
res=0,cost=0;
L(i,1,c){
res+=A[vec[i]];
cost+=B[vec[i]];
cost+=1LL*i*C[vec[i]];
}
if(cost<=T)chkmax(mp[{c,cost}],res);
}
for(auto info:mp){
auto key=info.fi;
i64 res=info.se;
int c=key.fi;
i64 cost=key.se;
hs[c].psb({cost,res});
}
L(i,1,MAXN){
sort(hs[i].begin(),hs[i].end());
i64 mx=0; for (auto &info:hs[i]){
auto &w=info.se;
chkmax(mx,w); w=mx;
}
}
ans=-1;
L(mask,1,m2-1){
int c=__builtin_popcount(mask);
VI vec{0};
L(i,1,N2)if(mask&bit(i-1))vec.psb(p[N1+i]);
res=0,cost=0,scost=0;
L(i,1,c){
res+=A[vec[i]];
cost+=B[vec[i]];
cost+=1LL*i*C[vec[i]];
scost+=C[vec[i]];
}
int k=M-c;
cost+=1LL*k*scost;
if(cost>T||c>M)continue;
auto it=upper_bound(hs[k].begin(),hs[k].end(),pair<i64,i64>{T-cost,INFL});
if(it!=hs[k].begin()){
it=prev(it);
res+=it->se;
cost+=it->fi;
assert(cost<=T);
}
chkmax(ans,res);
}
wrn(ans);
return 0;
}
注意点
- 第二段处理后 \(N_2\) 个数的时候,下标要加上 \(N_1\) 。因为我们是从 \(N_1 + 1\) 的位置开始处理的。
- 二分的时候,基本就是按 it 是不是 begin 和 end 考虑。
- 如果定位到 end 了基本都是没找到,有时候没找到是好的,不需要特殊处理。有时候没找到是不好的,需要特殊处理。具体情况冷静分析。
- 如果定位到了 begin ,找是找到了,但是有时候需要 prev(it) ,那这是需要讨论的。具体情况冷静讨论。
问题:
1. 很严肃的常数开销。
不要在循环中大量申请 vector 然后释放。
- 每次循环申请一个 vector 会反复地贡献构造和析构的开销。
- 每次循环清空 vecot 和上述方法是时间开销一样,但是只会有一次构造和析构的开销。
2. 相对严肃的常数开销。
需要大量申请的 vector ,如果有必要,可以尽量换成数组。这个常数会快很多,但是多数时候会让代码变成很难写。
3. 时间复杂度。
设 \(N=N_{1}+N_{2}\) ,我们分前后两段处理。
- 第一二段不算 map 和二分贡献,时间贡献为 \(T(N_{1} 2^{N_1} + N_{2} 2^{N_2})\)
- 第一段的 \(map\) 插入贡献和遍历贡献为 \(T(2 \times 2^{N_{1}} \log 2^{N_{1}})=T(2 \times N_{1} \times 2^{N_1})\) ,第二段的二分贡献会将 \(O(2^{N_1})\) 个元素被均摊到 \(1,2, \cdots, N_2\) 共 \(N_2\) 个部分以至于基本不是瓶颈。二分会被均摊这点很重要。
- 总结一下时间开销就是 \(T(N_{1} 2^{N_1} + N_{2} 2^{N_2} + 2 \times N_{1} \times 2^{N_2}) = T(4 \times N_{1} 2^{N_1} + N_{2} 2^{N_2})\) 。稍微让 \(N_1\) 的部分抖 \(1\) 或 \(2\) 到 \(N_2\) 显然是要更快的。
4. 时间复杂度。
用 dfs 代替枚举子集,可以优化一个 \(N\) 。但是 dfs 常数相对大。
可能还有其他很多优化。但是上面几个优化可能是最重要的。反正不想写 \(dfs\) ,下面的代码数据过是过了,把 vector 从多次申请改成了清空,分块稍微抖了一下,让 \(N_1\) 补了 \(2\) 到 \(N_2\) 。
过是过了的代码
const int INF=1<<29;
const i64 INFL=1LL<<61;
const int MAXN=45;
int N,M,N1,N2;
int p[MAXN];
i64 T,m1,m2,ans,res,cost,scost;
i64 A[MAXN],B[MAXN],C[MAXN];
vector<pair<i64,i64>> hs[MAXN];
map<pair<int,i64>,i64> mp;
VI vec;
signed main(){
cin.tie(nullptr)->ios::sync_with_stdio(false);
rd(N,M,T);
L(i,1,N)rd(A[i]);
L(i,1,N)rd(B[i]);
L(i,1,N)rd(C[i]);
L(i,1,N)p[i]=i,hs[i].clr();
mp.clr();
sort(p+1,p+N+1,[&](int i,int j){
return C[i]>C[j];
});
N1=N/2,N2=(N+1)/2;
N1-=2;N2+=2;
m1=bit(N1),m2=bit(N2);
L(mask,1,m1-1){
int c=__builtin_popcount(mask);
vec.clear();
L(i,1,N1)if(mask&bit(i-1))vec.psb(p[i]);
res=0,cost=0; assert(SZ(vec)==c);
L(i,1,c){
res+=A[vec[i-1]];
cost+=B[vec[i-1]];
cost+=1LL*i*C[vec[i-1]];
}
if(cost<=T)chkmax(mp[{c,cost}],res);
}
for(auto info:mp){
auto key=info.fi;
i64 res=info.se;
int c=key.fi;
i64 cost=key.se;
hs[c].psb({cost,res});
}
L(i,1,MAXN){
sort(hs[i].begin(),hs[i].end());
i64 mx=0; for (auto &info:hs[i]){
auto &w=info.se;
chkmax(mx,w); w=mx;
}
}
ans=-1;
L(mask,1,m2-1){
int c=__builtin_popcount(mask);
vec.clr();
L(i,1,N2)if(mask&bit(i-1))vec.psb(p[N1+i]);
res=0,cost=0,scost=0; assert(SZ(vec)==c);
L(i,1,c){
res+=A[vec[i-1]];
cost+=B[vec[i-1]];
cost+=1LL*i*C[vec[i-1]];
scost+=C[vec[i-1]];
}
int k=M-c;
cost+=1LL*k*scost;
if(cost>T||c>M)continue;
auto it=upper_bound(hs[k].begin(),hs[k].end(),pair<i64,i64>{T-cost,INFL});
if(it!=hs[k].begin()){
it=prev(it);
res+=it->se;
cost+=it->fi;
assert(cost<=T);
}
chkmax(ans,res);
}
wrn(ans);
return 0;
}
其实我觉得他都已经指数算法带个 \(N \leq 40\) 了,稍微多开 \(1s\) 应该是没啥问题的,但是我自己的代码常数确实一开始也有比较大的问题,特别是在循环里反复申请 vector 的解析和析构的开销过高。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号