MC 定理

其实是 \(Hall\) 定理，但 \(MC\) 条件对 \(Hall\) 来说是充要的。我更习惯说 \(MC\) 定理，更容易讨论充要条件。

1. MC 定理的基础应用

代数表示：对于一个集合族 \(\mathcal{A}=(\mathbb{A}_1,\mathbb{A}_2, \cdots, \mathbb{A}_n)\) ，\(\mathcal{A}\) 有 \(SDR\) \((w_1, w_2, \cdots, w_n)\) 当且仅当对于 \(k = 1,2, \cdots, n\) 且满足 \(1 \leq i_1 < i_2 < \cdots i_k\) 的每组 \(i_1, i_2, \cdots, i_k\) ，都有 \(|\mathbb{A}_{i_1} \cup \mathbb{A}_{i_2} \cup \cdots \cup \mathbb{A}_{i_k} | \geq k\) 。

图论表示：对于二分图 \(\mathbb{G} = \mathbb{V}_1, \mathbb{V}_2 \ s.t. \ |\mathbb{V}_1| \leq |\mathbb{V}_2|\) ，\(\mathbb{V}_1\) 有完备匹配当且仅当 所有 \(k=1,2, \cdots, |\mathbb{V}_1|\) 的 \(\mathbb{V}_1\) 的 \(k\) 子集 \(\mathbb{S}\) ，满足 \(|\mathbb{N}(\mathbb{S})| \geq |\mathbb{S}|\) 。

1.1 TCO 2015 1A Hard, Revmatching

http://oj.daimayuan.top/course/23/problem/1105
给一个完全二分图 \(\mathbb{K}_{n,n}\) ，每条边有边权 \(w\) 。求一个边权和最小的边集，使得 \(\mathbb{K}_{n,n}\) 删除该边集后不存在完备匹配。

题目会按照：

• \(i=1,j=1,2, \cdots, n\) ，
• \(i=2,j=1,2, \cdots, n\) ……
• \(i=n,j=1,2, \cdots, n\) 。

的形式给出左部点和右部点的边。

\(n \leq 20, w \leq 10^{12}\)

思考1：

看起来可能能用网络流做，可能是吧。但注意看起来是最小割，但是最大流最小割不太能处理带权二分图的匹配问题。看起来是费用流，但是费用流和最小割没有联系。

想想其他的。注意这个 \(n\) 可以用指数算法解决。引导我们朝着 SDR 的 MC 定理思考。

思考2：

\(O(2^{n})\) 确实可以做到枚举点集的幂集，根据推论甚至能判断最大具有 SDR 的子族。但是和这题有啥关系呢。好像没啥能继续推进的思路了。

思考3：

这里用到了 SDR 和 MC 的充要条件。枚举幂集，将当前子集的邻居，以任一一种方式，删到小于自己为止。具体的，删一个邻居会连带删除一条边。

这些删除方式的并，这不就找到了所有让二分图没有完备匹配的情况了吗。实际上，对于每个枚举到的子集，都存在一个最优的删除方式，即按边权从小到大删除。

于是我们枚举二分图的左部点的幂集的元素，对于每个子集，都存在唯一一种可能是最优解的删除方式。

枚举幂集的一个元素是 \(2^{n}\) 的，取所有邻居是 \(O(n^{2})\) ，删除是 \(O(n^{2})\) 的，需要排序是 \(O(n^{2} \log n^{2})\) 的，确定一个子集后瓶颈在于排序的 \(O(n^{2} \log n^{2})\) 。时间复杂度是 \(O(n^{2} \log n^{2} 2^{n})\) 的。

得到了左部点子集的大小 \(|\mathbb{S}|\) 后，需要删除的邻居个数是 \(|\mathbb{N(\mathbb{S})|} - |\mathbb{S}| + 1\) ，注意邻居集的大小不能误解成 \(N\) ，因为
\(|\mathbb{N\mathbb{S}}|\) 恒为 \(N\) 当且仅当二分图是完全图。\(|\mathbb{N\mathbb{S}}|\) 在一般图中也不一定比 \(|\mathbb{S}|\) 大。

注意 \(N - |\mathbb{N(\mathbb{S})}|\) 的非邻居点，删除或者不删除都是不影响的 \(S\) 的 \(MC\) 约束的。这时候显然不删除会更好，有些问题中可能全删除会更好。

这个复杂度会超时。对与 \(n=20\) ，\(O(n^{2} 2^{n})\) 就已经是很危险的 \(4 \times 10^{8}\) 了，再带个 \(\log_{2} N^{2}\) 看起来是纯寄的。

思考4：
上面存在一个很严重的逻辑错误。
当我们枚举了一个左部点子集 \(S\) ，删除邻居的方式，显然并非枚举一些 \(x \in \mathbb{S}\) ，通过删除 \(x\) 关联的边，来删除邻居。如果错误的使用了这种方式，邻居集合大小会达到 \(O(n^{2})\) ，显然这是很容易证伪的。

实际上，在确定了 \(\mathbb{S}\) 后，我们要预处理好 \(\mathbb{N \mathbb{S}}\) 中每个元素，被 \(\mathbb{S}\) 中的元素贡献了多少边权。这个预处理是 \(n^{2}\) 的，而实际上的邻居集合大小只有 \(O(n)\) 。这样的话 \(O(n^{2} + n \log n)\) 的瓶颈在于 \(O(n^{2})\) 。所以最终复杂度是 \(O(n^{2} 2^{n})\) 。

但是这个复杂度其实还是比较危险的，1 秒肯定过不去。虽然这个题开了 5 秒。

如果 \(O(2^{n})\) 二进制枚举子集，最后还需要 \(O(n)\) 检查子集里有那些元素，复杂度是 \(O(2^{n} n)\) 。
dfs 可以做到只 \(O(2^{n})\) 枚举，能在过程中检查哪些元素是当前子集的，复杂度是 \(O(2^{n})\) 。
但通常来说不会卡这个复杂度，毕竟 dfs 常数大，很不好对着时间复杂度卡。

画个图吧

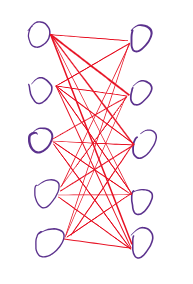
这里是一个 \(\mathbb{K}_{5,5}\) 。

当我们选了左部点的两个点子集 \(\mathbb{S}\)

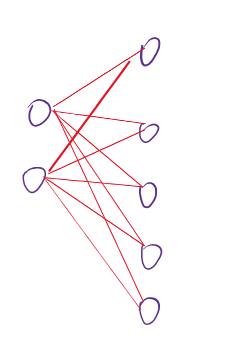
\(\mathbb{S}\) 的邻居集 \(\mathbb{N(\mathbb{S})}\) 大小是 \(5\) 。我们通过遍历 \(\mathbb{S}\) 记录 \(\mathbb{N(\mathbb{S})}\) ，并对 \(\forall x \in \mathbb{N(\mathbb{S})}\) 记录 \(\mathbb{S}\) 过来的边的贡献。

于是我们就得到了这么一个 \(\mathbb{N(\mathbb{S})}\) ，里面有右部点 \(\{1,2,3,4,5\}\) ，并且右部点 \(1\) 记录了左部点 \(1,2\) 过来的贡献，右部点 \(2\) 记录了左部点 \(1,2\) 过来的贡献……右部点 \(5\) 记录了左部点 \(1,2\) 过来的贡献。

当二分图 \(\mathbb{G}=(\mathbb{V},\mathbb{E}) = \mathbb{V}_1,\mathbb{V}_2\) 非完全图时，每个右部点得到的左部点贡献不能认为总是一样的。

实现：

这题的实现还是有点东西的，怎么枚举，怎么算贡献，都有东西的。

在图中确定一个点集，删除这个点集的邻居，这件事情是需要一些手法的。在确定点集后，可以标记哪些点是邻居，并预处理掉他们的邻居的贡献。

view

const int MAXN=25;
int N,tot,c;
i64 ans,res;
i64 a[MAXN][MAXN],wt[MAXN],ns[MAXN];
signed main(){
	cin.tie(nullptr)->ios::sync_with_stdio(false);
	rd(N);
	L(i,1,N)L(j,1,N)rd(a[i][j]);
	int M=bit(N);
	ans=INFL;
	L(mask,1,M-1){
		L(i,1,N)if(mask&bit(i-1)){
			L(j,1,N)if(a[i][j]!=-1){
				wt[j]+=a[i][j];
			}
		}
		tot=0;
		L(j,1,N)if(wt[j])ns[++tot]=wt[j];
		sort(ns+1,ns+tot+1);
		c=__builtin_popcount(mask);
		c=max(0,tot-c+1);
		res=0; L(j,1,c)res+=ns[j];
		chkmin(ans,res);
		L(j,1,N)wt[j]=0;
	}
	wrn(ans);
	return 0;
}

总结：
主要揭示了 MC 定理在二分图上的一些基础应用方式。包括一些基础的图上有关邻居的贡献处理。

2. MC 定理的带权应用

2.1. 洛谷 P11816

给一个 \(A \times B \times C\) 的三维棋盘。对于坐标 \((i,j,k)\) ，初始有 \(a_{i,j,k}\) 个棋子，最终有 \(b_{i,j,k}\) 个棋子。坐标 \((i,j,k)\) 位置上的棋子可以向 \((i+1,j,k),(i,j+1,k),(i,j,k+1)\) 移动。问能否从初始状态移动棋子达到最终状态。

\(1 \leq A \leq 10^{4}\) \(1 \leq B,C \leq 6\) 。

2.2. 洛谷 P9339

有 \(N\) 种物品，每种物品有 \(A_i\) 个，给 \(M\) 个数 \(B_1, B_2, \cdots, B_M\) ，需要将物品分成尽可能少的组，满足

• 每组物品种类两两不同
• 每组物品个数 \(\in \{B\}\)

回答具体如何分组：分多少组，每组的有多少物品且物品是第几种。不可分组则回答 \(-1\) 。

\(1 \leq N,M,\sum A_i \leq 15000\) ，\(1 \leq B_i \leq N\) 。

思考：

也别思考了，直接说结论吧。

第一步： 我们要假设最终选取了 \(K\) 个组，每组大小分别为 \(C_1,C_2, \cdots, C_K\) 。首先显然是要满足 \(\sum_{i=1}^{N} A_i = \sum_{i=1}^{K} C_i\) 的。

接下来考虑，对一开始有的 \(N\) 种物品，每种物品对每个组连一条容量为 \(1\) 的无向边。

3. 洛谷 ARC076F、CF1949B

4. CF1519F

5. 洛谷 P3679

6. CF981F

7. 洛谷 P3488

8. ARC106E

9. ARC080F

开胃菜，并非 MC 定理。