Codeforces Round #613 (Div. 2) （A-E）

A略

 

 

 

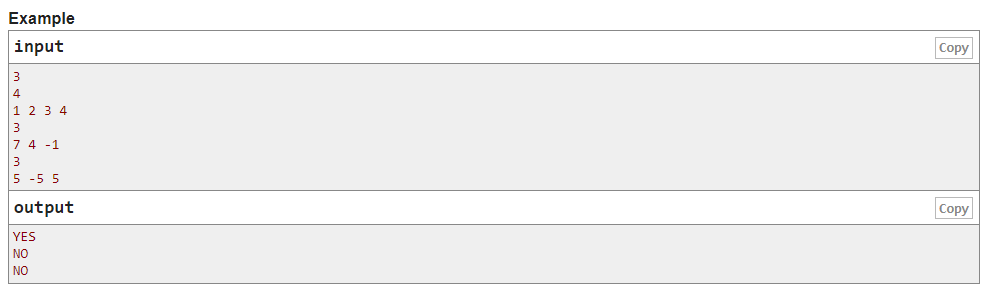
直接求和最大的子序列即可（注意不能全部选中整个子序列）

or

 

 

#include<bits/stdc++.h>

using namespace std;

void solve(){
	int n;
	cin>>n;
	vector<int> a(n);
	vector<long long> sum(n+1,0);	
	for(int i=0;i<n;i++)
		scanf("%d",&a[i]);
	for(int i=1;i<=n;i++)
		sum[i]=sum[i-1]+a[i-1];
	long long mx=-1e18;
	int val=0;
	for(int i=1;i<=n;i++){
		if(i==n&&val==0) continue; 
		mx=max(mx,sum[i]-sum[val]);
		if(sum[i]<=sum[val]) val=i;
	}
	if(mx>=sum[n]) puts("NO");
	else puts("YES");
}

int main(){
	int t;
	cin>>t;
	while(t--)
		solve();
}

　　

 

 

 

 

 设X的素因子分解式为 p1^c1*p2^c2*p3^c3...，且lcm(a,b)=X

 

或者也可以利用二进制来枚举

二进制枚举的方法（来自官方题解）

#include <bits/stdc++.h>
using namespace std;
#define finish(x) return cout << x << endl, 0
#define ll long long

ll x;

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cin >> x;
    vector <ll> f;
    for(ll i = 2 ; i * i <= x ; i++){
        if(x % i == 0){
            ll cur = 1;
            while(x % i == 0){
                x /= i;
                cur *= i;
            }
            f.push_back(cur);
        }
    }
    if(x > 1) f.push_back(x);
    int n = f.size();
    ll ansa = 1e18, ansb = 1e18;
    for(int i = 0 ; i < (1 << n) ; i++){
        ll a = 1, b = 1;
        for(int j = 0 ; j < n ; j++){
            if((i >> j) & 1) a *= f[j];
            else b *= f[j];
        }
        if(max(a, b) < max(ansa, ansb)){
            ansa = a;
            ansb = b;
        }
    }
    cout << ansa << " " << ansb << endl;
}

　枚举因子

#include<bits/stdc++.h>

using namespace std;

int main(){
	long long x;
	cin>>x;
	long long ans=1;
	for(long long i=2;i*i<=x;i++){
		if(x%i==0){
			if(__gcd(i,x/i)==1) {
				ans=i;
			}
		}
	} 
	cout<<ans<<' '<<x/ans<<endl;
}

　　

 

 不难想，主要是代码写法，做法参考官方题解

 

 

#include<bits/stdc++.h>

using namespace std;

const int maxn=1e5+5;

int solve(vector<int>& c,int dep){
	if(c.size()==0||dep<0) return 0;
	vector<int> l,r;
	for(auto i:c){
		if(((i>>dep)&1)==0) l.push_back(i);
		else r.push_back(i);
	}
	if(l.size()==0) return solve(r,dep-1);
	if(r.size()==0) return solve(l,dep-1);
	return min(solve(l,dep-1),solve(r,dep-1))+(1<<dep);
}

int main(){
	int n;
	cin>>n;
	vector<int> a(n);
	for(int i=0;i<n;i++)
		scanf("%d",&a[i]);
	cout<<solve(a,30);
	
}
 

　　

 

 

 

 

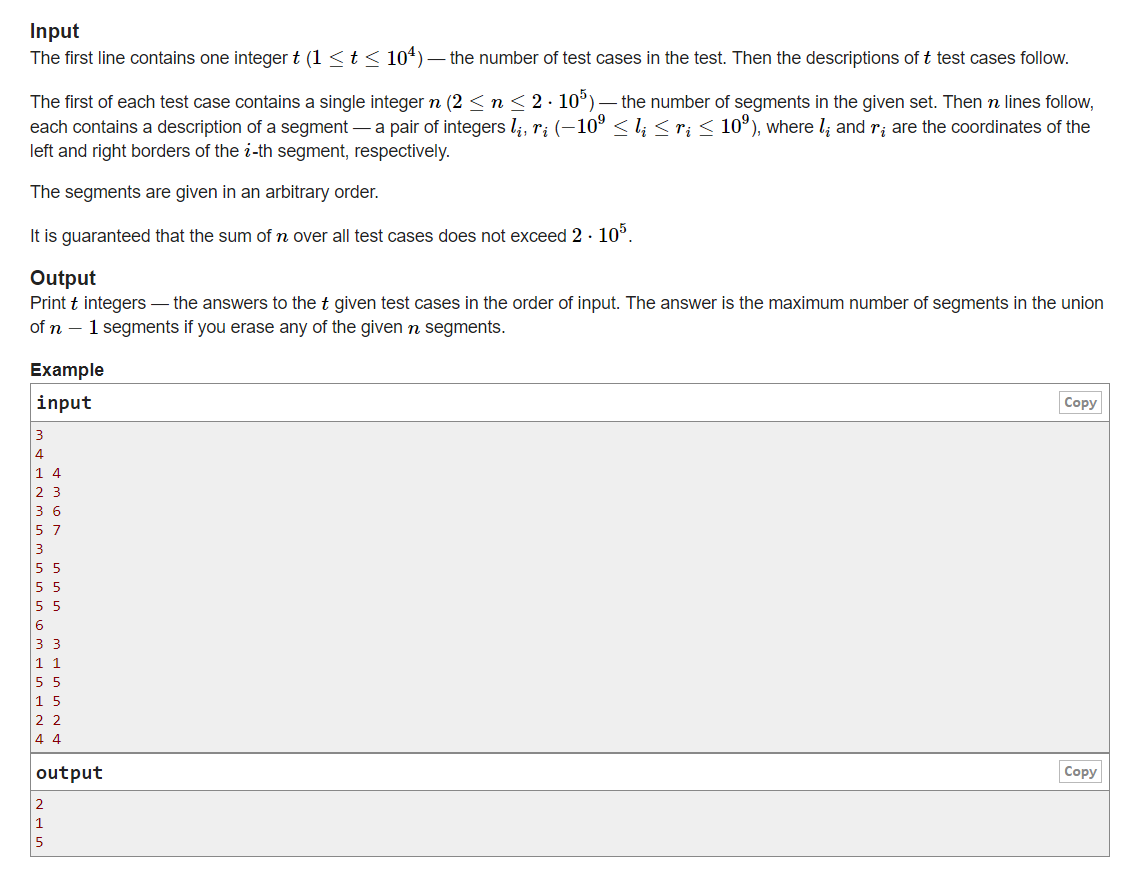
 首先是由计数不同区间改为计数区间的左端点个数

然后利用扫描线算法将原始区间排序，然后开始遍历

 

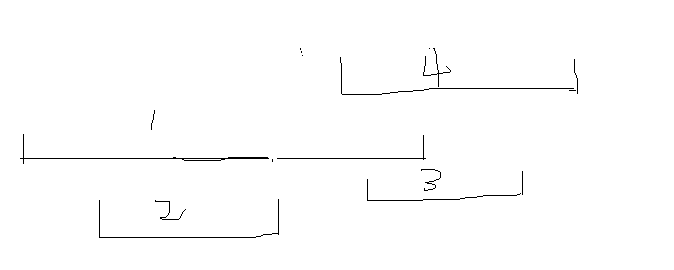
 我们首先枚举到的是1的左端点，我们存下他（用set就好），然后到达2的左端点，此时发现2被一个区间覆盖，就是被区间1，因此删除掉区间1会导致增加一个新的左端点，也就是区间2的左端点，

因此我们让ans[1]++，然后将区间2加进set，之后2的右端点，set删除2，又到了4的左端点，发现删除区间又会导致增加一个新的左端点，因此ans[1]++,之后将区间4加进set,

然后到达区间3的左端点，此时set中有两个，也就是说我们不管删除set中的哪一个都不会导致增加新的左端点，所以ans不变,将3加进去即可

这样做只是计算了删除掉这个区间之后增加了多少新的左端点，因此还需要计算删除掉这个区间之后会不会导致失去左端点，这个就很简单了，不废话了

#include<bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)
#define fore(i, s, t) for (int i = s; i < (int)t; i++)
#define fi first
#define se second

using namespace std;

const int maxn=2e5+5;

typedef pair<int,int> pi;

const int inf=2e9;

map<int,int> ls;

int get(vector<pi> a){
	int cnt=0;
	int l=-inf,r=-inf;
	sort(a.begin(),a.end());
	for(int i=0;i<a.size();i++){
		if(a[i].fi>r) {
			if(r!=-inf) ls[l]=0;
			++cnt;
			l=a[i].fi,r=a[i].se;
		}
		else r=max(r,a[i].se);
	}
	ls[l]=0;
	return cnt;
}

void process(vector<pair<int,pi>>& qr,vector<int>& ans){
	set<int> now;
	forn(i,qr.size()){
		vector<int> tl,tr;
		int j=i-1;
		while(j+1<qr.size()&&qr[j+1].fi==qr[i].fi){
			j++;
			if(qr[j].se.fi==1)  tl.push_back(qr[j].se.se);
			else tr.push_back(qr[j].se.se);
		}
		if(now.size()==1&&tl.size()) ++ans[*now.begin()];
		for(int it:tl) now.insert(it);
		for(int it:tr) now.erase(it);
		i=j;
	}
}

void solve(){
	int n;
	cin>>n;
	vector<pi> a(n);
	for(int i=0;i<n;i++){
		scanf("%d%d",&a[i].fi,&a[i].se);
	}
	vector<pair<int,pi>>qr;
	for(int i=0;i<n;i++){
		qr.push_back({a[i].fi,{1,i}});
		qr.push_back({a[i].se,{-1,i}});
	}
	sort(qr.begin(),qr.end());
	ls.clear();               
	int cur=get(a);
	vector<int> ans(n,0);
	process(qr,ans);
	forn(i,n) if(ls.count(a[i].fi)) ++ls[a[i].fi];
	forn(i,n) if(ls[a[i].fi]==1) --ans[i];
	printf("%d\n",*max_element(ans.begin(),ans.end())+cur);
}
int main(){
	int n;
	cin>>n;
	forn(i,n) solve();
}