Math(whk)

# 成达爷/kk Orz Liujiahua

# 函数

## Genshin

对于一个圆心为原点半径为 $r$ 的圆，考虑上面的点 $(x,y)$ ，显然勾股定理 $x^2+y^2=r^2$，这就是圆的解析式。

考虑圆心为 $(a,b)$ 的点，把它平移到原点，即平移到原点距离为 $(-a,-b)$，那么解析式为 $(x-a)^2+(y-b)^2=r^2$，于是就可以联立了，假设与 $y=x-k$ 联立，那么把这个一次函数带入圆的 $y$ 上即可，发现联立之后的是一个二次函数，其解就是两个交点的 $x$ 坐标，如果求切线的话，那么让 $\Delta=0$ 即可。

## 椭圆

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=r^2$

## 三角函数

弧度制：$\pi=180 \degree$，简单来说就是把圆心角表示的度数表示为单位圆上的弧长。

扩展角的定义，把一个角理解成 $x$ 轴绕原点旋转的角度，顺时针转动，角就是负的。

### [正弦余弦定理](https://www.bilibili.com/video/BV1a8411A7nM/)。

~~正弦定理ASA AAS解三角形 余弦定理SAS SSS解三角形~~

**正弦定理。**

对于一个三角形 $\triangle ABC$，$\angle A$ 对边 $a$，$\angle B$ 对边 $b$，$\angle C$ 对边 $c$，那么 $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2r$，其中 $r$ 为三角形外接圆半径。证明的话，从任意一点做直径，直径产生直角与同弧导角，然后就没了。

**余弦定理。**

作出单位圆半径为 $1$，在圆上取一个点 $A$，做它关于 $x$ 轴的垂线，交于 $B$，连上 $OA$，这便是一个直角三角形。


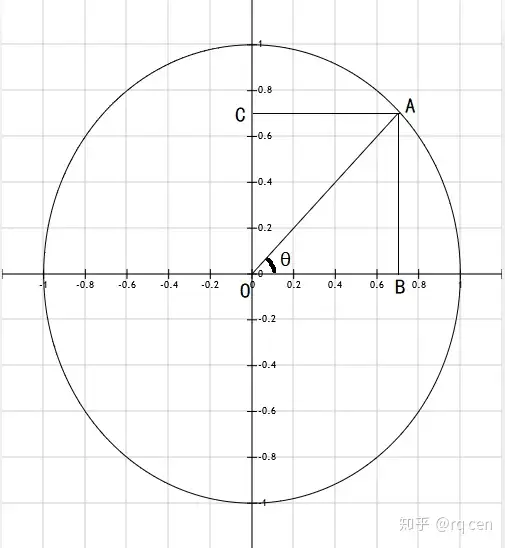
发现 $\sin \theta= \frac{AB}{OA}=AB$ ，$\cos \theta= \frac{OB}{OA}=OB$ ，所以 $A(\cos \theta,\sin \theta)$
。这样，三角函数变成了一个单位圆上的坐标，就可以扩展到实数域了。根据这个，显然可知 $\cos(-x)=\cos(x),\sin(-x)=-\sin(x)$

### [和差](https://www.bilibili.com/video/BV1MU4y1K7cZ/)：


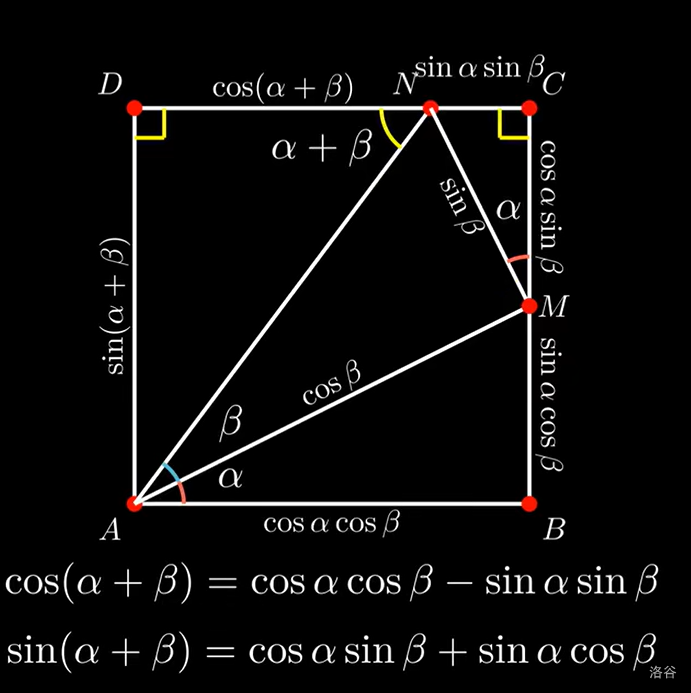
好推。根据 $\sin(x)^2+\cos(x)^2=1$，二倍角公式就出来了。

差化积：

$$ \sin(a)=\sin(\frac{a+b}{2}+\frac{a-b}{2}) \\
=\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})+\cos(\frac{a-b}{2})\sin(\frac{a+b}{2})\\
\\
\sin(b)=\sin(\frac{a+b}{2}+\frac{b-a}{2}) \\
=\cos(\frac{a+b}{2})\sin(\frac{b-a}{2})+\cos(\frac{b-a}{2})\sin(\frac{a+b}{2})\\
=-\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})+\cos(\frac{a-b}{2})\sin(\frac{a+b}{2})\\
\\
\sin(a)-\sin(b)=2\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})
$$

# 拉差

把一车点 $(x_{1\dots n},y_{1\dots n})$ 找到一个多项式来描述。

$p_i(x)=\prod_{j\leq n,j\neq x} \frac{x-x_j}{x_i-x_j}$

$L_i(x)=\sum_{i=1}^{n} y_i\times p_i(x)$

证不了一点

### 因式定理

对于多项式 $f(x)$，如果 $(x-a)$ 为 $f(x)$ 的因数，那么 $f(a)=0$。

# 导数

[再%一遍](https://www.luogu.com.cn/blog/jasonliujiahua/dao-shuo-ji-qi-ying-yong)

对于函数 $f(x)$，根据导数的定义，它的一阶导数是 $f'(x)=\displaystyle \lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$。

通俗理解导数的阶是对着这个函数导了几次，对一个函数的一阶导数导就为二阶导数，导数可以类比为差分。$\lim$ 为趋近于某个值时式子的值的趋近

### $f(x)=x^a,f(x)'=ax^{a-1}$
因为 $\Delta$ 趋近于无穷小，所以我们不考虑 $\Delta$ 的次数大于 $1$ 的情况，二项式定理套公式即可，如果带系数直接乘上系数即可。

### $f(x)=\sin x,f(x)'=\cos x$


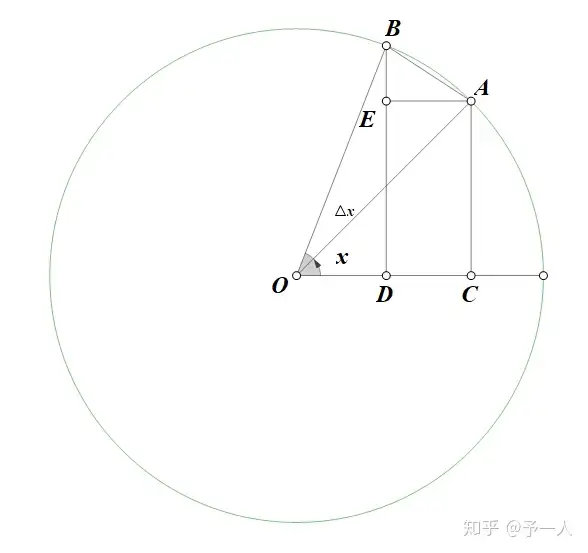
相当强的直观证明。导角导出 $\angle OBA=x+\frac{\Delta}{2}$，而导数公式里的分子为 $BE$，$\Delta x$ 用弧度制就是弧 $AB$ 的长，趋近于 $AB$ 的长。那么 $\frac{BE}{AB}=\cos x$。

性质：$[f(x)+g(x)]'=f'(x)+g'(x)$，拆开柿子即可。

## [泰勒展开](https://www.bilibili.com/video/BV1Gx411Y7cz)

用一个多项式函数近似描述一个函数在某个点附近的图像。

即在该点时，我们要尽可能地让多项式函数的高阶导数等于原函数。在一个多项式中，根据 $f(x)=ax^n,f'(x)=anx^{n-1}$ 与可加性即可。对于多项式，他的导数导一次相当于降了一次幂。

举个例子，对函数 $f(x)=ax^3+bx^2+cx+d$ 来近似 $g(x)=\cos(x)$，在 $x=0$ 处，将 $x=0$ 带入，$cos(0)=1,d=1$。

一阶导数为 $f(x)'=3ax^2+2bx+c,g(x)=-\sin(x)$，将 $x=0$ 带入，$\sin(0)=0,c=0$。

二阶导数为 $f(x)''=2\times 3ax+2b,g(x)=-\cos(x)$，将 $x=0$ 带入，$-\cos(0)=-1,2b=-1,b=-\frac{1}{2}$。

三阶导数为 $f(x)'''=2\times 3a,g(x)=\sin(x)$，将 $x=0$ 带入，$sin(0)=0,6a=0,a=0$。

我们得到的近似多项式为 $y=-\frac{1}{2}x^{2}+1$，画下图发现和 $cos(x)$ 在 $x=0$ 附近比较像。

那么，我们把这个扩展到无线