CS:APP第二章笔记
2 信息的表示和处理
2.1 信息存储
- 最小可寻址的内存单位——字节(byte)
- 内存中的每个字节都由唯一的数字标识,成为地址(address),所有可能地址的集合就称为虚拟内存空间(virtual address space)
- 程序对象(program object):程序数据、指令和控制信息
2.1.2 字数据大小
- 字长:指明指针数据的标称大小(normal size)。
- 对于字长为\(\omega\)位的机器而言,虚拟地址空间最大大小为\(2^\omega\),虚拟地址的范围为\(1\backsim2^\omega -1\)
2.1.3 寻址和字节顺序
- 最低有效字节在最前面的方法称为小端法,反之为大端法,例如0x01234567

2.1.4 表示代码
- 不同的机器类型使用不同的且不兼容的指令和编码方式。
2.1.9 移位运算
- 参数x经过不同移位运算后的结果
| 操作 | 值 |
|---|---|
| 参数x | [01100011] [10010101] |
| x << 4 | [00110000] [01010000] |
| x >> 4(逻辑右移) | [00000110] [00001001] |
| x >> 4(算术右移) | [00000110] [11111001] |
注意:C语言标准并没有明确定义对于有符号数应该使用哪种类型的右移——算术右移或者逻辑右移都可以。但事实上,几乎所有的编译器/机器组合都对有符号数使用算术右移。
2.2 整数表示
- 符号术语
| 符号 | 类型 | 含义 |
|---|---|---|
| B、T、U | 数值类型 | 二进制、补码、无符号数 |
| \(x2y_\omega\)(\(x,y\in\{B,T,U\}\)) | 函数 | x类型转y类型 |
| \(xMin_\omega\)(\(x\in \{B,T,U\}\)) | 常数 | x类型最小值 |
| \(xMax_\omega\)(\(x\in \{B,T,U\}\)) | 常数 | x类型最大值 |
| \(+^x_\omega\)/\(*_\omega^x\)(\(x\in \{t,u\}\)) | 操作 | x类型乘法、加法 |
| \(-^x_\omega\)(\(x\in \{t,u\}\)) | 操作 | x类型取反 |
| \(\omega\) | 常数 | 表示数据位数 |
2.2.1 整型数据类型
- C语言标准定义了每种数据类型必须能够表示的最小取值范围。(如果希望代码具有最大的可移植性,只得使用以下范围)(C标准并未要求整数以补码表示)
| C数据类型 | 最小值 | 最大值 |
|---|---|---|
| char | -127 | 127 |
| unsigned char | 0 | 255 |
| short | -32767 | 32767 |
| unsigned short | 0 | 65535 |
| int | -32767 | 32767 |
| unsigned | 0 | 65535 |
| long | -2147483647 | 2147483647 |
| unsigned long | 0 | 4294967295 |
| int32_t | -2147483647 | 2147483647 |
| uint32_t | 0 | 4294967295 |
| int64_t | -9223372036854775808 | 922372036854775807 |
| uint64_t | 0 | 18446774073709551615 |
2.2.2 无符号数的编码
- 对向量\(\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]\),
\[B2U_\omega(\vec{x})=\sum^{\omega-1}_{i=0}x_i2^i
\]
- 无符号数编码表示的范围:\(0\backsim2^\omega-1\)
- 函数\(B2U_\omega\)是一个双射。无符号数的编码具有唯一性。
2.2.3 补码编码
- 对向量\(\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]\),
\[B2T_\omega(\vec{x})=-x_{\omega-1}2^{\omega-1}+\sum^{\omega-2}_{i=0}x_i2^i
\]
- 补码表示范围:\(-2^{\omega-1}\backsim2^{\omega-1}-1\)
- 函数\(B2T_\omega\)是一个双射。补码编码具有唯一性。
- \(|TMin_\omega|=|TMax_\omega|+1\)
2.2.4 有符号数和无符号数之间的转换
- 在C语言中,有符号数和无符号数直接的转换一般保持位值不变。即对\(TMin_\omega\le x\le TMax_\omega\),有
\[T2U(x)=\begin{cases}x+2^\omega,\space\space\space x < 0 \\ x,\space\space\space\space\space\space\space\space\space\space\space\space x \ge 0 \end{cases}
\]
2.2.5 C语言中的有符号数和无符号数
- 隐式转换
- 有(无)符号数给无(有)符号数赋值:有(无)符号数转换位无(有)符号数
- 一个运算的两个运算数一个有符号一个无符号,自动转换为无符号,如
-1<0U为假
2.2.6 拓展一个数字的位表示
- 无符号数拓展:在高位添加0
- 补码的拓展:
- 原理:宽度位\(\omega\)的向量\(\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]\),和宽度为\(\omega'\)的向量\(\vec{x}'=[x_{\omega-1},x_{\omega-1},...,x_{\omega-1},x_{\omega-2},...,x_0]\),其中\(\omega<\omega'\),则\(B2T_\omega(\vec{x})=B2T_\omega(\vec{x}')\)
- 方式:在高位添加符号位的值
2.2.7 截断数字
- 无符号数的截断:截断前为\(x\),截断后为\(x'\),则\(x'=x \mod 2^k\)
- 补码的截断:截断后将最高位转换为符号位
2.3 整数运算
2.3.1 无符号加法
- 无符号加法
\[x+^u_\omega y=
\begin{cases}
x+y,\space\space\space\space\space\space\space\space\space\space\space\space\space \space x+y<2^\omega \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space正常\\
x+y-2^\omega,\space\space\space\space\space2^\omega\le x+y<2^\omega\space\space\space\space\space\space\space\space溢出
\end{cases}
\]
- 溢出检测:当且仅当\(x+^u_\omega y<x(或y)\)时溢出
- 无符号取反
\[-^u_\omega x =
\begin{cases}
x,\space\space\space\space\space x = 0 \\
2^\omega-x,x>0
\end{cases}
\]
2.3.2 补码加法
- 补码加法
\[x+^t_\omega y=
\begin{cases}
x+y-2^\omega, 2^{\omega-1}\le x+y\space\space\space\space\space\space\space\space\space\space\space 正溢出\\
x+y,-2^{\omega-1}\le x+y < 2^{\omega-1}\space\space\space\space正常\\
x+y+2^\omega,x+y<-2^{\omega-1}\space\space\space\space\space\space\space\space负溢出
\end{cases}
\]
- 溢出检测:\(s=x+^t_\omega y\)当且仅当\(x>0,y>0,s\le0\)时发生了正溢出,\(x<0,y<0,s\ge 0\)时发生了负溢出
2.3.3 补码的非
- 补码的非
\[-^t_\omega x=
\begin{cases}
TMin_\omega, \space\space\space\space x = Tmin_\omega\\
-x,\space\space\space\space\space\space\space\space\space\space\space x>Tmin_\omega
\end{cases}
\]
- 补码非的位级表示:对\(x\)求非,先对\(x\)每一位求补,再加一,即\(-x=^\backsim x+1\)
2.3.4 无符号乘法
- 无符号乘法(通过截断实现)
\[x*^u_\omega y = (x*y)\mod{2^\omega}
\]
2.3.5 补码乘法
- 补码乘法
\[x*^u_\omega y = U2T_\omega((x*y)\mod{2^\omega})
\]
- 溢出检验:\(p = x*^u_\omega y\),当且仅当\(x\ne 0\)且\(p/x\ne y\)时发生溢出
2.3.6 乘以常数
- 背景:在以往大多数机器上,整数乘法指令相当慢,所以编译器采用移位和加法的组合来代替乘以常数的乘法
- 乘以2的幂\(2^k\),\(x*2^k\)转化为\(x<<k\)
- 乘以任意常数\(k\)时
- 将\(k\)转换为\(2^{k1}+2^{k2}+...2^{kn}\)的形式
- 进而将乘法转化为\((x<<k1)+(x<<k2)+...(x<<kn)\)
- 更进一步将形如\((x<<n)+(x<<(n-1))+..+(x<<(m+1))+(x<<m)\)简化为\((x<<(n+1))-(x<<m)\)
2.3.7 除以2的幂
- \(\lceil x/2^k \rceil = (x+(1<<k)-1)>>k\)
2.4 浮点数
2.4.2 IEEE浮点表示
- IEEE浮点标准用\(V = (-1)^s*M*2^E\)的形式表示一个数:
- 符号\(s\):\(s\)为0时浮点数为正,为1时浮点数为负
- 尾数\(M\):一个二进制小数,范围是\(1\backsim 2-\epsilon\)或\(0\backsim 1-\epsilon\)
- 阶码\(E\):作用是对浮点数加权,权重是\(2^E\),\(E\)可以为负数
- 浮点数的位表示划分为三个字段,分别对这些值进行编码:
- 一个单独的符号位直接编码\(s\)
- \(k\)位的阶码字段
exp=\(e_{k-1}...e_1e_0\)编码阶码\(E\)(float:\(k=8\),double:\(k=11\)) - \(n\)位小数字段
frac=\(f_{n-1}..f_1f_0\)编码尾数\(M\),但编码的值也依赖于阶码字段是否等于0(float:\(n=23\),double:\(n = 52\))
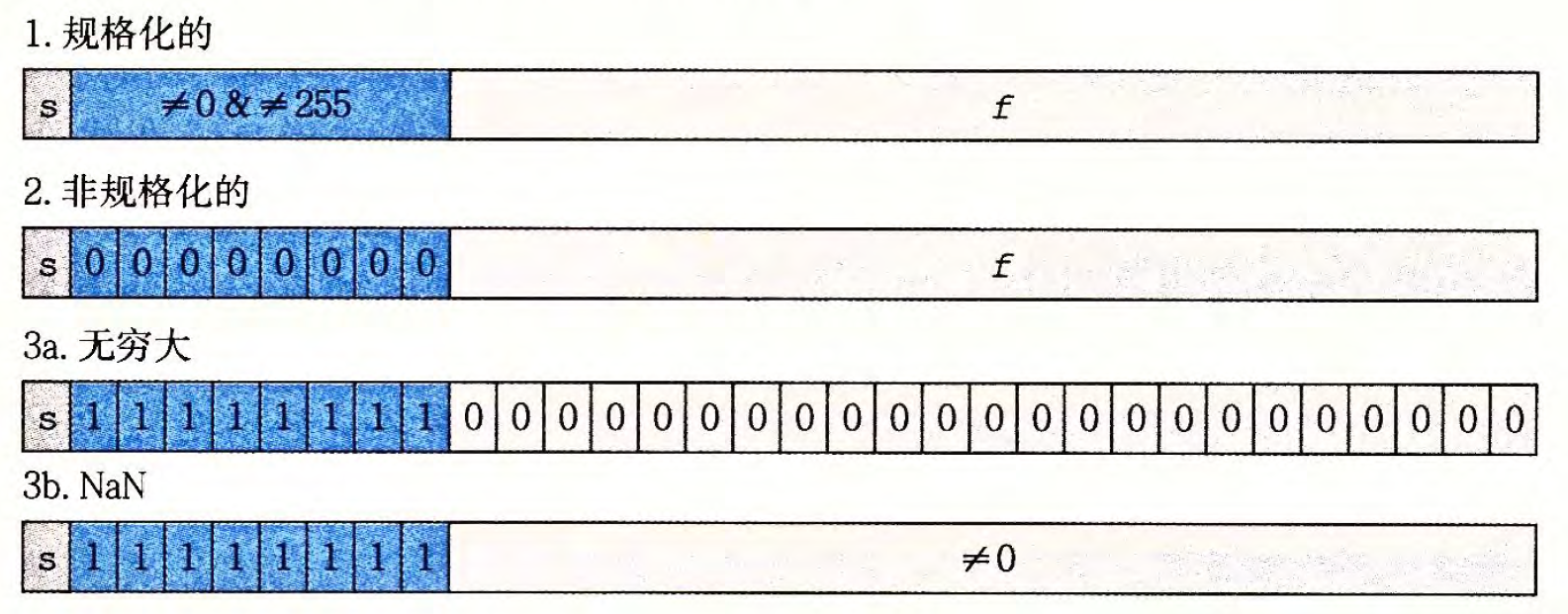
- 浮点数值的分类:
![浮点数值的分类.png]()
- 规格化的值
- exp:exp位模式既不全为0,也不全为1,此时阶码的值为\(E=e-Bias\),\(e\)是表示为\(e_{k-1}..e_1e_0\)的无符号数,\(Bias=2^k-1\),所以对单精度\(E\)的范围是\(-126\backsim127\),对双精度是\(-1022\backsim1023\)
- frac:frac用于描述小数值\(f(0\le f < 1)\),其二进制表示为\(0.f_{n-1}...f_1f_0\)。尾数\(M=1+f\),即包含一个隐含的开头0
- 非规格化的值
- exp位模式全为0,此时阶码的值是\(E=1-Bias\),尾数\(M=f\),即此时不含隐式的0
- 用途一:用于表示\(0\)。如\(+0.0\)可以表示为全0
- 用途二:表示接近0的数
- 无穷大
- 阶码全为1,小数域全为0时表示无穷,\(s\)为0时是正无穷,\(s\)为1时是负无穷
- 用途:表示溢出的结果
- NaN
- NaN是"Not a Number"的缩写
- 用途:用于表示不是实数或无穷的计算计算结果,某些时候也用于表示未初始化的数据
2.4.3 数字示例
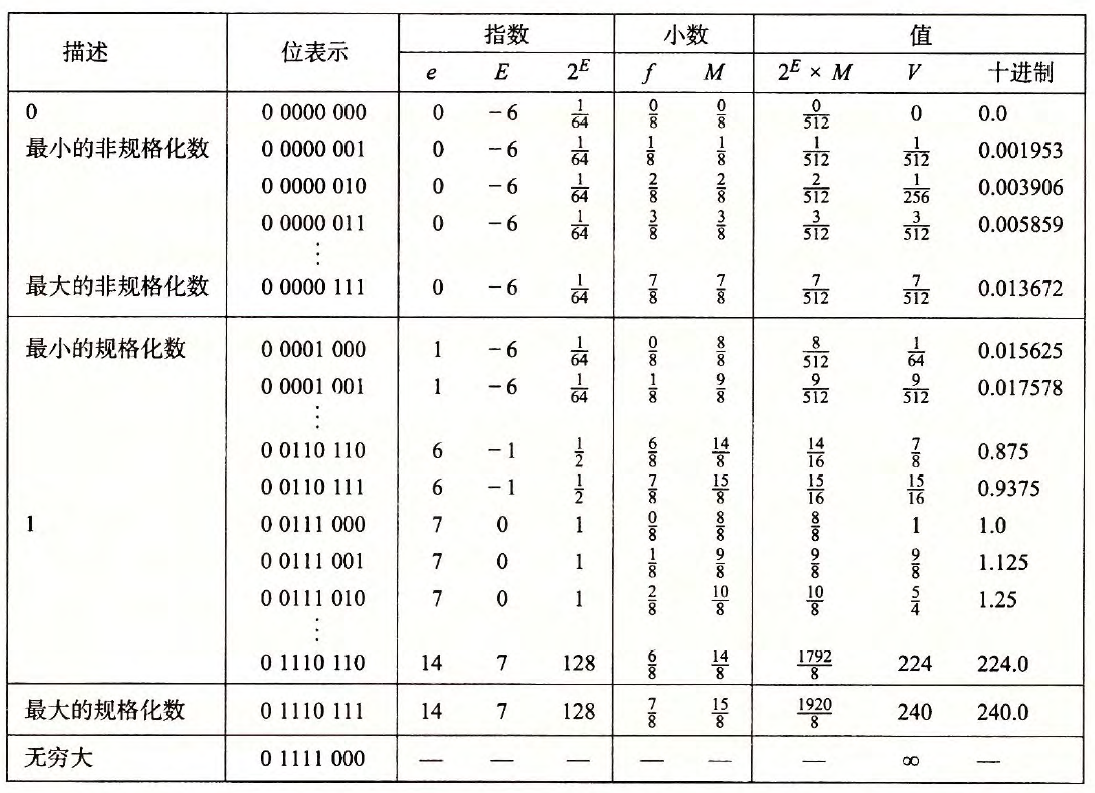
- 性质:比较浮点数的大小可以等价于比较对应无符号数大小
- 特点:
- 值+0.0表示为\(00..00\)
- 最小的正非规格化值表示为\(0\space0..00 \space 0..01\),值为\(2^{-n+2-2^{k-1}}\)
- 最大的正非规格化值表示为\(0 \space 0..00\space1..11\),值为\((1-2^n)*2^{2-2^{k-1}}\)
- 最小的正规格化值表示为\(0\space0..01\space0..00\),值为\(2^{2-2^{k-1}}\)
- 最大的正规格化值表示为\(0\space 1..10\space 1..11\),值为\((2-2^{-n})*2^{2^{k-1}-1}\)
- 单精度双精度表示示例

2.4.4 舍入
- 目的:匹配近似的浮点形式
- 向偶数舍入(向最接近值舍入)
- 当形如\(xx.xxxxk1_{(2)}\)时(\(k\)为需要保留的最低有效位),舍入需让\(k\)为0的方向舍入
- 当形如\(xx.xxxxk0_{(2)}\)时(\(k\)为需要保留的最低有效位),舍入为\(xx.xxxxk\)
2.4.5 浮点运算
- 性质:
- 除无穷和NaN外所有的浮点数\(x\),满足\(x+^f-x=0\)(\(+\infty +^f-\infty = NaN\))
- 对于任意\(x\),都有\(NaN+^fx=NaN\)
- 浮点加法具有单调性:如果\(a \ge b\),则对\(x\)不为NaN时,\(x+a\ge x+b\)(无符号和补码均不具备该性质)
- 对任意不为NaN的浮点数,\(c\ge0,a\ge b\)则\(a*^fc\ge b*^fc\)
- 对任意不为NaN的浮点数\(a\),均有\(a*^fa\ge0\)
- 浮点数运算具有交换律
- 浮点数不具有结合律,比如在单精度时,因为舍入,
(3.14+1e10)-1e10值为0,3.14+(1e10-1e10)为3.14 - 浮点数乘法不具有分配律,如单精度时
1e20*(1e20-1e20)为0,1e20*1e20-1e20*1e20为NaN
2.4.6 C语言中的浮点数
- C标准不要求机器使用IEEE浮点,编码方式可能会有不同
- 强制类型转换:
- int\(\to\)float:数字不会溢出,但可能舍入
- int或float\(\to\)double:能保留精确的数值
- double\(\to\)float:可能溢出为无穷,也可能被舍入
- float或double\(\to\)int:值向零舍入(如1.99舍入为1,-2.99舍入为2)。也有可能溢出,但C语言没有对这种情况指定固定的结果。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号