树的创建和遍历
链表的创建和遍历(以单链表为例)
创建
1. 尾插法
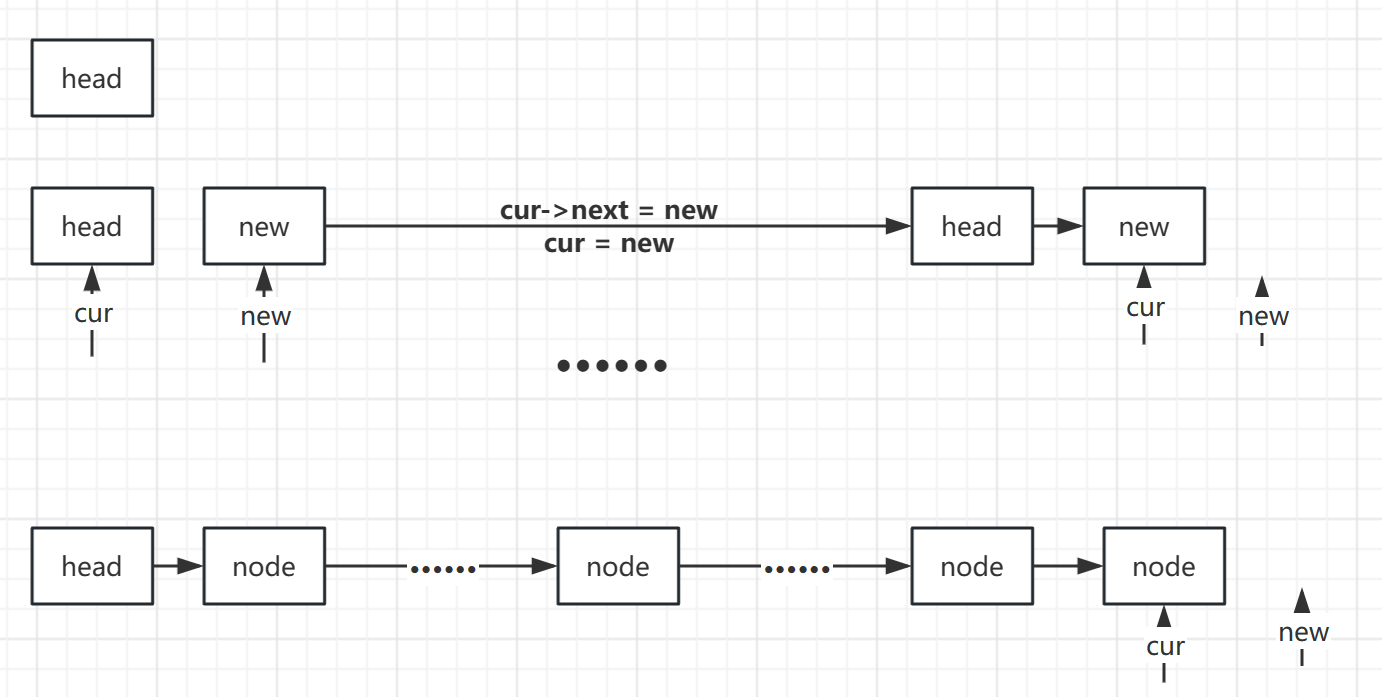
C++实现
struct ListNode{
int val;
// 这里不赋初值,则在建立链表时就要置空,否则链表末尾指针不为空
ListNode* next = nullptr;
};
// 根据传入的数组构建链表
ListNode* buildList(const vector<int> &arr){
if(arr.empty()){
return nullptr;
}
ListNode* head = new ListNode;
head->val = arr[0];
ListNode* pre = head;
for(int i = 1; i < arr.size(); ++i){
ListNode* cur = new ListNode;
cur->val = arr[i];
pre->next = cur;
pre = cur;
}
return head;
}
2. 头插法
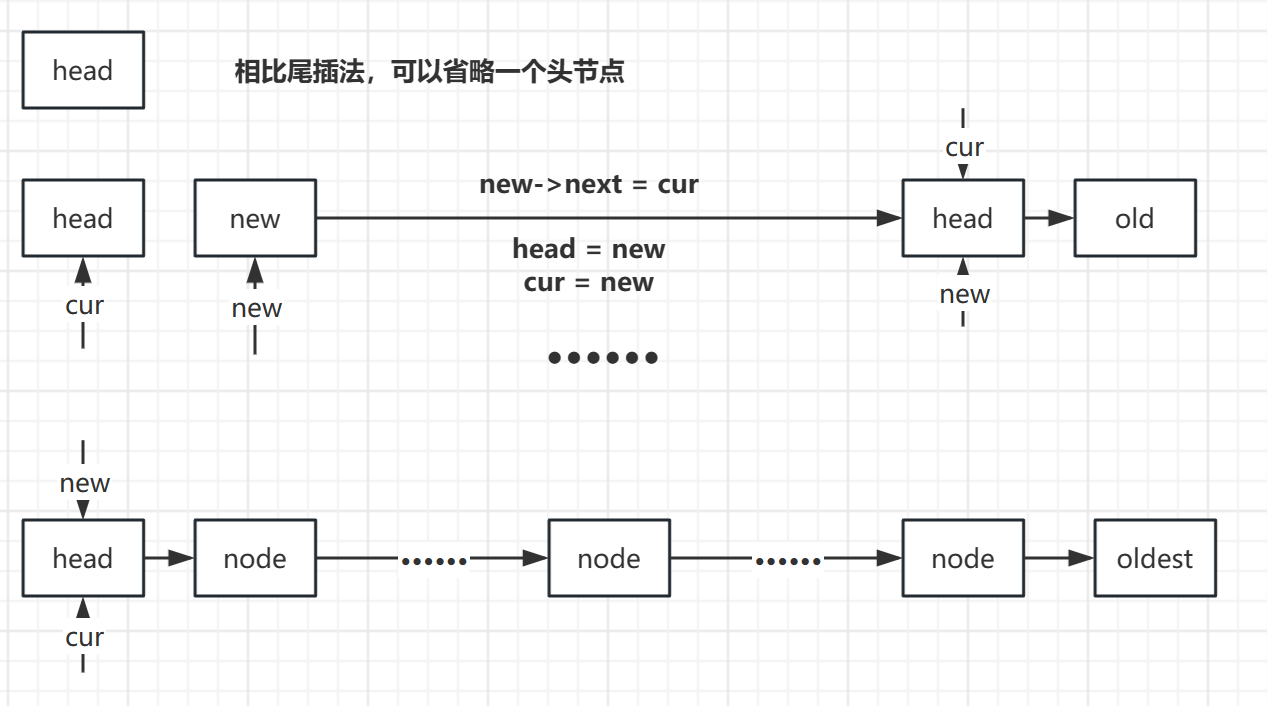
C++实现
struct ListNode{
int val;
// 这里不赋初值,则在建立链表时就要置空,否则链表末尾指针不为空
ListNode* next = nullptr;
};
// 根据传入的数组构建链表
ListNode* buildList(const vector<int> &arr){
if(arr.empty()){
return nullptr;
}
ListNode* head = new ListNode;
head->val = arr[0];
ListNode* pre = head;
for(int i = 1; i < arr.size(); ++i){
ListNode* cur = new ListNode;
cur->val = arr[i];
pre->next = cur;
pre = cur;
}
return head;
}
遍历
C++实现
void travelList(ListNode* head){
while(head != nullptr){
cout<<head->val<<" ";
head = head->next;
}
cout<<endl;
}
二叉树的创建和遍历
创建
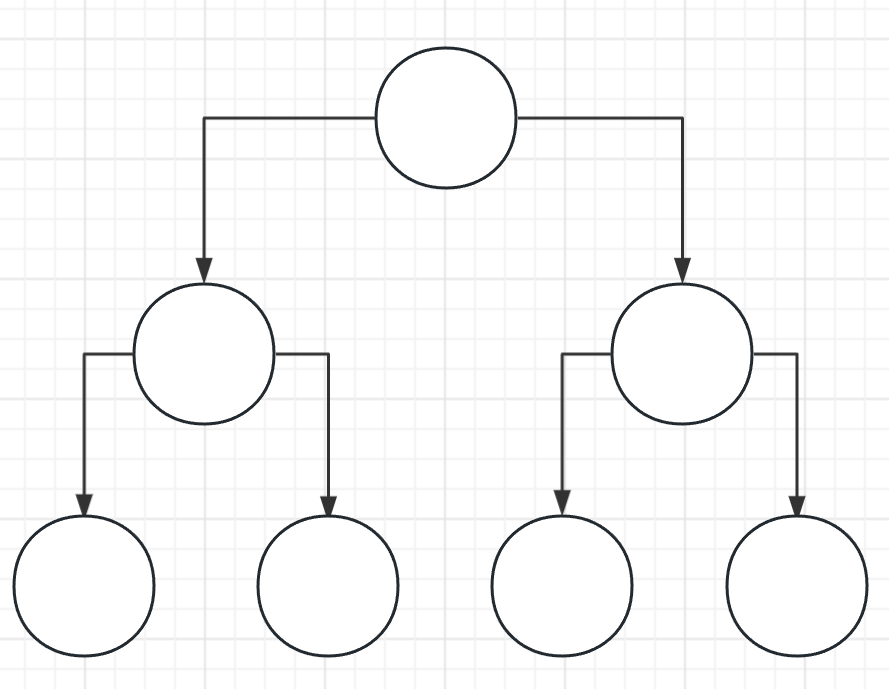
顺序存储
适用于满二叉树或完全二叉树:
- 满二叉树
![image]()
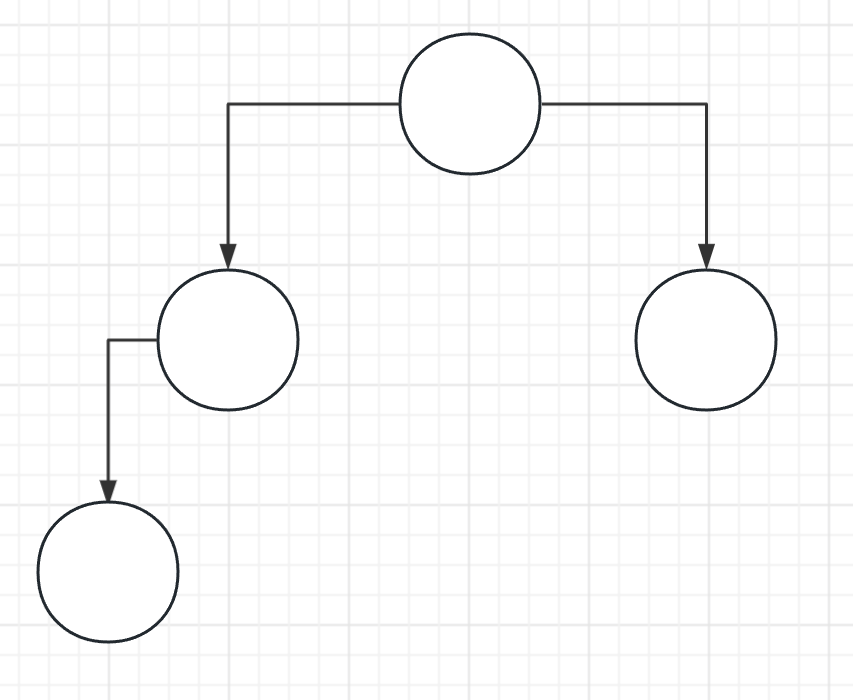
- 完全二叉树
![image]()
按层序用数组存储数据即可,利用下标之间的关系,表明节点间的父子关系。
链式存储
C++实现
struct TreeNode{
int val;
TreeNode* left = nullptr;
TreeNode* right = nullptr;
};
TreeNode* bulidTree(){
// 输入-1时,表示空节点
int value;
cin>>value;
if(value == -1){
return nullptr;
}
TreeNode* node = new TreeNode;
node->val = value;
node->left = bulidTree();
node->right = bulidTree();
return node;
}
遍历
C++实现
void travelTree(TreeNode* node){
if(node == nullptr){
return ;
}
cout<<node->val<<" ";
travelTree(node->left);
travelTree(node->right);
}
多叉树的创建和遍历
创建
链式存储
输入建立多叉树,输入的格式是每个节点的值和子节点数目:
1 3
2 2
5 0
6 0
3 0
4 1
7 0
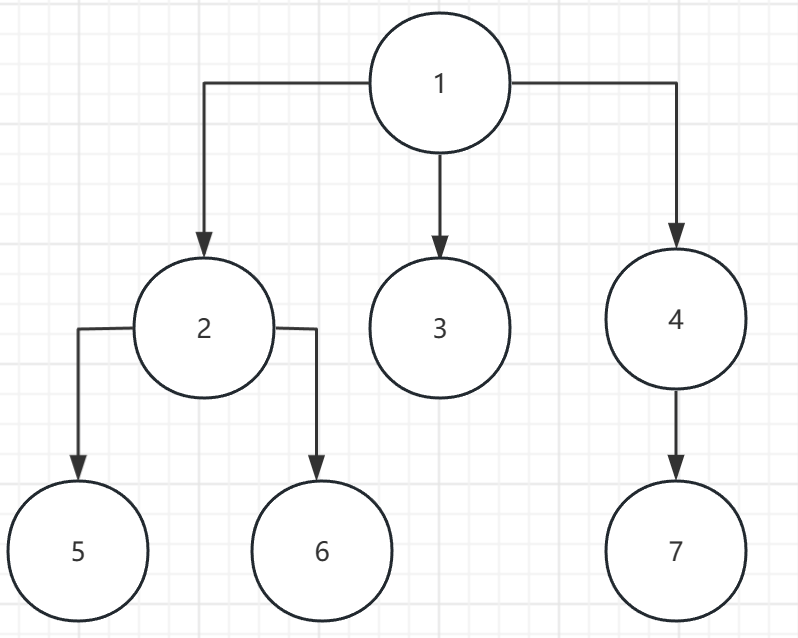
C++实现
struct multiTreeNode{
int val;
vector<multiTreeNode*> children;
};
multiTreeNode* bulidMultiTree(){
int value;
int n;
cin>>value>>n;
multiTreeNode* node = new multiTreeNode;
node->val = value;
for(int i = 0; i < n; ++i){
node->children.emplace_back(bulidMultiTree());
}
return node;
}
遍历
C++实现
void travelMultiTree(multiTreeNode* node){
if(node == nullptr){
return ;
}
cout<<node->val<<" ";
for(auto i : node->children){
travelMultiTree(i);
}
}
总结
以上操作都是在明确根节点的情况下进行的,但题目经常只给出节点之间的关系,不会明确给出根节点。
此时,就需要使用邻接表来存储树,因为这时就是将树当作图来处理了。
这时只要随意选择一个点当根节点就可以了,毕竟可以是多叉树。
邻接表存储树
多叉树: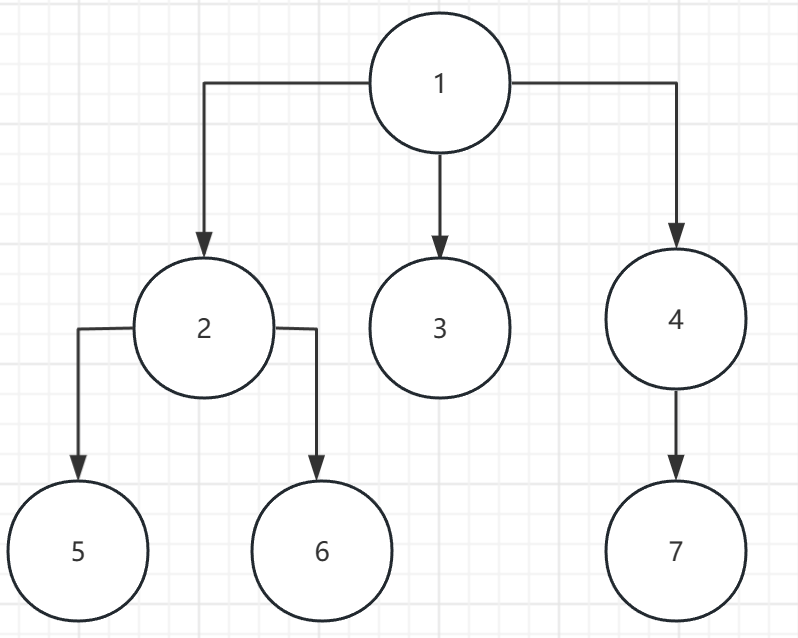
邻接表: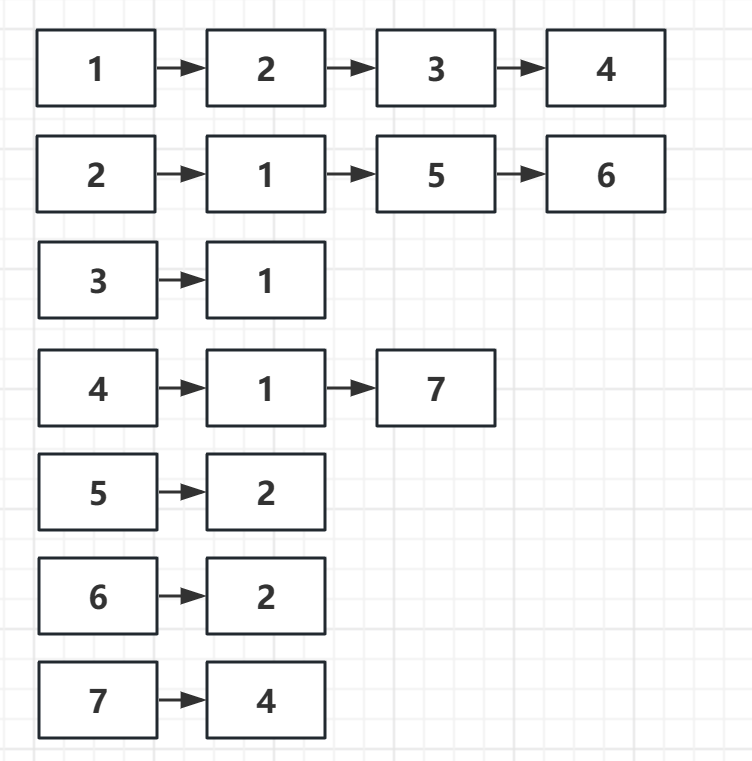
输入:
7
1 2
1 3
1 4
2 5
2 6
4 7
C++代码实现
vector<vector<int>> buildTable(){
int n;
cin>>n;
vector<vector<int>> edge(n + 1);
for(int i = 1; i < n; ++i){
int u, v;
cin>>u>>v;
edge[u].emplace_back(v);
edge[v].emplace_back(u);
}
return edge;
}
遍历
把多叉树当作图来处理的话,由于图中是可能有环的,所以需要一个visit数组,来标记遍历过的顶点,以防止死循环。
此时一般将第一个节点,为根节点,调用方式为:
travelGraph(edge, visited, 1);
C++实现
void travelGraph(vector<vector<int>> &edge, vector<bool> &visited, int node){
if(visited[node]){
return ;
}
cout<<node<<" ";
visited[node] = true;
for(const auto &i : edge[node]){
travelGraph(edge, visited, i);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号