Pollard's rho algorithm和涉及到的两个循环检测算法
0. 简单介绍
Pollard的\(\rho\)算法是John Pollard在1975年发明的,用于分解质因数[1]。假定被分解的数为N,N的最小的质因数为\(p(p\ne N)\),那么该算法可以在\(O(\sqrt p *\alpha(N))\)的期望时间复杂度内将N分解为两个不是1的数的乘积,其中\(\alpha (N)\)是求解这两个数的最大公因数的时间复杂度,且该算法几乎不需要额外的空间
1. 核心思想
假设我们需要分解\(N=p*q\),其中p是N的一个非平凡因子,在模N的环境下生成一个近似随机的数列\(\{x_n\}\),\(x_1=2,x_i=f(x_{i-1}) mod\ N(i\ge 2)\),其中\(f(x)\)为一个多项式函数,可以取\(f(x)=x^2+1\),而2是这个模N数列的初始值:\(x_1=2,x_2=f(2)\ mod\ N,x_3=f(f(2))\ mod\ N……\)
注:据某一篇博客所言,\(f(x)=x^2+p\)是某个不知名的大佬传下来的神奇函数,会玄学般的大幅提升代码效率。
而这个模N的伪随机数列不是无限多个元素,而是在某个时刻会出现循环(不是所有的元素循环),因为这个伪随机的数列的每一个数都由前一个数唯一确定。由生日悖论,可以得出\(\{x_n\}\)出现循环节点的位置期望为\(O(\sqrt{N})\),而这个循环表示为有向图近似像字母\(\rho\),该算法也是因此而得名。
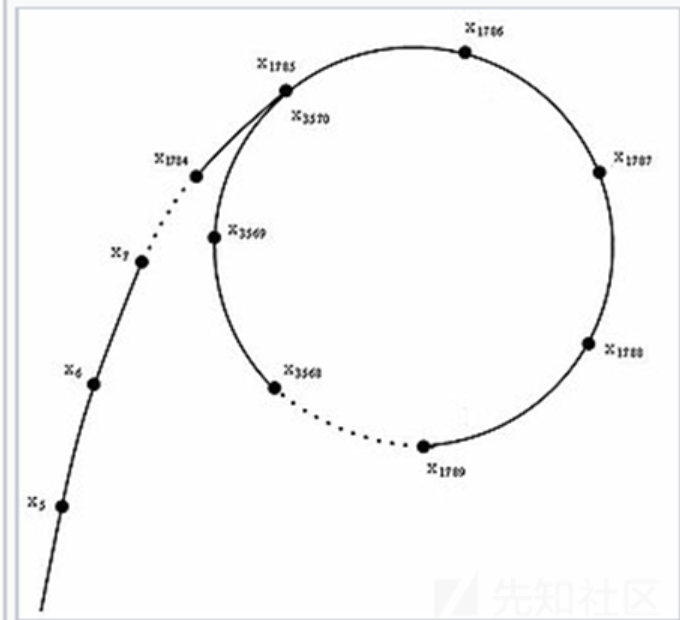
那么在另一个伪随机数组\(\{x_n\ mod\ p\},(p是N的一个素因子)\)中,存在着两个位置i,j,如果满足条件\(x_i\ mod\ p=x_j\ mod\ p,x_i\ne x_j\),那么显而易见的,有\(x_i-x_j=k*p\),那么取\(gcd(x_i-x_j,N)\),就可以得到N的一个非平凡因子。
2.基本算法流程
那么我们可以用Floyd’s cycle-finding algorithm(佛洛依德判圈算法、龟兔赛跑算法)的思想,取\(i,2i\)两个位置计算:
- 若\(gcd(x_i-x_{2i},N)=1\),那么说明\(i,2i\)不在任何数列的循环节的对应位置,继续枚举下一个i
- 若\(gcd(x_i-x_{2i},N)=N\),那么说明\(i,2i\)同时在\(\{x_i\ mod\ n\}\)和\(\{x_i\ mod\ p\}\)两个伪随机数列的循环节点上(即\(x_i-x_{2i}=k_1p=k_2n\)),同时还说明了无法再通过枚举更大的\(i\)来找到来找到满足条件的\(i\),这种情况下可以更换随机函数\(f(x)\),重新进行算法
- 若不是以上两种情况,则我们就找到了N的一个非平凡因子(p)
由于我们期望需要枚举\(O(\sqrt{p})\)个\(i\)来分解出\(N\)的一个非平凡因子\(gcd(x_i-x_{2i},N)\),\(\alpha (N)\)是求解这两个数的最大公因数的时间复杂度,那么Pollar's Rho算法能够在\(O(\sqrt{p}*\alpha(N))\)的期望时间复杂度内分解出\(N\)的一个非平凡因子
由于假定N不是质数,那么就有\(p\leq \sqrt N\),因此这个算法产生一次有效分解的期望时间复杂度也可以写为\(O(N^{\frac{1}{4}}*\alpha (N))\)
3.一个速度更快的优化
同时,该算法还有一个不常用的优化。1980年,Richard Brent 发表了一个rho算法的更快的变体,它没有改变Pollard的核心思想,但是选择了不一样的循环检测方法——Brent's cycle finding method取代了Floyd Cycle Detection Algorithm,表述如下:
注意到我们只有在\(gcd(x_i-x_{2i},N)=1\)的情况下才会继续运行算法,可以拟定一个参数\(\beta\),计算每\(\beta\)个\(x_i-x_{2i}\)的乘积对\(N\)取模的结果\(prod\),有结果:
- 若\(gcd(prod,N)=1\),则说明这\(\beta\)个\(x_i-x_{2i}\)与\(N\)的\(gcd\)均为1
- 若\(gcd(prod,N)\ne 1\),则说明找到了\(N\)的一个非平凡因子\(gcd(prod,N)\)
- 否则,即\(gcd(prod,N)=N\),这可能是因为引入了重复的因子导致了失败,并且我们也并不知道此时是否需要重新进行算法,所以需要回到\(\beta\)次操作前,进行原本的操作
此时,该算法产生一次有效分解的时间复杂度可以被优化至\(O(N^{\frac{1}{4}}+\frac{N^{\frac{1}{4}}*\alpha (N)}{\beta}+\beta *\alpha (N))\)
4.循环检测(迭代函数)
0.简介
在计算机科学中,循环检测或循环查找是在得带函数值序列中找到循环的算法问题对于任意一个函数
1. 弗洛伊德的龟兔赛跑(Floyd Cycle Detection Algorithm-Tortoise and Hare Algorithm)
如果有限状态机、迭代函数或者链表存在环,那么一定存在一个起点可以到达某个环的某处(这个起点也可以在某个环上)。
初始状态下,假设已知某个起点节点为节点S。现设两个指针t和h,将它们均指向S。
接着,同时让t和h往前推进,但是二者的速度不同:t每前进1步,h前进2步。只要二者都可以前进而且没有相遇,就如此保持二者的推进。当h无法前进,即到达某个没有后继的节点时,就可以确定从S出发不会遇到环。反之当t与h再次相遇时,就可以确定从S出发一定会进入某个环,设其为环C。
如果确定了存在某个环,就可以求此环的起点与长度。
上述算法刚判断出存在环C时,显然t和h位于同一节点,设其为节点M。显然,仅需令h不动,而t不断推进,最终又会返回节点M,统计这一次t推进的步数,显然这就是环C的长度。
为了求出环C的起点,只要令h仍均位于节点M,而令t返回起点节点S,此时h与t之间距为环C长度的整数倍。随后,同时让t和h往前推进,且保持二者的速度相同:t每前进1步,h前进1步。持续该过程直至t与h再一次相遇,设此次相遇时位于同一节点P,则节点P即为从节点S出发所到达的环C的第一个节点,即环C的一个起点。
——Wiki百科-Floyd判圈算法
分析:
从S(这个点是\(\rho\)的尾巴末端而不是在圆上)开始,到t和h相遇(假设它们可以相遇),设S到循环起点P的距离为m,循环起点P到相遇位置M的距离为n(在一圈之内),一圈的路程为a,那么可以得到t和h走过的路程为:
又已知h的速度是t的速度的两倍,易知h走过的路程也是t的两倍,有:
所以:
那么当t回到S点,h在M点(h点是继续按照原有的方向走下去,可以认为t和h的行进方向相同,只不过一个在\(\rho\)的尾巴上前进,另一个则在圆圈上前进,这样即使前进方向和速度一样,也会相遇),各自向前以每次一个单位的速度移动,当t走过m个单位到达P点时,h也走过了m个单位,而M点本身距离P点有n个单位长度,则h现在距离P点有m+n个单位长度,即回到了P点,所以t和h会在这个P这个循环起点上相遇。
时间复杂度:
注意到当指针t到达环C的循环起点节点P时(此时指针h显然在环C上),之后指针t最多仅可能走1圈。若设节点S到P距离为\(m\),环C的长度为\(n\),则时间复杂度为\(O(m+n)\),是线性时间的算法。
空间复杂度:
仅需要创立指针t、指针h,保存环长n、环的一个起点P。空间复杂度为\(O(1)\),是常数空间的算法。
布伦德的传送乌龟(Brent’s Cycle Detection-The Teleporting Turtle)
原理:t和h从起点S出发,t先不动,h每次只走一个单位,在第i次中最多可以走\(2^i\)步,当步数到达步数上限时进入第i+1次。也即在第i次迭代中,最长可以走\(2^i\)个单位长度,\(2^i\)九十步数的上限。h每走出一步,判断是否遇到了t,如果没有则继续,直到达到步数上限,将t传送到h处,然后继续进行直到h与t相遇
环长:h走了几步遇到t,环长就是几
环起点:Flyod判圈算法利用了乌龟和兔子的距离是环长整数倍的性质求起点,所以可以让乌龟回到起点,兔子回到距离起点环长距离的节点,随后与Floyd算法一样
int *t = head, *h = head;
int steps_taken = 0, steps_limit = 2;
while(True)
{
if(h == null)
break; // No Loop
++steps_taken;
if(h == t)
break; // Found Loop;
if(steps_taken == step_limit)
{
steps_taken = 0;
step_limit *= 2;
t = h; // teleport the t;
}
}
时间复杂度:\(O(n)\),线性复杂度,并且比Flyod好
空间复杂度:\(O(1)\)常数空间
参考文章:
- 密码学学习笔记 之 浅析Pollard's rho algorithm及其应用
- 【学习笔记】Pollard's rho算法
- Cycle detection
- Floyd判圈算法
- 判圈算法(Flyod、Brent's)
在数论中指能整除给定正整数的质数 ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号