【模板】扩展KMP

该博客转载自：https://blog.csdn.net/dyx404514/article/details/41831947

为了方便自己理解，添加到该随笔归类。如有需要，请阅读原博客。

 

扩展KMP解决问题：

定义母串S，字符串T，S的长度为n，T的长度为m。求T与S的每一个后缀的最长公共前缀。

即设extend数组，extend[i]表示T与S[i,n-1]的最长公共前缀，求出所有的extend[i](0<= i < n)

 

为什么叫扩展KMP？

如果有一个位置的extend[i] = m ，则表示T在S的位置i上出现，就是标准的KMP，所以是对KMP的扩展。

 

举例说明：

S  = “aaaabaa”，T = “aaaaa”，首先计算extend[0]，需要进行5次匹配，直到发生失配。

 

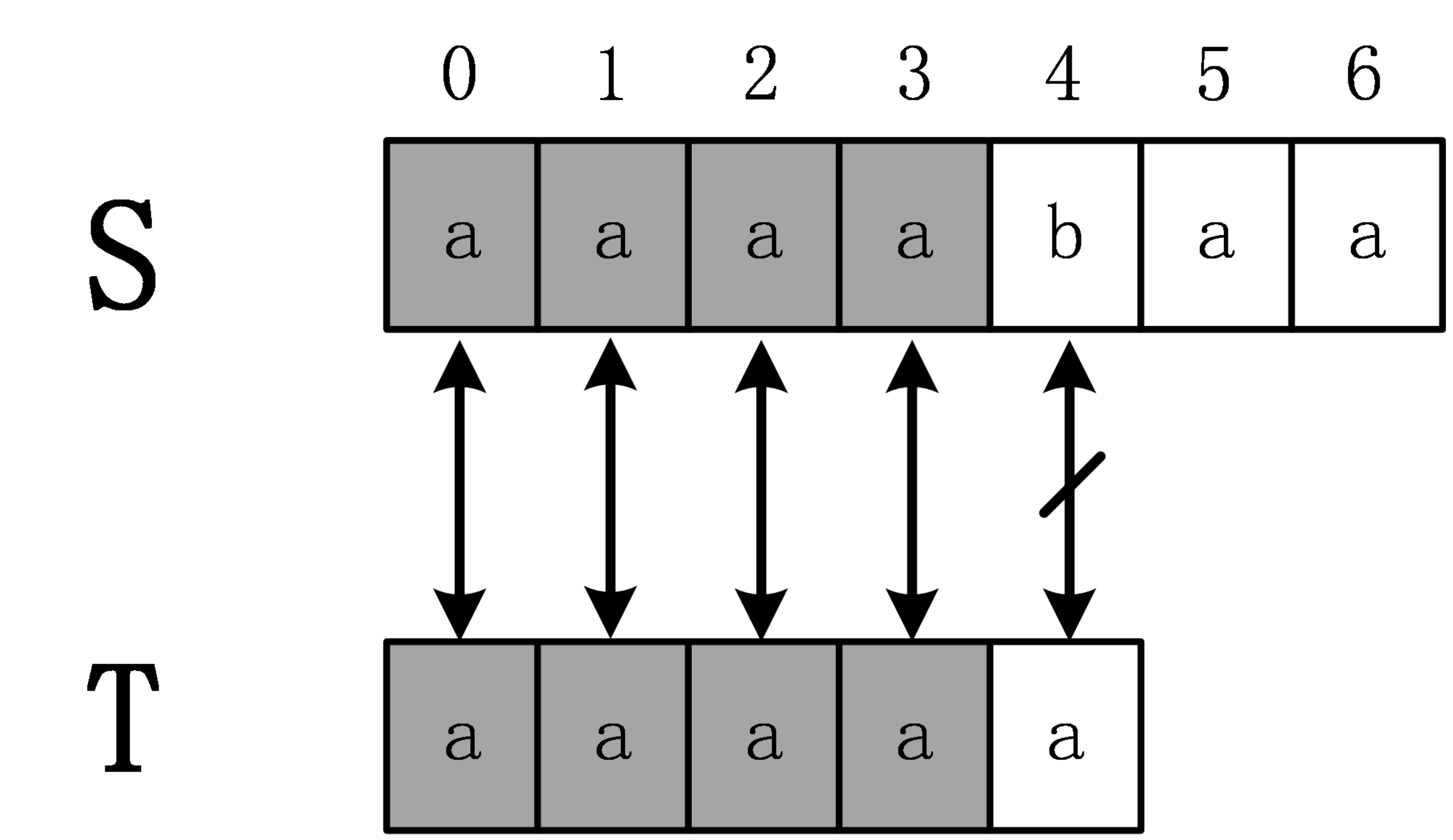
遍历易得extend[0] = 4，下面计算extend[1]

根据KMP的基本思想，计算下一个extend的时候是不需要再对前面的内容进行重新匹配的，思想类似于KMP进行分析：

通过extend[0] = 4 ，可以得出S[0,3] = T[0,3]，因为计算extend[1]时，是从S[1]开始匹配的，所以可以得S[1.3] = T[1.3]

设置一个辅助数组next[i]，表示T[i,m-1]和T的最长公共前缀的长度。

在此例中，next[1] = 4，即T[0,3] = T[1,4]，进一步推导出 T[1,3] = T[0,2]，根据前面的已知条件，可以得到：S[1,3] = T[0,2]

故下一次匹配时，前面3个字符不需要再进行匹配，直接匹配S[4] 和 T[3]即可。此时匹配失配，所以extend[1] = 3。

 

时间复杂度分析：

O(n+m)

 

模板代码：

const int maxn = 2e7+5;
char s[maxn],t[maxn];
int next[maxn],extend[maxn];
void getNext(char t[]){
    int i=0,po,len=strlen(t);
    next[0] = len;
    while(t[i] == t[i+1] && i+1 < len)
        i++;
    next[1]=i;
    po = 1;
    for(i = 2;i < len;i ++){
        if(next[i-po]+i < next[po]+po)
            next[i] = next[i-po];
        else{
            int j=next[po]+po-i;
            if(j<0) j=0;
            while(i+j<len && t[j]==t[j+i])
                j++;
            next[i]=j;
            po=i;
        }
    }
}
void getExtend(char s[], char t[]){
    int i=0,po,n=strlen(s),m=strlen(t);
    getNext(t);
    while(s[i]==t[i] && i<m && i<n)
        i++;
    extend[0] = i;
    po=0;
    for(i = 1; i < n;i++){
        if(next[i-po]+i < extend[po]+po)
            extend[i] = next[i-po];
        else{
            int j=extend[po]+po-i;
            if(j < 0) j = 0;
            while(i+j<n && j<m && s[j+i] == t[j])
                j++;
            extend[i] = j;
            po=i;
        }
    }
}