选自 11 月做题笔记。

这题真没啥思维含量吧，非常容易想到先考虑什么时候怪物会被抓住（后面是我的思考过程）：

（\(1\)）只有一个点，此时怪物必然在这个点上，直接选这个点怪物就必然被抓住。

（\(2\)）树形如一条链，此时考虑从链的一头开始，按照顺序依次选链的每一个点。

此时假设当前已经按顺序选中了链的第 \(1\ldots i-1\) 点，此时怪物必然只能在 \(i\sim n\) 的点上。而若你此时选择了 \(i\) 点，则：

• 若怪物在 \(i\) 点，则怪物必死。
• 否则，怪物仍然只能被困在 \(i+1\sim n\) 点上。

因此这个策略一定能杀死怪物。

（\(3\)）树形如一个菊花图，即对于每个 \(2\le i\le n\) 都存在一条 \(1\leftrightarrow i\) 边。此时你有下面的策略：

• 选中 \(1\) 点，此时怪物一定在某个结点上。
• 选中 \(2\) 点（叶子点），此时怪物一定不能在 \(2\) 点上。
• 再次选中 \(1\) 点，此时怪物不能在 \(1\) 点上，同时也无法前往 \(2\) 点。
• 选中 \(3\) 点，此时怪物同时不能出现在 \(2,3\) 点上。
• 再次选中 \(1\) 点……
• 选中 \(n\) 点，此时怪物同时不能出现在 \(2,3,4,\ldots,n\) 点上。
• 选中 \(1\) 点，此时怪物必死。

因此这个策略一定能杀死怪物。

（\(4\)）如果我在菊花图上挂一条链怎么样？？？

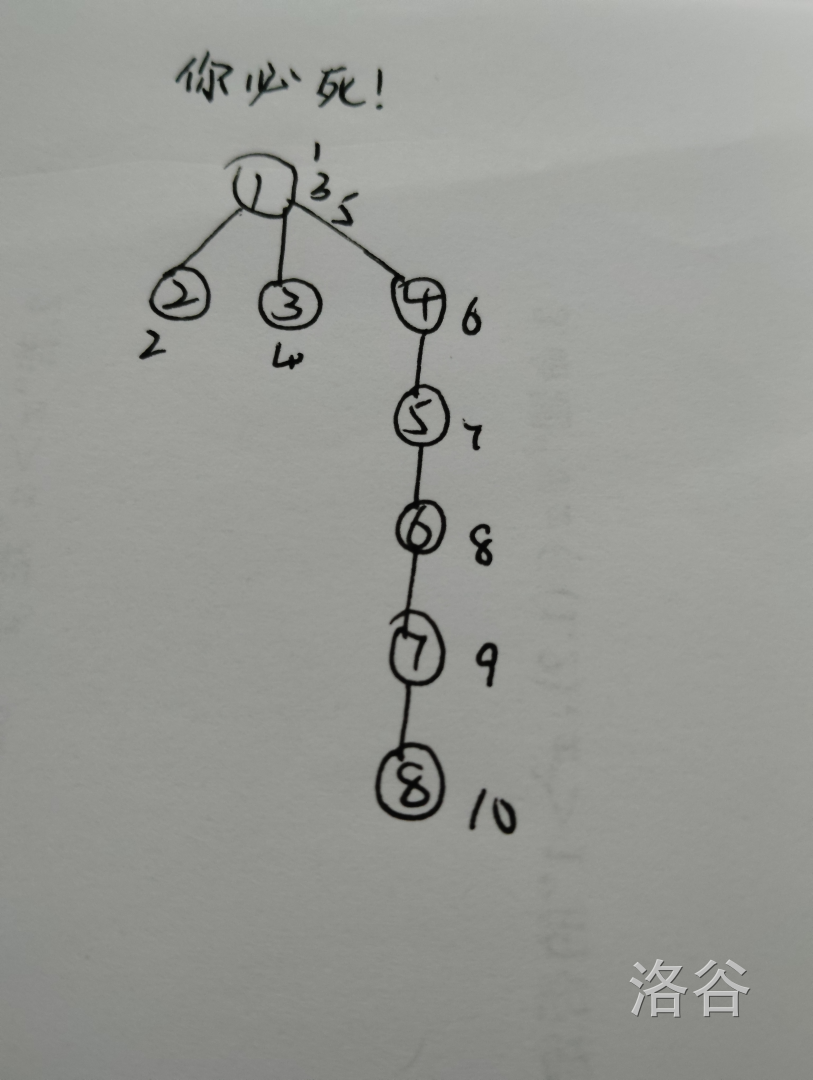
按照上图中给结点标号的顺序即可杀死怪物。策略即为：先在菊花上操作，把怪物逼到一条链上，然后按照链的策略击杀怪物。

（\(5\)）如果我在菊花图上挂多条链，得到一个毛毛虫树怎么样？

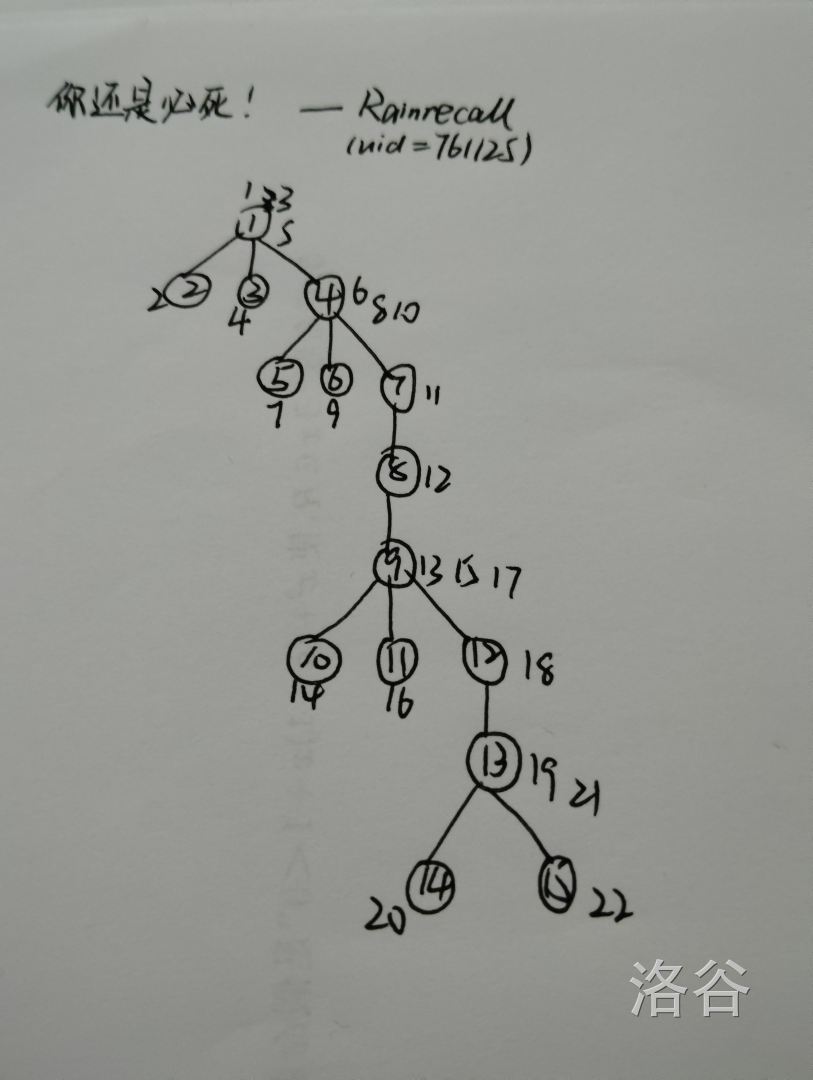
按照上图给结点标号的顺序即可杀死怪物。策略即为：找出毛毛虫树上的中心链（在上图中即为 \(1-4-7-8-9-12-13\)），然后从上往下，若当前结点相邻的结点有叶子节点，那么就先用菊花图的策略把所有叶子结点干掉。然后用链的策略把当前结点也干掉继续往下递归，直到干完中心链上的所有点以及所有叶子结点为止。容易证明该策略必然正确。

（\(6\)）如果在毛毛虫树的一个叶子结点上再加一个儿子，那又会怎么样？

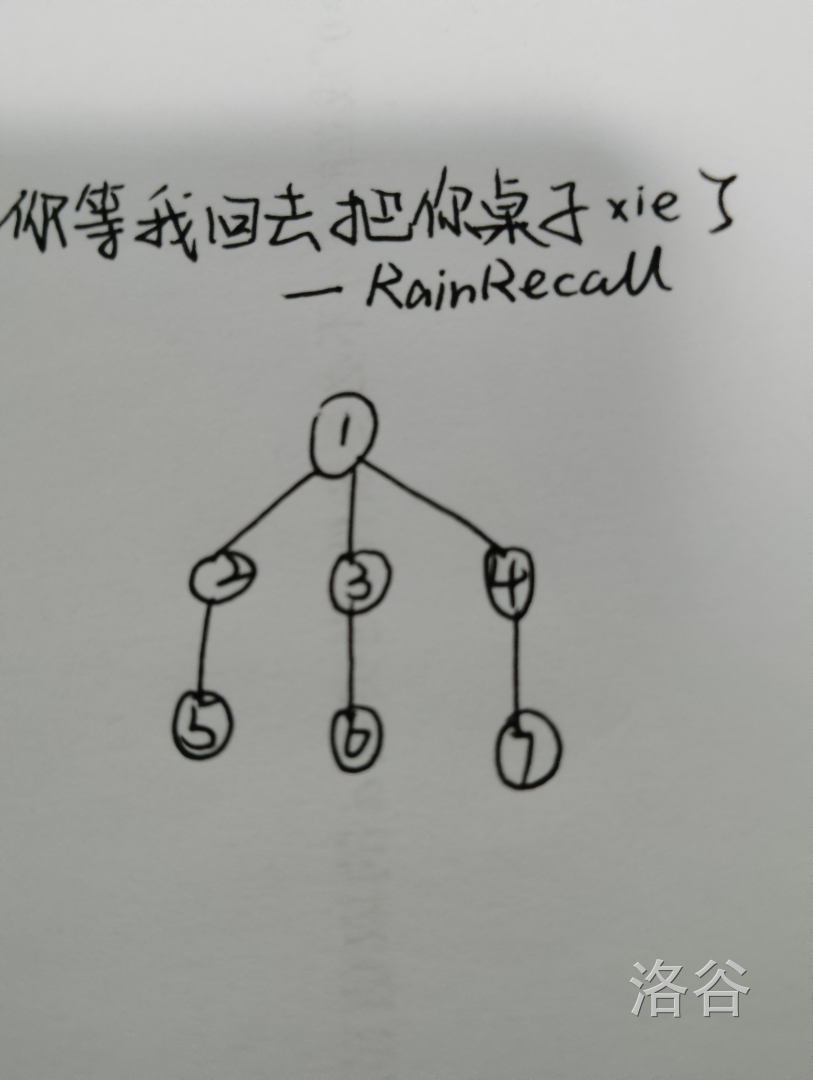
注意到此时不存在一个能让怪物一定必死的策略，那只能下课死了（确信

然后容易观察到结论：若一个树的一个导出子图不能让怪物必死，那么这个树一定不能让怪物必死。然后你发现剩下满足条件的情况都是毛毛虫树，于是就容易得到 \(O(nq)\) 的求解方法（即判断在区间 \([l,r]\) 内的边是否构成了一个毛毛虫树森林）。

然后考虑优化。注意到在固定左端点的时候移动右端点存在单调性（即若 \([l,r]\) 不合法，则 \([l,r+1]\) 一定不合法；\([l,r]\) 合法，则 \([l,r-1]\) 一定合法）。

因此考虑处理出 \(f\) 数组：\(f_i\) 表示若当前左端点为 \(i\)，则右端点最大为 \(f_i\) 可以保证边在 \([i,f_i]\) 区间内，一定合法（即能让怪物必死）。于是容易想到双指针维护答案，每一次插入 \(r+1\) 位置的元素直到当前区间内的边不再合法，更新 \(f\) 数组的值然后删除 \(l\) 位置的元素。

问题在于如何快速的判断一个区间是否是合法的。考虑一个森林是毛毛虫森林的充要条件。容易观察到：

• 一个森林是毛毛虫森林，当且仅当对于森林上任意一点，都不存在超过 \(2\) 个和其相邻的结点不为叶子结点（即度数 \(\ge 2\)）。

于是考虑从度数方面入手，动态维护若加入 / 删除当前区间内的边，森林是否仍然为 / 不为毛毛虫森林。直接加入一个点可能存在后效性（加入一个点 \(x\)，此时 \(x\) 必然为叶子结点，则其会影响和她相邻的唯一结点 \(y\) 的信息，而 \(y\) 又会影响到和其相邻的另一个点 \(w\) 的信息），维护起来比较麻烦。然后我编了一个奇奇怪怪的做法，又维护了另一个数组信息，表示每个点相邻的点在当前导出子图中的点编号的异或，根据异或的一些性质，可以快速的找出后效性产生的结点 \(w\)，而这个数组也同样是容易维护的。

于是这个题就做完了，时间复杂度根据实现优劣可以为 \(O(n+m+q)\) 或 \(O(n+m\log n+q)\)，均可通过该题。