信号完整性（SI）电源完整性（PI）学习笔记（六）电感的物理基础（一）

电感的物理基础
1.电感的定义：通常是指由导线绕成的线圈或螺线杆的电感，其中有磁力线通过。或者说对表面磁场强度的数值积分。
2.电感三个基本法则：
（1）电流周围会形成闭合磁力线匝数；
（2）电感是导体电流1A时周围的磁力线匝数；
（3）周围磁力线匝数改变时，导体两边产生感应电压。

3.我们以韦伯Wb为单位计算电流周围的磁力线匝数，但是磁力线受很多因素的影响：
（1）导体中电流的大小影响电流周围磁力线匝数，电流越大磁力线匝数就会增加；
（2）导体长度越长，磁力线匝数就越多；
（3）导体的横截面积也影响磁力线匝数，但是这是个二阶效应，比较复杂；
（4）附近其他电流的存在也会对第一个电流周围的磁力线匝数产生影响；
（5）计算第一条导线周围的磁力线匝数时，总要把自身的磁力线匝数和返回路径的磁力线匝数相叠加。

4.电感是通过单位安培电流时其周围的磁力线圈韦伯数大小的度量：

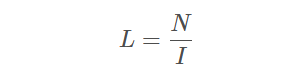
其中：
L 表示电感，单位为 H
N 表示导体周围的磁力线匝数，单位为 Wb
I 表示导体中的电流，单位为A

若通过导体的电流加倍，磁力线的匝数也会加倍，但二者比率不变，且该比率与通过导体的电流完全无关。同样，磁力线的匝数改变时，表示这一比率的电感依然不变。

5.我们把一条导线自身电流产生的磁力线圈称为自磁力线圈，把由邻近电流产生的磁力线圈称为互磁力线圈。
6.自感是指导线中流过单位安培电流时，所产生的环绕在导线自身周围的磁力线匝数。
7.同理，互感是指一条导线中流过单位安培电流时，所产生的的环绕在另一条导线周围的磁力线匝数；
（1）互感具有对称性；
（2）两条导线之间的互感小于二者中任一个的自感。

8.一段导线周围的磁力线匝数发生变化，导线两端就会产生感应电压。
磁力线圈有一个特殊性质：不管什么原因，只要一段导线周围的磁力线总匝数发生变化，导线两端就会产生电压。该电压与磁力线总匝数变化的快慢有着直接关系：

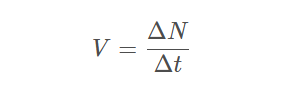
其中：
V 表示导线两端的感应电压
ΔN 表示磁力线匝数的变化量
Δt 表示磁力线匝数变化的时间

如果导线中的电流发生变化，则其周围的自磁力线圈的匝数也将变化，从而在导线两端产生电压。导线周围的磁力线匝数为N=L×I, 其中 L 是这段导线的自感。于是，导线两端所产生的电压（即感应电压）与导线的电感和导线中电流变化的快慢有关：

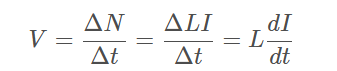
这个由电流变化产生的感应电压引起传输线效应、突变、串扰、开关噪声、轨道塌陷、地弹和大多数电磁于扰源(EMI)。感应电压正是信号完整性中意义重大的根本原因，如果电流变化时，没有感应电压产生，信号就不会受到电感的影响。

9.互磁力线匝数的变化在第一条导线的两端产生感应电压，另一条导线中的电流发生变化时，我们用串扰来描述，邻近导线上产生的感应电压噪声：

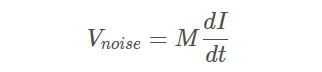
其中：
Vnoise​ 表示第一根导线中的感应电压噪声
M 表示两根导线之间的万感
I 表示第二根导线中的电流

10.感应电压取决于电流变化的速度，所以有时候用开关噪声或 ΔI 噪声来描述电感线圈中电流切换时产生的噪声。
11.局部电感：
在计算磁力线圈的时候，假设这段导线所属的电流回路的剩余部分中不存在电流。由于仅考虑了电流回路的一部分，而且假设回路的其他部分不存在电流，所以把这种电感称为局部电感。一定要记住，当谈到局部电感时，回路的其他部分是不存在的。
分类：
（1）局部自感
（2）局部互感
对于直环形导线，值用简单的近似所计算的局部自感，其精度优于几个百分点，近似式如下：

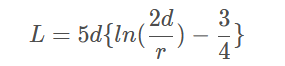
其中：
L 表示导线的局部自感，单位为 nH
r 表示导线的半径，单位为in
d 表示导线的长度，单位为 in

重要特性：局部自感的一个重要特性：电流分布越分散，局部电感就越小。反之， 电流分布密度越大，局部电感就越大。

两根直的圆导线的局部互感可以近似为：

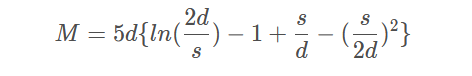
其中：
M 表示导线间的局部互感，单位为 nH
d 表示两圆杆的长度，单位为 in
s 表示两导线的中心距，单位为in

上述这个繁琐公式考虑到了二阶效应，一般认为它是二阶模型。当 s«d 时，即中心距相对于圆杆长度很小时，此公式可以进一步近似简化为：

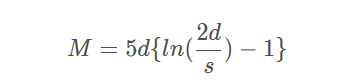
这是个一阶模型，忽略了两圆杆之间远距离耦合的一些细节，是以牺牲精确度来简化计算的。
当两个导线段间距远大于导线长度时，两段导线间的局部互感小于任一段导线局部自感的10%, 这时互感通常可以忽略不计。