计算几何基础
向量
定义(摘自 OI-wiki)
向量:既有大小又有方向的量称为向量。数学上研究的向量为 自由向量,即只要不改变它的大小和方向,起点和终点可以任意平行移动的向量。记作 \(\vec a\) 或 \(\boldsymbol{a}\)。
有向线段:带有方向的线段称为有向线段。有向线段有三要素:起点,方向,长度,知道了三要素,终点就唯一确定。一般使用有向线段表示向量。
向量的模:有向线段 \(\overrightarrow{AB}\) 的长度称为向量的模,即为这个向量的大小。记为:\(|\overrightarrow{AB}|\) 或 \(|\boldsymbol{a}|\)。
零向量:模为 \(0\) 的向量。零向量的方向任意。记为:\(\vec 0\) 或 \(\boldsymbol{0}\)。
单位向量:模为 \(1\) 的向量称为该方向上的单位向量。一般记为 \(\vec e\) 或 \(\boldsymbol{e}\)。
平行向量:方向相同或相反的两个 非零 向量。记作:\(\boldsymbol a\parallel \boldsymbol b\)。对于多个互相平行的向量,可以任作一条直线与这些向量平行,那么任一组平行向量都可以平移到同一直线上,所以平行向量又叫 共线向量。
相等向量:模相等且方向相同的向量。
相反向量:模相等且方向相反的向量。
向量的夹角:已知两个非零向量 \(\boldsymbol a,\boldsymbol b\),作 \(\overrightarrow{OA}=\boldsymbol a,\overrightarrow{OB}=\boldsymbol b\),那么 \(\theta=\angle AOB\) 就是向量 \(\boldsymbol a\) 与向量 \(\boldsymbol b\) 的夹角。记作:\(\langle \boldsymbol a,\boldsymbol b\rangle\)。显然当 \(\theta=0\) 时两向量同向,\(\theta=\pi\) 时两向量反向,\(\theta=\frac{\pi}{2}\) 时两向量垂直,记作 \(\boldsymbol a\perp \boldsymbol b\),并且规定 \(\theta \in [0,\pi]\)。
注意到平面向量具有方向性,两个向量不能比较大小(但可以比较两向量的模长)。但是两个向量可以相等。
向量坐标表示:对于向量 \(\boldsymbol{a}\) ,令 \(\overrightarrow{OA}=\boldsymbol{a}\) ,则 \(A\) 的坐标为 \(\boldsymbol{a}\) 的坐标表示。
向量运算
向量加减法
满足四边形定则/三角形定则
向量点乘
定义:$\boldsymbol{a}\cdot \boldsymbol{b}=|\boldsymbol{a}|\cdot |\boldsymbol{b}|\cos \langle \boldsymbol{a},\boldsymbol{b}\rangle $
性质:
计算出来的结果是个标量,有以下性质:
应用:
-
判定两向量垂直:
\[\boldsymbol{a} \perp \boldsymbol{b} \iff \boldsymbol{a} \cdot \boldsymbol{b} = 0 \]即互相垂直的两个向量的内积,结果为 \(0\);向量与零向量内积,结果为 \(0\)。如果使用内积为零作为垂直的定义,则可以得出零向量与任何向量都垂直。
-
判定两向量共线:
\[\exists\lambda \in \mathbf{R} (\boldsymbol{a} = \lambda \boldsymbol{b}) \iff |\boldsymbol{a} \cdot \boldsymbol{b}| = |\boldsymbol{a}| |\boldsymbol{b}| \] -
计算向量的模:
\[|\boldsymbol a| = \sqrt{\boldsymbol{a} \cdot \boldsymbol{a}} \] -
计算两向量的夹角:
\[\theta = \arccos \frac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol a| |\boldsymbol b|} \]
点乘坐标表示:
向量叉乘
定义:
- \(|\boldsymbol{a} \times \boldsymbol{b}| = |\boldsymbol{a}| |\boldsymbol{b}| \sin \langle \boldsymbol{a}, \boldsymbol{b} \rangle\);
- \(\boldsymbol{a} \times \boldsymbol{b}\) 与 \(\boldsymbol{a}, \boldsymbol{b}\) 都垂直,且 \(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{a} \times \boldsymbol{b}\) 的方向符合右手法则。
- 在平面直角坐标系中,虽然无法体现出 \(z\) 轴,但是叉乘出来的向量只可能是两个方向中一种,于是我们使用正负表示方向。
性质
-
外积是关于两个向量分别都线性的双线性运算。具体而言,外积满足:
\[\begin{aligned} (\boldsymbol{a} + \boldsymbol{b}) \times \boldsymbol{c} &= \boldsymbol{a} \times \boldsymbol{c} + \boldsymbol{b} \times \boldsymbol{c} \\ \boldsymbol{a} \times (\boldsymbol{b} + \boldsymbol{c}) &= \boldsymbol{a} \times \boldsymbol{b} + \boldsymbol{a} \times \boldsymbol{c} \\ (\lambda \boldsymbol{a}) \times \boldsymbol{b} &= \lambda (\boldsymbol{a} \times \boldsymbol{b}) \\ \boldsymbol{a} \times (\lambda \boldsymbol{b}) &= \lambda (\boldsymbol{a} \times \boldsymbol{b}) \end{aligned} \]前两行性质亦可称为分配律,即外积对于向量加法满足乘法分配律。
-
外积满足反交换律,即:
\[\boldsymbol a \times \boldsymbol b=-\boldsymbol b \times \boldsymbol a \] -
根据上文内积与外积的几何定义:
\[\begin{aligned} |\boldsymbol a \times \boldsymbol b| &= |\boldsymbol a| |\boldsymbol b| \sin \langle \boldsymbol a, \boldsymbol b \rangle \\ \boldsymbol a \cdot \boldsymbol b &= |\boldsymbol a| |\boldsymbol b| \cos \theta \\ &= |\boldsymbol a| |\boldsymbol b| \cos \langle \boldsymbol a, \boldsymbol b\rangle \end{aligned} \]可以写出恒等式:
\[(\boldsymbol a\times \boldsymbol b) \cdot (\boldsymbol a\times \boldsymbol b) = |\boldsymbol a|^2 |\boldsymbol b|^2-{(\boldsymbol a \cdot \boldsymbol b)}^2 \] -
外积满足 Jacobi 恒等式:
\[\boldsymbol a \times (\boldsymbol b \times \boldsymbol c) + \boldsymbol b \times (\boldsymbol c \times \boldsymbol a) + \boldsymbol c \times (\boldsymbol a \times \boldsymbol b) = \boldsymbol 0 \]
应用
-
判定两向量是否共线:
\[\exists\lambda \in \mathbf{R} (\boldsymbol{a} = \lambda \boldsymbol{b}) \iff \boldsymbol{a} \times \boldsymbol{b} = \boldsymbol{0} \]即共线的两个三维向量的外积,结果为 \(\boldsymbol 0\);三维向量与自身外积,结果为 \(\boldsymbol 0\);三维向量与零向量外积,结果为 \(\boldsymbol 0\)。若使用外积为零作为两向量共线的定义,则可以得出零向量与任何向量都共线。
-
计算两向量张成的平行四边形面积:
\[S \langle \boldsymbol a, \boldsymbol b \rangle = |\boldsymbol a \times \boldsymbol b| \] -
判断两向量方向:
记 \(\boldsymbol{a} = (m, n), \boldsymbol{b} = (p, q)\),将平面直角坐标系扩充为空间直角坐标系,原平面位于新坐标系的 \(xOy\) 平面,原本的坐标 \((m, n)\) 和 \((p, q)\) 变为 \((m, n, 0)\) 和 \((p, q, 0)\)。
那么两个向量的外积为 \((0, 0, mq - np)\),因此平行四边形的面积为 \(|mq - np|\),可以视为二阶行列式运算结果的绝对值。
此时,根据右手法则和 \(z\) 坐标的符号,可以推断出 \(\boldsymbol b\) 相对于 \(\boldsymbol a\) 的方向,若在逆时针方向则 \(z\) 坐标为正值,反之为负值,简记为 顺负逆正。
叉乘坐标表示:
杂项
极角排序
方法一:atan2
直接用 atan2 函数算出极角,然后排序。
但是当这个点是原点的时候 atan2 是未定义,可能会报 UB.
要注意 atan2 的第一个参数是 y
方法二:向量叉积
用叉积判断方向,代码:
bool pmc(Node x,Node y){return cross(x,y)>0||(cross(x,y)==0&&x.len()<y.len());}
直线夹角
方法一:向量点乘
用向量表示两直线,设两个向量为 \(\bf{a}\),\(\bf{b}\) ,夹角为 \(\theta\).
有 \(\theta =\arccos\frac{\bf{a}\cdot {b}}{|\bf{a}|\cdot|{b}|}\) .
方法二:atan2
直接算出两个向量的极角,相减即可。
直线交点
面积比 \(\to\) 线段比 \(\to\) 定比分点
设两条直线的两个点分别为 \(A_1,A_2,B_1,B_2\) ,交点为 \(C\)
令 \(\boldsymbol{a}=\overrightarrow{OA_2}-\overrightarrow{OA_1}\) ,\(\boldsymbol{b}=\overrightarrow{OB_2}-\overrightarrow{OB_1}\) ,\(\boldsymbol{c}=\overrightarrow{OB_1}-\overrightarrow{OA_1}\)
令 \(t=\frac{b\cdot c}{b\cdot a}\)
所以 \(\overrightarrow{OC}=\overrightarrow{OA}+t\boldsymbol{a}\)
两圆交点
关于求两圆交点
先判掉包含和分离的情况,只考虑相交
如图:
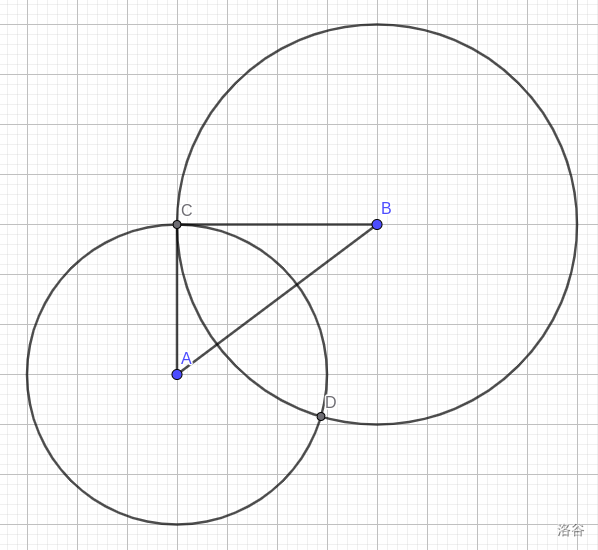
先求出 $\overrightarrow{AB} $ 的辐角设为 \(\theta\) 令 $\angle CAB=\alpha $
所以 $\cos \alpha =\frac{r_12+\overline{AB}2-r_2^2}{2r_1\cdot \overline{AB} } $
所以 \(C(x_A+r_1\cos(\theta+\alpha),y_A+r_1\sin(\theta+\alpha)),D(x_A+r_1\cos(\theta-\alpha),y_A+r_1\cos(\theta-\alpha))\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号