数据结构

笛卡尔树

P5854 【模板】笛卡尔树

笛卡尔树是一种二叉树，每一个节点由一个键值二元组 \((k,w)\) 构成．要求 \(k\) 满足二叉搜索树（BST）的性质，而 \(w\) 满足堆的性质．如果笛卡尔树的 \(k,w\) 键值确定，且 \(k\) 互不相同，\(w\) 也互不相同，那么这棵笛卡尔树的结构是唯一的．

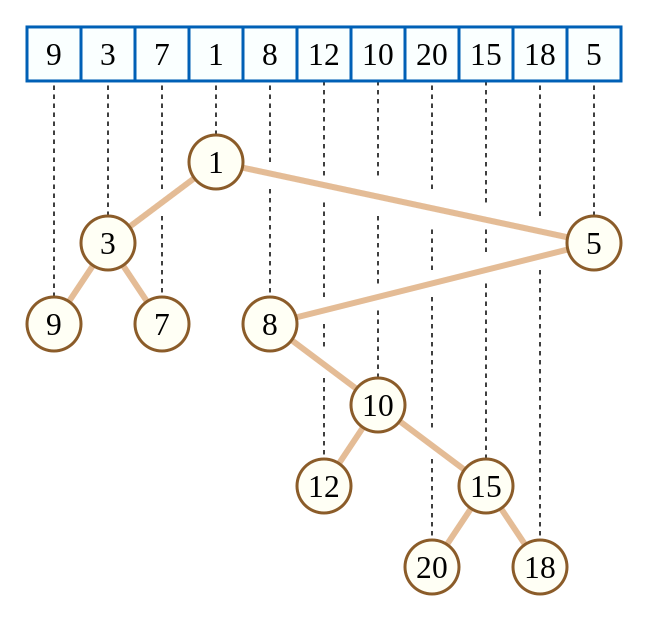
我们考虑将元素按 \(k\) 升序依次插入到当前的笛卡尔树中．

对于一棵笛卡尔树，定义「右链」为从根节点开始一直走右儿子，走到叶节点形成的链．则插入节点后，这个节点一定在右链上．因为是按照满足 BST 性质的 \(k\) 升序插入，那么这个新插入的节点必然在树的 最右端．这个节点不可能是一个左儿子，也没有右儿子．

于是我们从下往上比较右链节点与当前节点 \(u\) 的 \(w\)，如果找到一个右链上的节点 \(x\) 满足 \(w_x<w_u\)，就把 \(u\) 接到 \(x\) 的右儿子上，而 \(x\) 原本的右子树就变成 \(u\) 的左子树．

显然每个数最多进出右链一次（或者说每个点在右链中存在的是一段连续的时间）．这个过程可以用单调栈维护，栈中维护当前笛卡尔树的右链上的节点．一个点不在右链上了就把它弹掉．这样每个点最多进出一次，复杂度 \(O(n)\)．

代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e7+10;
int n,a[N],b[N],h;
ll x,y,l[N],r[N];
void build(){
	for(int i=1;i<=n;i++){
		while(h&&a[b[h]]>a[i]) h--;
		if(!h) l[i]=b[1];
		else l[i]=r[b[h]],r[b[h]]=i;
		b[++h]=i;
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	build();
	for(int i=1;i<=n;i++){
		x^=i*(l[i]+1);
		y^=i*(r[i]+1); 
	}
	cout<<x<<' '<<y;
	return 0;
}

李超线段树

P4097 【模板】李超线段树 / [HEOI2013] Segment

应用：P8726 [蓝桥杯 2020 省 AB3] 旅行家，P4254 [JSOI2008] Blue Mary 开公司，P3081 [USACO13MAR] Hill Walk G，P11958 「ZHQOI R1」划分，P6047 丝之割

（我们发现但凡用斜率优化 dp 做的题一般都能用李超线段树，而且比斜率优化好想好写）

要求在平面直角坐标系下维护两个操作（强制在线）：

1. 在平面上加入一条线段．记第 \(i\) 条被插入的线段的标号为 \(i\)，该线段的两个端点分别为 \((x_0,y_0)\)，\((x_1,y_1)\)．

2. 给定一个数 \(k\)，询问与直线 \(x = k\) 相交的线段中，交点纵坐标最大的线段的编号（若有多条线段与查询直线的交点纵坐标都是最大的，则输出编号最小的线段）．特别地，若不存在线段与给定直线相交，输出 \(0\)．

数据满足：操作总数 \(1 \leq n \leq 10^5\)，\(1 \leq k, x_0, x_1 \leq 39989\)，\(1 \leq y_0, y_1 \leq 10^9\)．

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,p=39989,p1=1e9;
const double eps=1e-14;
int ans,idx,cnt;
struct node{
	long double k=0,b=0;
}q[4*N];
struct Node{
	int id=0;
}tr[4*N];
bool check(int i,int j,int x){
	if(i==0) return false;
	if(j==0) return true;
	if(abs(q[i].k*x+q[i].b-(q[j].k*x+q[j].b))<eps) return i<j;
	return q[i].k*x+q[i].b>(q[j].k*x+q[j].b);
}
void insert(int x,int y,int x1,int y1){
	idx++;
	if(x==x1) q[idx].k=0,q[idx].b=max(y,y1);
	else q[idx].k=1.0*(y1-y)/(x1-x),q[idx].b=y-q[idx].k*x;
}
void modify(int x,int l,int r,int ql,int qr,int id){
	if(r<ql||qr<l) return;
	int mid=(l+r)>>1;
	if(l>=ql&&r<=qr){
		bool a=check(id,tr[x].id,l),b=check(id,tr[x].id,r),c=check(id,tr[x].id,mid);
		if(tr[x].id==0){
			tr[x].id=id;
			return;
		}
		if(a&&b){//插入到这条线完全优于之前的，直接替换 
			tr[x].id=id;
			return;
		}
		if(!a&&!b) return;//完全劣于之前的，不管它
		if(c) swap(id,tr[x].id);
		if(a!=c) modify(x*2,l,mid,l,r,id);
		else modify(x*2+1,mid+1,r,l,r,id);		
		return;
	}
	if(ql<=mid) modify(x*2,l,mid,ql,qr,id);
	if(qr>mid) modify(x*2+1,mid+1,r,ql,qr,id);
}
int query(int x,int l,int r,int id){
	if(l==r) return tr[x].id;
	int mid=(l+r)>>1,res;
	if(id<=mid) res=query(x*2,l,mid,id);
	else res=query(x*2+1,mid+1,r,id);
	if(check(tr[x].id,res,id)) res=tr[x].id;
	return res;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n,k,op;
	int x,y,x1,y1;
	cin>>n;
	while(n--){
		cin>>op;
		if(op==0){
			cin>>k;
			x=(k+ans-1)%p+1;
			ans=query(1,1,p,x);
			cout<<ans<<"\n";
		}
		else{
			cin>>x>>y>>x1>>y1;
			x=(x+ans-1)%p+1,y=(y+ans-1)%p1+1,x1=(x1+ans-1)%p+1,y1=(y1+ans-1)%p1+1;
			if(x>x1) swap(x,x1),swap(y,y1);
			insert(x,y,x1,y1);
			modify(1,1,p,x,x1,idx);
		}
	}
	return 0;
}