笔记:动态规划 之 入门与线性DP
Part -1 -迷惑性引入
动态规划算法通常用于求解具有某种最优性质的问题。
那它和贪心有区别吗?
当然有。不然叫动态规划干啥?
幼儿园英语老师:DP是啥?
小盆友:Dog&Peppa pig
英语老斯:恩恩!真聪明!
然而,你是小盆友吗?
如果是

如果不是,

DP是D****** P*******的缩写。
意思是动态规划。
聪明的***告诉你:是Dynamic Programming的缩写!!!
我到底为什么写引入...
Part 0 - DP 入门
一、 用途
动态规划 \((Dynamic programming,简称 DP)\) 是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
二、 基本思路
我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
可在一定程度上理解为递推。
三、 几个性质
- 子问题重叠性:DP算法把原问题视作若干个重叠子问题的逐层递进,每个子问题的求解过程都构成一个“阶段”。在完成前一个阶段的计算后,DP才会执行下一阶段的计算。
就是通常理解的由 \(i-1\) 转化为 \(i\) 。
- 无后效性:为了保证DP中每一阶段的计算能够按顺序、不重复的进行,DP要求已经求解的子问题不受后续阶段的影响。
\(\mathcal{Future \ \ never \ \ has \ \ to \ \ do \ \ with \ \ past \ \ time \ \ ,but \ \ present \ \ does}.\)
\(\text{现在决定未来,未来与过去无关。}\)
- 最优子结构性质:可以从子问题的最优结果推出更大规模问题的最优结果。
\(e.g.\) 假设学校有 10 个班,已经计算出了每个班的最高考试成绩。那么现在要求全校最高的成绩。我们不用重新遍历全校学生的分数进行比较,而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩。
- 总结:
DP三要素:状态、阶段、决策;
DP基本条件:问题重叠性、无后效性、最优子结构性质
Part 1 - 线性DP
一、 概述
线性动态规划,是较常见的一类动态规划问题,其是在线性结构上进行状态转移,这类问题不像背包问题、区间DP等有固定的模板。
线性动态规划的目标函数( 即 \(f(i)\) )为特定变量( 即\(i\) )的线性函数,约束是这些变量的线性不等式或等式,目的是求目标函数的最大值或最小值(如经典的\(LIS\) , \(LCS\) , \(LCIS\) 等问题)。
二、 例题详解
T1 最长上升子序列(LIS)
注:子序列元素可以不相邻。
1. \(n^2\) 做法
解析:首先,我们知道每个元素本身即为一个上升序列。所以我们可以考虑 \(f[i]\) 表示以第 \(i\) 个元素为结尾的最长不上升子序列。最终结果为 \(max(f[i])\) 。状态转移方程为:
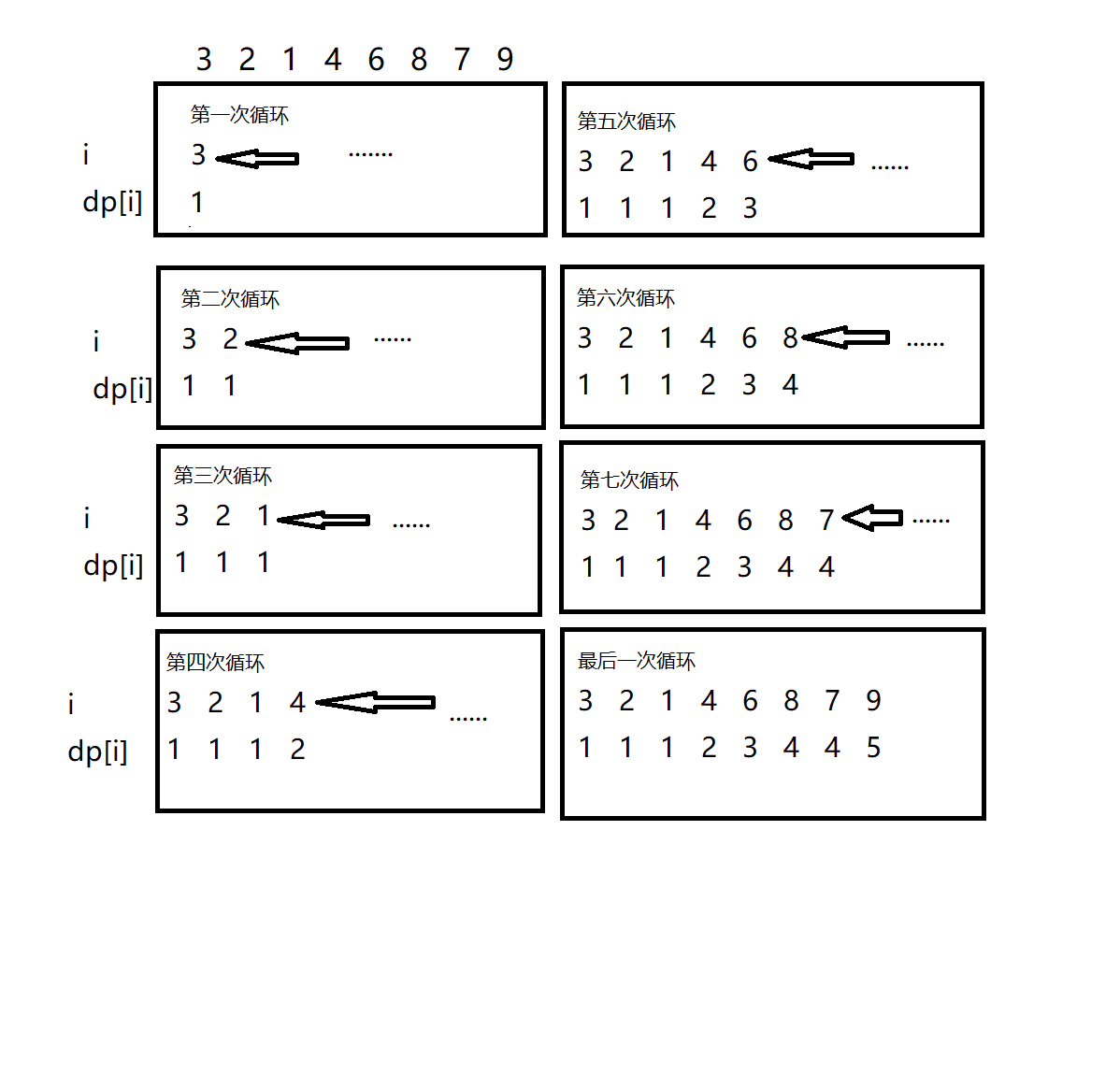
for(int i=1;i<=n;i++)
{
dp[i]=1;//初始化
for(int j=1;j<i;j++)//枚举i之前的每一个j
if(data[j]<data[i])
//用if判断是否可以拼凑成上升子序列,
//并且判断当前状态是否优于之前枚举
//过的所有状态,如果是,则↓
dp[i]=max(dp[i],dp[j]+1);//更新最优状态
//若不能,则↓
else dp[i]=max(dp[i],dp[j]);
}
2. \(nlogn\) 二分优化
我们其实不难看出,对于 \(n^2\) 做法而言,其实就是暴力枚举,数据一到 \(1e4\) 就差不多挂了...
所以考虑优化一下思路:将原来的dp数组的存储由数值换成该序列中,上升子序列长度为i的上升子序列,的最小末尾数值。
于是,这其实就是一种几近贪心的思想:我们当前的上升子序列长度如果已经确定,那么如果这种长度的子序列的结尾元素越小,后面的元素就可以更方便地加入到这条我们臆测的、可作为结果、的上升子序列中。
就是结尾元素越小,后面加入其它元素的可能性越大。
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
f[i]=0x7fffffff;
//初始值要设为INF
/*原因很简单,每遇到一个新的元素时,就跟已经记录的f数组当前所记录的最长
上升子序列的末尾元素相比较:如果小于此元素,那么就不断向前找,直到找到
一个刚好比它大的元素,替换;反之如果大于,么填到末尾元素的下一个q,INF
就是为了方便向后替换啊!*/
}
f[1]=a[1];
int len=1;//通过记录f数组的有效位数,求得个数
/*因为上文中所提到我们有可能要不断向前寻找,
所以可以采用二分查找的策略,这便是将时间复杂
度降成nlogn级别的关键因素。*/
for(int i=2;i<=n;i++)
{
int l=0,r=len,mid;
if(a[i]>f[len])f[++len]=a[i];
//如果刚好大于末尾,暂时向后顺次填充
else
{
while(l<r)
{
mid=(l+r)/2;
if(f[mid]>a[i])r=mid;
//如果仍然小于之前所记录的最小末尾,那么不断
//向前寻找(因为是最长上升子序列,所以f数组必
//然满足单调)
else l=mid+1;
}
f[l]=min(a[i],f[l]);//更新最小末尾
}
}
cout<<len;
T2 P1439 【模板】最长公共子序列(LCS)
1. \(n^2\) 做法
解析:我们可以用 \(dp[i][j]\) 来表示第一个串的前 \(i\) 位,第二个串的前 \(j\) 位的 \(LCS\) 的长度,那么我们是很容易想到状态转移方程的:
#include<iostream>
using namespace std;
int dp[1001][1001],a1[2001],a2[2001],n,m;
int main()
{
//dp[i][j]表示两个串从头开始,直到第一个串的第i位
//和第二个串的第j位最多有多少个公共子元素
cin>>n>>m;
for(int i=1;i<=n;i++)scanf("%d",&a1[i]);
for(int i=1;i<=m;i++)scanf("%d",&a2[i]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
if(a1[i]==a2[j])
dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
//因为更新,所以++; 阮行止 的博客
}
cout<<dp[n][m];
}
2. \(nlogn\) 做法
同样的,上面的算法肯定会炸...
因为洛谷此题特殊,是 \(1-n\) 的全排列,所以,我们可以通过一系列骚操作将其转化为 \(LIS\) 问题:
关于为什么可以转化成LCS问题,这里提供一个解释。
A:3 2 1 4 5
B:1 2 3 4 5
我们不妨给它们重新标个号:把3标成a,把2标成b,把1标成c……于是变成:
A: a b c d e
B: c b a d e
这样标号之后,LCS长度显然不会改变。但是出现了一个性质:
两个序列的子序列,一定是A的子序列。而A本身就是单调递增的。
因此这个子序列是单调递增的。
换句话说,只要这个子序列在B中单调递增,它就是A的子序列。
哪个最长呢?当然是B的LCS最长。
自此完成转化。
摘自阮行止 的博客
#include<iostream>
#include<cstdio>
using namespace std;
int a[100001],b[100001],map[100001],f[100001];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){scanf("%d",&a[i]);map[a[i]]=i;}
for(int i=1;i<=n;i++){scanf("%d",&b[i]);f[i]=0x7fffffff;}
int len=0;
f[0]=0;
for(int i=1;i<=n;i++)
{
int l=0,r=len,mid;
if(map[b[i]]>f[len])f[++len]=map[b[i]];
else
{
while(l<r)
{
mid=(l+r)/2;
if(f[mid]>map[b[i]])r=mid;
else l=mid+1;
}
f[l]=min(map[b[i]],f[l]);
}
}
cout<<len;
return 0
}
T3 P1020 导弹拦截
解析:本题有两问,细节巨多,可愁坏我了...
首先,对于第一问求一套系统最多能击落的导弹数,很显然我们可以求最长不上升子序列(可模仿上述 \(LIS\) 问题)。略...
其次,对于第二问求至少要多少套系统,有很多方法,你可以用最长上升子序列、贪心等...
这里只讲贪心做法:
第二问不需要知道每次如何拦截最优,只需要知道拦截多少次。
这就像一笔画问题,如果让你一笔画完成一个图案,你需要考虑怎么走。但如果给你一个一笔画完不成的图案,问你需要几笔走完,你只需要数奇点的个数就可以了。
这样做可行的原因是,所有的导弹都要拦截,用哪个导弹拦截系统都是一样的,导弹拦截系统的数目不会变。
部分代码如下:
int s=0;
len2=0;
while(s<n)
{
int maxx=0x3f3f3f3f;
for(int i=1;i<=n;i++)
if(a[i]>0&&a[i]<=maxx) s++,maxx=a[i],a[i]=-1;
len2++;
}
cout<<len2<<endl;
其它更多解法请点这里
下面在讲讲 \(STL\) 的一些做法...
三、 用 STL 实现最长不上升子序列
太多了,懒得写...\(\Rrightarrow\) 点我 \(\Lleftarrow\)
四、 线性DP的优化
- 滚动数组:如果在求解某一状态时发现其只与前一个或前几个状态有关,则可以利用滚动数组来减少空间,避免MLE。
由于滚动数组会覆盖之前的答案,所以如果只用求最终状态则建议使用滚动数组进行优化,若要求每一个状态的最优解,千万别用!!!
-
若在实现状态转移方程时遇到决策集合(指状态转移方程里的比较和选择)只增不减的情况时,可以用一个变量或数组记录,避免重复的比较,以此来降低时间复杂度。(例:LCIS 问题)
-
刷表法与填表法:
- 填表法:即普通递推...
- 刷表法:由现在的状态来推导其它状态(待补充...)
Part 2 - 写在后面
附:可能有用的题单
参考资料:
排名不分先后...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号