数据分析学习 third week （7.29~8.4）

 

概率分布简介

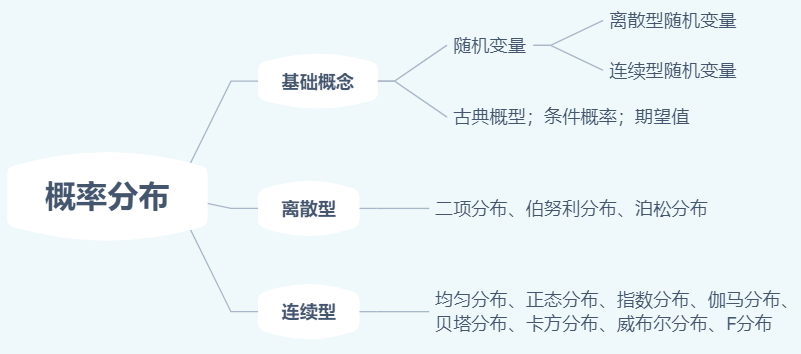
简单地介绍下常用概率分布的理论知识。 

 

基础概念

1.概率

概率直观上是指一个事件发生可能性大小的数量指标

概率的统计定义：在不变的条件下，重复进行$n$次试验，事件$A$发生的频率稳定在某一个常数$p$附近摆动，且一般来说，$n$越大，摆动幅度越小，则称常数$p$为事件$A $的概率，记作$P(A)=p$.

2.古典概型

当试验结果为有限$n$个样本点，且每个样本点的发生具有相等的可能性，如果事件A由$n_{A}$个样本点组成，则事件$A$的概率

$P(A)=\frac{n_{A}}{n}$

称有限等可能实验中事件$A $的概率$P(A)$为古典概率.

4.随机变量

定义：在样本空间$\Omega$上的实值函数$X=X(\omega), \omega \in \Omega$，称$X(\omega)$为随机变量，简记$X$.

4.1 离散型随机变量

离散型（discrete）随机变量即在一定区间内变量取值为有限个或可数个。

4.2 连续型随机变量

连续型（continuous）随机变量即在一定区间内变量取值有无限个，或数值无法一一列举出来。

定义：如果对随机变量$X$的分布函数$F(x)$，存在一个非负可积函数$f(x)$，使得对任意实数$x$，都有

$F(X)=\int_{-\infty}^{x} f(t) d t,-\infty<x<+\infty$

称$X$为连续型随机变量，函数$f(x)$称为$X$的概率密度。

4.3 期望

离散型

如果$X$是离散随机变量，具有概率质量函数$p(x)$，那么X的期望值定义为$E(X)=\sum_{x : p(x)>0} x p(x)$。换句话说，$X$的期望是$X$可能取的值的加权平均，每个值被$X$取此值的概率所加权。

连续型

我们也可以定义连续随机变量的期望值。如果$X$是具有概率密度函数$f(x)$的连续随机变量，那么$X$的期望就定义为$E(X)=\int_{\alpha}^{\beta} \frac{x}{\beta-\alpha} d x=\frac{\beta^{2}-\alpha^{2}}{2(\beta-\alpha)}=\frac{\beta+\alpha}{2}$。换句话说，在$(\alpha, \beta)$上均匀分布的随机变量的期望值正是区间的中点。

 

常用概率分布

1.二项分布

$n$重伯努利试验

定义：把一随机试验独立重复作若干，即各次试验所联系的事件之间相互独立，且同一事件在各个实验中出现的概率相同，称为独立重复试验。

    如果每次试验只有两个结果$A$和$\overline{A}$，则称这种试验为伯努利试验。将伯努利试验独立重复$n$次，称为$n$重伯努利试验。

    设在每次试验中，概率$P(A)=p(0<p<1)$，则在$n$重伯努利试验中事件$A$发生$k$次的概率，又称为二项概率公式：$C_{n}^{k} p^{k}(1-p)^{n-k}, k=0,1,2, \cdots, n$。

二项分布

如果随机变量$X$有分布律

 $P\{X=k\}=C_{n}^{k} p^{k}(1-p)^{n-k}, k=0,1,2, \cdots, n$

其中$0<p<1，q=1-p$，则称X服从参数为$n,p$的二项分布，记作$X~B(n,p)$.

二项分布就是重复$n$次独立的伯努利试验。在$n$次伯努利试验中，若每次试验成功率$p(0<p<1)$，则在$n$次独立重复试验中成功的总次数$X$服从二项分布。

当$n=1$时，二项分布为$0-1$分布，记$B(1,p)$

期望：$E(gX)=np$，方差：$D(X)=np(1-p)$

2.泊松分布

泊松分布的概率函数为：

$P(X=k)=\frac{\lambda^{k}}{k !} e^{-\lambda}, k=0,1, \cdots$

泊松分布的参数$\lambda$是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。

泊松分布的期望和方差均为$\lambda$特征函数为$\psi(t)=\exp \left\{\lambda\left(e^{i t}-1\right)\right\}$

 

泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷数，显微镜下单位分区内的细菌分布数等等

3.均匀分布

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数$a$和$b$定义，它们是数轴上的最小值和最大值，通常缩写为$U(a，b)$.

概率密度函数：

$f(x)=\left\{\begin{array}{ll}{\frac{1}{b-a},} & {a<x<b} \\ {0} & {其他]}\end{array}\right.$

在两个边界$a$和$b$处的$f(x)$的值通常是不重要的，因为它们不改变任何$f(x) d x$的积分值。 概率密度函数有时为0，有时为$\frac{1}{b-a}$。 在傅里叶分析的概念中，可以将$f(a)$或$f(b)$的值取为$\frac{1}{2(b-a)}$，因为这种均匀函数的许多积分变换的逆变换都是函数本身。

分布函数：

$F(x)=\left\{\begin{array}{ll}{0,} & {x<a} \\ {\frac{1}{b-a},} & {a \leq x<b} \\ {1,} & {b \leq x}\end{array}\right.$

令$X_{1}, \ldots, X_{n}$是服从于$U(0,1)$的样本。 令$X(k)$为该样本的第$k$次统计量。 那么$X(k)$的概率分布是参数为$k$和$n-k+1$的β分布。期望值是：

$E\left(X_{(k)}\right)=\frac{k}{n+1}$

方差是：

$V\left(X_{(k)}\right)=\frac{k(n-k+1)}{(n+1)^{2}(n+2)}$

4.指数分布

在概率理论和统计学中，指数分布（也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟，它具有无记忆的关键性质。

随机变量$X$概率密度函数：

$f(x)=\left\{\begin{array}{ll}{\lambda e^{-\lambda x},} & {x>0} \\ {0,} & {x \leq 0}\end{array} \quad \lambda>0\right.$

设$X \sim E(\lambda)$，则$X$的分布函数：

$F(x)=\left\{\begin{array}{ll}{1-e^{-\lambda x},} & {x>0}, \\ {0,} & {x \leq 0}, \end{array} \lambda>0\right.$

期望值：$E(X)=\frac{1}{\lambda}$ 

方差：$D(X)=\operatorname{Var}(X)=\frac{1}{\lambda^{2}}$

指数分布是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等

5.正态分布

若随机变量$X$服从一个位置参数为$\mu$、尺度参数为$\sigma$的概率分布，且其概率密度函数为

$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)$

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作$X \sim N\left(\mu, \sigma^{2}\right)$，读作服从$N\left(\mu, \sigma^{2}\right)$，或$X$服从正态分布。

参数含义

正态分布有两个参数，即期望（均数）$\mu$和标准差$\sigma$，$\sigma^2$为方差。

$\mathrm{f}(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$

正态分布具有两个参数$\mu$和$\sigma^2$的连续型随机变量的分布，第一参数$\mu$是服从正态分布的随机变量的均值，第二个参数$\sigma^2$是此随机变量的方差，所以正态分布记作$\mathrm{N}(\mu, \sigma 2)$.

$\mu$是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与$\mu$邻近的值的概率大，而取离$\mu$越远的值的概率越小。正态分布以$X=\mu$为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于$\mu$。

当$\mu=0, \sigma=1$时，正态分布就成为标准正态分布

$f(x)=\frac{1}{\sqrt{2 \pi}} e^{(-\frac{x^{2}}{2} )}$

概率论中最重要的分布

正态分布有极其广泛的实际背景，生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等。一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）。从理论上看，正态分布具有很多良好的性质 ，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等

6.$\chi^{2}$分布

若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这$n$个服从标准正态分布的随机变量的平方和$Q=\sum_{i=1}^{n} \xi_{i}^{2}$构成一新的随机变量，其分布规律称为$\chi^{2}$分布（chi-square distribution），其中参数称为自由度，正如正态分布中均数或方差不同就是另一个正态分布一样，自由度不同就是另一个$\chi^{2}$分布。记为$Q\sim \chi^{2}(v)$或者$Q \sim \chi_{v}^{2}$（其中$v=n-k，k$为限制条件数）。

卡方分布是由正态分布构造而成的一个新的分布，当自由度很大时，$\chi^{2}$分布近似为正态分布。

7.Beta分布

在概率论中，贝塔分布，也称B分布，是指一组定义在$(0,1)$区间的连续概率分布，有两个参数$\alpha, \beta>0$。

B分布的概率分布函数为：

$f(x ; \alpha, \beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_{0}^{1} u^{\alpha-1}(1-u)^{\beta-1} d u}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}=\frac{1}{B(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1}$

其中$\Gamma(z)$是$\Gamma$函数。随机变量$X$服从参数为$\alpha, \beta$的Β分布通常写作$X \sim \operatorname{Be}(\alpha, \beta)$

性质：

1. 参数为$\alpha, \beta$贝塔分布的众数是：

$\frac{\alpha-1}{\alpha+\beta-2}$

2.期望值和方差分别是：

$\mu=\mathrm{E}(X)=\frac{\alpha}{\alpha+\beta}$

$\operatorname{Var}(X)=\mathrm{E}(X-\mu)^{2}=\frac{\alpha \beta}{(\alpha+\beta)^{2}(\alpha+\beta+1)}$

3.偏度是：

$\frac{\mathrm{E}(X-\mu)^{3}}{\left[\mathrm{E}(X-\mu)^{2}\right]^{3 / 2}}=\frac{2(\beta-\alpha) \sqrt{\alpha+\beta+1}}{(\alpha+\beta+2) \sqrt{\alpha \beta}}$

4.峰度是：

$\frac{\mathrm{E}(X-\mu)^{4}}{\left[\mathrm{E}(X-\mu)^{2}\right]^{2}}-3=\frac{6\left[\alpha^{3}-\alpha^{2}(2 \beta-1)+\beta^{2}(\beta+1)-2 \alpha \beta(\beta+2)\right]}{\alpha \beta(\alpha+\beta+2)(\alpha+\beta+3)}$

或：

$\frac{6\left[(\alpha-\beta)^{2}(\alpha+\beta+1)-\alpha \beta(\alpha+\beta+2)\right]}{\alpha \beta(\alpha+\beta+2)(\alpha+\beta+3)}$