Codeforces Round 1058 (Div. 1) 部分题解

Codeforces Round 1058 (Div. 1) 部分题解

镜头语言：

A. MAD Interactive Problem

先顺序询问 \([1,2,3\cdots,k]\) 如果前面都是 \(0\)，问出一个非 \(0\) 值，那这个位置的值就唯一确定了，删除这个位置继续询问。

一轮下来能问出 \(n\) 个位置的值，再反过来问一次就有另外 \(n\) 个位置的值。

第一轮需要 \(2n\) 次询问，第二轮可以忽略掉已经问出值得位置，那就只有 \(n\) 次询问。

B. Rectangles

\(n\cdot m \leq 250000\) ，那 \(\min(n,m)\leq \sqrt{250000}=500\) ，我们可以做一个 \(O(nm\cdot \min(n,m))\) 的做法。

假设 \(n<m\) ，可以枚举 \(n\) 维度的区间 \([l,r]\) ，再顺序推 \(1\) 到 \(m\) ，就能确定在 \(n\) 维度某一区间下的一些矩形，这样的复杂度是 \(O(n^2m)\) 的。

搜索到一个矩形不能暴力填充矩形（否则你就会收获一份 fst 😦 ），考虑在 \(l\) 固定时，所有的区间左端点都是 \(l\) ，这就有了一个前缀性质，可以离线下来，打一个后缀 \(\min\) ，在所有的 \(r,m\) 都搜索完成后再扫一遍后缀更新答案，复杂度就是 \(O(n^2m)\) 的。

若 \(n>m\) ，翻转 \(n,m\) 就可以。

笔者最先写的用 multiset 维护最小值，是 \(O(n^3\log n)\) 的，但卡飞了，甚至不如 \(O(n^4)\) 的暴力，multiset 是得有多慢。

C. Twin Polynomials

一个基本的观察是：\(a_i\leq n\)，否则一定不相等。

先转化成：\(i\) 向 \(a_i\) 连边形成基环树森林，每一个点 \(a_i\) 需要保证，向他连边的所有点的 \(i\) 的和恰好为 \(a_i\) 。

这里我们将 \(0\) 设为一个特殊位置，一方面 \(a_0\) 必然是不确定的，另一方面 \(i=0\) 向任何点连边不会造成任何贡献。

分析一下性质，若一个点 \(a_i\) 没有入边（叶子），则这个 \(a_i\) 必然是 \(0\) ，其连向 \(0\) 了。那也就是说，基环树上是没有树边的，全是环边（因为有树边就一定有叶子，有叶子就一定有上述情况）。

再分析一下这个环，环上每个点只有一个入边，那既然 \(i\) 向 \(a_i\) 连边，那 \(a_i=i\)，\(a_i\) 也会向 \(i\) 连边。也就是说，环长只可能是 \(2\) 或 \(1\) （自环）！

那这题就明了了，对于每个数 \(i=1,\cdots,n\) ，\(a_i\) 要不指向 \(0\) ，要不指向自己，要不找一个位置两两配对，有特殊要求 \(a_n\) 不能指向 \(0\) 。

这个是好计数的，枚举配对对数就可以了。

D1. Inverse Minimum Partition

考虑优化 1D/1D 的 DP。

可以先维护出单调栈表示以 \(r\) 为端点下，可能的最小值的位置集合。

一个性质为：要不 \(f_i=f_{i-1}\) 要不 \(f_{i}=f_{i-1}+1\) 。这启发我们单次分割区间时，不会选则太小的最小值，这样会导致区间价值过大，必然不优。

若一个区间价值大于 \(3\) ，则一定存在一个分割，分割成两个区间，价值和比原区间价值小，对于一个区间，找到其最小值 两倍以内 的最右侧位置，以这个位置分割开，左区间价值为 \(2\) 有区间，右区间价值至少砍半（因为右区间分母变成 \(2\) 倍了）。

勘误：\(f_i\) 不是单调的 （\([1,2,3,1]\)），但单调栈我们记录了 \(r\) 表示，当前的后缀最小值为 \(a_r\) ，于是我们可以按单调栈划分出若干个后缀出来，每个后缀的所有值都大于等于左端点的最小值。

若 \(a_i\geq a_{i-1}\) 则 \(f_i \geq f_{i-1}+1\) ，这是肯定的，而 \(f_i\) 能变小的原因是其找到了个中间值都比他大的区间，也就忽略掉了许多 \(a_i \geq a_{i-1}\) 的位置，这些贡献都是不优秀的，至少贡献了 \(1\) 的代价，因此此时选择 \(r\) 一定是这段区间中 \(f_j\) 最小的转移，所以是合法的。

---

---

---

• 补题：

D2. Inverse Minimum Partition

还要再挖掘点性质。

由 D1 的区间分割策略，可以发现序列答案不超过 \(2\log (a_i)\leq C=128\) 。

\(f_{l,r}\) 虽然在固定 \(l\) 时不随 \(r\) 单调，但固定 \(r\) 时是随 \(l\) 单调的：\(f_{l,r}\geq f_{l+1,r}\) ，考虑写出其转移就知道了。

这启发我们枚举 \(r\) 找到 \(128\) 个取值端点。

对于固定的 \(r\) 求 \(L_{c}\) 表示最小的 \(l\) 满足 \(f_{l,r}\leq c\) ，求出这个就完成了。

\(L_0=r+1\) ，\(L_c\) 考虑从 \(L_{c-k}\) 转移来，枚举最左侧的那段价值至多为 \(c\) 的序列，提供个转移的图：

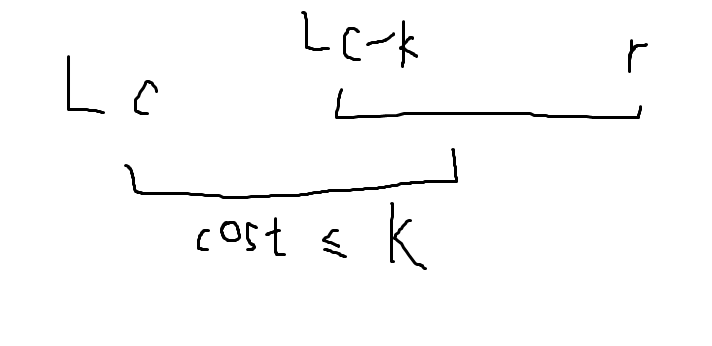
那 \(L_c=\min_k(\min_{L_{c-k}\leq i<r} Lp_{k,i})\) ，其中 \(Lp_{k,r}\) 表示以 \(r\) 为右端点，最小的左端点满足区间价值小于等于 \(k\) ，容易得出有单调性。

\(Lp\) 可以预处理出来，内部的 \(\min\) 是区间 RMQ ，再由一段区间价值最大为 \(3\) ，\(k\) 枚举到 \(3\) 就可以了。

E. Super-Short-Polynomial-San

E 很多套路，但我都不会（sad

• BSGS根号分治：\(p\) 以内的数都可以转化成 \(a\sqrt{p}-b\) 的形式，(\(a,b\leq \sqrt{p}\)) 。
• 低次多项式的幂次系数递推。

\[F^n=F^{a\sqrt{p}-b} \]

于是我们求出 \(F^{b}\) 和 \(F^{a\sqrt{p}}\) 各项系数，其中 \(a,b\leq \sqrt{p}\) ，求解一个 \(n\) 时，因为 \(F^{b}\) 次数是 \(O(\sqrt{p})\) 级别的，枚举其次数，对应于 \(F^{a\sqrt{p}}\) 的系数前缀和。

现在求 \(F^{a\sqrt{p}}\) ：更直接的，求 \(F(n)\) 表示 \(F^n\) 的系数。

神秘的转换是 \(F'(n)=(F^n(1))'=(F(n-1)\cdot F(1))'\)，前者为 \(nF'(1)F(n-1)\) 后者为 \(F'(n-1)F(1)+F(n-1)F'(1)\) 和并得到：

\[(n-1)F'(1)F(n-1)=F'(n-1)F(1) \]

两边同时提取第 \(k\) 位的系数，由 \([x^k]F'=(k+1)[x^{k+1}]F\) ，上边右式可以导出 \([x^{k+1}]F(n-1)\) ，只要将 \([x^k]\) 写开（暴力卷积计算），移项就能得到 \([x^{k+1}]F\) 的转移，由于两边都有 \(F(1)\) 相关，\(F(1)\) 的次数只有 \(2\) ，这个式子的转移就很少。

这题还卡空间，要精细划定系数范围，在计算上也要做一些优化，可以算是检验常数的一道题。

code

modInt 使用了题解的类似写法，实测 modInt 优化特别多，不清楚原理耶。