AtCoder Regular Contest 206 题解

AtCoder Regular Contest 206 题解

A - Range Replace

我们发现，若 \(a_i=a_{i+1}\) 则将操作左端点放在 \(i\) 和 \(i+1\) 是等价的，为了不重复，我们强制所有操作左端点都要放在 \(i\) 使得 \(a_i\not ={a_{i-1}}\) ，即所有值相同的连续段的最左边。

固定左端点看右端点，若 \(a_L=a_R\) ，则和操作 \((L,R-1)\) 是等价的（因为 \(a_R\) 改不改都一样），按照最小原则，这种操作我们不要。

总结一下，左端点要求 \(a_L\not ={a_{L-1}}\) ，右端点要求 \(a_L\not ={a_R}\) ，这样所有的操作得到的序列都不一样，计算这个是容易的，枚举 \(a_i\) 的值就可以了。

B - Slime Swap

冒泡排序所有的逆序对最终都需要做交换，若逆序对两位置颜色相同，则需要做更改。

澄清一个事实，假定我们选择了一些位置，这些位置做更改，则一定存在一种改颜色的方案使得最终能排好序。

因此我们要选最优的一些位置使得这些位置价值和最小。

颜色相同的位置需要考虑，枚举颜色单独拉出来，对于一个子序列，我们选择一些位置删除，使得剩余的位置单调上升（若还有逆序对则还需要更改），那很明显最优是保留 LIS 的那些位置。

于是对每个颜色，求其序列的 LIS ，就能计算答案了。

C - Tree Sequence

考虑 \(r=l+1\) 的区间。若这个区间成立则必然有 \(a_l=l+1\) 或 \(a_r=r-1\) 。

对于一个区间 \((l,l+1)\) ，若 \(a_l\not ={l+1}\) ，则必然有 \(a_{l+1}=l\) ，那再往后递进，\(a_{l+1}\not ={l+2}, a_{l+2}=l+1 \cdots\) 。

以此类推，我们发现，若某个位置有 \(a_i\not ={i+1}\) 则对于 \(x>i\) 必然有 \(a_x=x-1\) 。

那么我们尝试观察这个性质下这个序列长什么样子，最开始一段前缀，有 \(a_i=i+1\) ，直到出现一个位置 \(a_l\not ={l+1}\) ，那么往后的后缀，都有 \(a_x=x-1\) 。即，只有一个位置满足 \(a_i\not ={i+1}\) ，对于 \([1,i-1],a_x=x+1\)，对于 \([i+1,n],a_x={x-1}\) 。

那么我们枚举这个出现异常的点的位置，再判断一下前后缀是否存在方案填成这种形式，那么前后缀不造成贡献，只有这个位置造成贡献，若这个位置已经有值，则判断一下，若没有值，则任意填一个不是 \(i+1\) 的数。

注意 \(i=n\) 要特判一下。

D - LIS ∩ LDS

很坏的分讨，让大粪旋转。

对于 \(n=1\) ，只有 \(k=1\) 可以。

对于 \(n=2\) ，只有 \(k=2\) 可以。

对于 \(n > 3\) 的情况：

• \(k \geq 2\) 必然有解：
  • 构造 \(\{1,2,3,\cdots,n-k,n,n-1,n-2,\cdots,n-k+1\}\) ，LDS 为一个后缀，LIS 为前缀加 LDS 后缀的随便一个。
• \(k=1\) 在 \(n \geq 5\) 后有解：
  • 有构造 \(\{2,5,3,1,4\}\) ，更大的 \(n\) 只需要把 \(\{n,n-1,\cdots,6\}\) 插在最开头就可以。
• \(k=0\) 在 \(n \geq 8\) 后有解：
  • 有构造 \(\{3,4,8,7,2,1,5,6\}\) ，更大的 \(n\) 把 \(\{n,n-1,\cdots,9\}\) 插在最前面。

具体怎么发现的呢？挂了两发打表看出来的。

E - Rectangle Coloring

怎么又是分讨。

我们从直观上认为只要 U,D,L,R 分别取两个就可以达成情况，此时答案为各取两个最小值。

但这个是不正确的，可能中间会漏出来一个矩形：

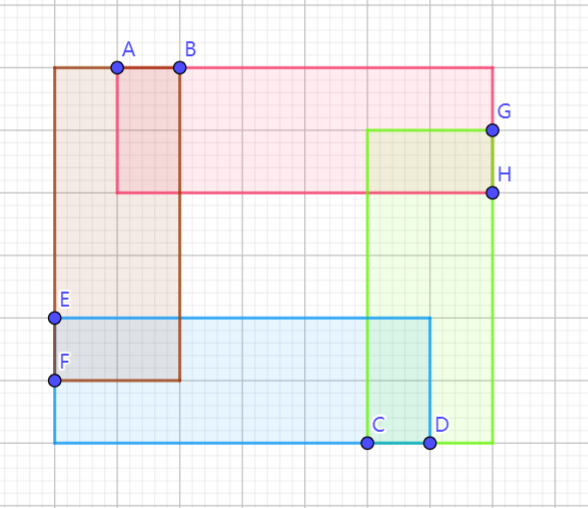
由于上下区间不挨着，且上左下右；左右区间也不挨着，左上右下（全部反过来是另一种情况）。

同时，我们发现，若此时上下再任意取一对点，即上下各 \(3\) 个，左右各 \(2\) 个，则一定存在方案（保留上边最左和下边最右，再做一次就可以），对于左右取 \(3\) 的情况是同理的，此时取点没有要求，直接选最小的几个值就可以。

以上下为例，要在每一边只取 \(2\) 个的情况下，避免上图的不合法情况，我们要求 \(3\) 个值：

1. 上区间在左，下区间在右，且两区间不交且不挨着。
2. 上下区间有至少一个交点。
3. 上区间在右，下区间在左，且两区间不交且不挨着。

具体怎么求，可以求出前缀后缀的最小值次小值，对于 2 情况，直接枚举交点，对于 1，3 情况，枚举区间挨着时的分界（例如 \([1,2],[3,4]\) 此时分界是 \(2\) 或 \(3\)）。

对于左右是同理的，我们发现在上下，左右配对时，只要不是 1 情况对 3 情况，或 3 情况对 1 情况，这组配对就是合法的。

分别对上下，左右求出 \(3\) 个值，互相配对，再考虑上下或左右选 \(3\) 对的情况，选出最小的即可。

代码

有点赤石。