Educational Codeforces Round 179 部分题解

F 在那诡辩半天，我也干了。

疑似前 \(4\) 题难度单调递减（乐。

D - Creating a Schedule

题目链接

若只有两个小组，则分别分配一个高层一个低层轮换就是最优。

多个小组，类似排序不等式那种的证明，每两个小组分配一个高低层轮换总和是最优的，就是说若 \(3\) 个小组以一种复杂的轮换关系轮换，那么选其中两个小组以最优方式轮换，答案也会更优。

按楼层排个序首末分配即可，若 \(n\) 是奇数，最后剩余的小组选剩下的一对楼层轮换就行。

E - Changing the String

题目链接

贪心策略即为从 \(1\) 到 \(n\) 尝试优先把这一位的字符变小，如果是 \(b\) 尝试变成 \(a\) ，如果是 \(c\) 尝试先变 \(a\) ，不可行就变 \(b\) 。

将 \(b\) 变成 \(a\) 有 \(b-a,b-c-a\) 两种路径，\(c\) 变 \(a\) 也有 \(c-a,c-b-c\) 两种路径，现在讨论当两种路径都存在时选哪个是更优的。

以 \(b\) 为例子，若选择了 \(b-a\) ，可能会将后续 \(c\) 的 \(c-b-a\) 路径堵掉，但剩下一个 \(c-a\) 也能让 \(c\) 一步跳到 \(a\) ；相对的若选择 \(b-c-a\) ，剩下的 \(b-a\) 不能保证后面的 \(c\) 能跳到 \(a\) （缺少 \(c-b\)），因此优先选择 \(b-a\) 是更优的，对于 \(c\) 同理。

现在考虑怎么选路径，越早出现的路径优先级越低，越晚出现的有更大机会和前面配对，因此我们的选择就是选最早出现的，对于需要配对的路径，第一步也选最早出现的，第二步再选一个后继即可。

F - Puzzle

题目链接

此题的关键在于确定充要条件。

考虑简单的构造情形，构造一个凸的图形，则该图形的周长和框住它的矩形框周长是相等的（下图）：

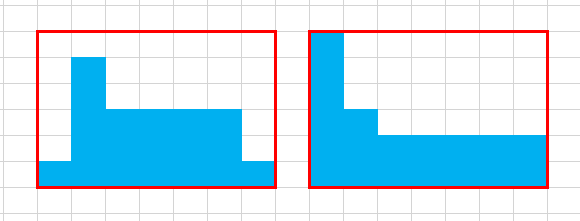
并且都能转化成右边的简易形式，也就是说我们按照某种顺序填充内部矩形框，可以在周长不变的情况下增加面积。

周长可以表示为 \(2 s\)，\(s\) 就是长和宽的和：\(s=h+w\) 。

那么在指定周长下能填的面积数在 \([h+w-1,hw]\) 之间，前者是 \(s-1\) 是定值，后者根据基本不等式，取到最大的 \(h,w\) 分别是 \(\lfloor\frac{s}{2}\rfloor,\lceil\frac{s}{2}\rceil\) ，取不同的 \(h,w\) 只有上界改变，所以可以只取最大的 \(h,w\) 覆盖其他情况。这给出了一种锁定分子只改变分母的策略。

通过枚举周长，就能用该方法构造出一些解了，现在需要说明：其他构造方法都能归约到这一种构造方法。

除了第一个方块，每次多放置/移除一个方块，都会使周长恰好改变 \(2\)，由此首先所有构造方案的周长都是偶数。

在给定的周长 \(C=2s\) 下，可以发现按照上文的简易构造需要的方块数就是最小的，并且简易构造能达到的方块书上界也是最大的（可以想象对于凹图形来说，把凹面填充满，扣掉的周长在边缘补出来）。

所以这种构造就是充要条件，只需要枚举周长的实际大小，判断方块数能否填入即可，最多填充 \(40000\) 个块，则 \(h,w\) 枚举到 \(200\) 即可。

G 在路上...