Codeforces Round 1025 部分题解

C1,C2 - Hacking Numbers

一个数能被 \(9\) 整除的条件是各个位的和是 \(9\) 的倍数，而能被 \(9\) 整除的两位数都是形如 \(ab,a+b=9 (18,27,36\cdots)\) 的数，我们对 \(x\) 乘 \(9\) 使得其被 \(9\) 整除，再执行 digit ，此时 \(x \leq 9\times 10^9\) ，其各位和不超过 \(100\) ，接着再执行一次 digit \(x\) 就能变成 \(9\) ，使用 \(4\) 次操作。

C3

C3 有点超前了，看不懂，说一下结论：

可以证明除了 \(81\) ，其他的 \(n\) 都可以在 \(3\) 次完成，\(81\) 只需要 \(2\) 次，具体的：

先乘 \(999999999\)，再 digit ，此时 \(x\) 一定是 \(81\) 。

D - D/D/D

可以看出来到一个点能走的边数是分奇偶的，一个奇数的 \(a_i\) 会使距离奇偶改变，而偶数则不会。

对于奇数/偶数而言，以偶数为例子，若能走到距离为 \(2k\) 的点，那一定能走到距离为 \(2k-2\) 的点，用 \(2\) 次操作来回走消耗掉就行，奇数同理。

那求出从 \(1\) 开始，最终走奇数条边的最大值，走偶数条边的最大值。再求出从 \(1\) 开始到各个点走奇数/偶数条边的最短路判断即可。

后者可以一遍 BFS 求出来，前者考虑所有的 \(sum-a_i\) 的方案更新最值（只丢掉一个 \(a_i\) 的方案），特殊的还要考虑 \(sum\) （所有的 \(a_i\) 都用上）的方案。

E - Binary String Wowee

如何设计状态？考虑将所有操作都在 \([i,n]\) 中的方案设为子问题，设 \(f_{i,j}\) 表示所有操作都在 \([i,n]\) 中，有 \(j\) 个操作数的方案数。

转移时枚举 \(i\) 位置操作多少次，设为 \(d\) 次，则：

\[f_{i,j}\gets f_{i+1,j-d}\times g \]

这里 \(g\) 是转移系数，表示 \(j-d\) 个操作中插入 \(d\) 个操作使操作合法的方案数，\(j-d\) 个操作中一共有 \(j-d+1\) 个空隙，若 \(s_i=1\)，则第一步操作只能插在 \(2,4,\cdots\) 的位置，即需要前面的奇数次操作使 \(s_i=0\) ，同时要保证相邻两个操作差为奇数，这表明两个操作中夹了奇数个额外的操作，加上前者的操作，保证在执行下一个操作时 \(s_i=0\) 。

那可以抽象出 \(g_{i,j}\) 为 \(i\) 个数中选 \(j\) 个数，第一个数是 \(1,3,\cdots\) 中的，相邻两数差为奇数的方案数，那：

\[f_{i,j}\gets \begin{cases} f_{i+1,j-d} \times g_{j-d,d} &, s_i=1\\ f_{i+1,j-d} \times g_{j-d+1,d} &, s_i=0 \end{cases}\]

求 \(g\) 也很好推，\(g\) 似乎就是组合数。

F - Penguin Steps

先求出瓶颈路 \(dis_M\)。

显然，\(dis_F\) 是可以二分的，对于二分值 \(mid\) ，若 \(mid \leq dis_M\) ，则问题可以转化成简单的求最小割问题。

若 \(mid > dis_M\)，我们考虑 Mouf（左上角）的一条达成 \(dis_M\) 的路径，它可以将网格分成两部分，第一部分是 Fouad（左下角）不用经过该路径就能到达的点，另一部分是必须要经过该路径才能到达的点，我们要让后一部分占用的格子越少越好，可以证明最终的最优路径只有一条。

假设存在两条最优路径，取其交集能得到更优的一条路径（上一个官方的图）。

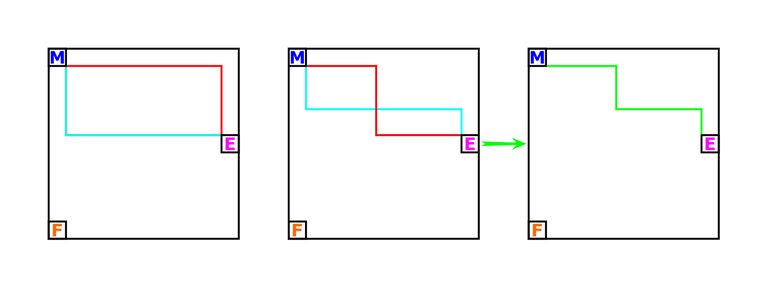
求出路径的方法可以考虑求出每一列该路径占用的格子，是个前缀（考虑上图绿色线的上半部分）。

那原问题本质上只多了个不能修改第二部分格子的限制，也是最小割。