笔记：类欧几里得

类欧几里得算法笔记

形式

类欧几里得可以在 \(O((p+q)^4\log M)\) 的复杂度内解决形如：

\[\sum_{i=0}^ni^q\lfloor\frac{Ai+B}{M}\rfloor^p \]

的问题 (\(n,M,A,B>0\))，由于其转化过程和复杂度证明和欧几里得法（辗转相除）相似，称作类欧几里得（国外喜欢称作 floor sum）。

简易形式

简易形式 \(q=0,p=1\) 令：

\[f(N,M,A,B)=\sum_{i=0}^N\lfloor\frac{Ai+B}{M}\rfloor \]

一些小性质

对于任意正实数 \(N\) ：

\[\begin{align*} x&<N \Leftrightarrow \lfloor x \rfloor <N \\ x&\leq N \Leftrightarrow \lceil x \rceil \leq N \\ x&>N \Leftrightarrow \lceil x \rceil >N \\ x&\geq N \Leftrightarrow \lfloor x \rfloor \geq N \\ \end{align*}\]

\[\lceil\frac{X}{Y}\rceil =\lfloor\frac{X+Y-1}{Y} \rfloor \]

注意，推导式子时一定要使用充要条件，例如 \(x<\lfloor N\rfloor\) 不能直接写成 \(x<N\) ，这是个必要不充分条件，会导致解集扩大。

正确做法是写成 \(x+1 \leq \lfloor N\rfloor\) 这时可以写作 \(x+1 \leq N\)

解法

\[f(N,M,A,B)=\sum_{i=0}^N\lfloor\frac{Ai+B}{M}\rfloor \]

对 \(A,B\) 做除法分解：

\[f(N,M,A,B)=\sum_{i=0}^N\lfloor\frac{(\lfloor\frac{A}{M}\rfloor M + A \bmod M)i+(\lfloor\frac{B}{M}\rfloor M + B \bmod M)}{M}\rfloor \]

打开就能得到：

\[f(N,M,A,B)=\sum_{i=0}^N \frac{N(N+1)}{2}\lfloor\frac{A}{M}\rfloor + (N+1)\lfloor\frac{B}{M}\rfloor+f(N,M,A \bmod M,B \bmod M) \]

现在 \(A,B\) 都归约到了小于 \(M\) 的值。

现在要求：

\[\sum_{i=0}^N\lfloor\frac{Ai+B}{M}\rfloor=\sum_{i=0}^N\sum_{j=0}^{\lfloor\frac{Ai+B}{M}\rfloor-1} 1 \]

这里 \(j\) 从 \(0\) 枚举保证下界相同，交换求和次序得到：

\[=\sum_{j=0}^{\lfloor\frac{AN+B}{M}\rfloor-1}\sum_{i=0}^N [j< \lfloor\frac{Ai+B}{M}\rfloor] \]

观察式子，我们理应能推出形如 \(i>\lfloor x\rfloor\) 的形式，现在求 \(x\) (注意需要使用充要条件)。

\[\begin{gather*} j< \lfloor\frac{Ai+B}{M}\rfloor \\ j+1 \leq \lfloor\frac{Ai+B}{M}\rfloor \\ jM+M \leq Ai+B\\ jM+M-B-1<Ai \\ i>\lfloor\frac{jM+M-B-1}{A}\rfloor \end{gather*}\]

这样子式子变为：

\[\begin{align*} &=\sum_{j=0}^{\lfloor\frac{AN+B}{M}\rfloor-1}\sum_{i=0}^N [i>\lfloor\frac{jM+M-B-1}{A}\rfloor] \\ &=\sum_{j=0}^{\lfloor\frac{AN+B}{M}\rfloor-1}(N-\lfloor\frac{jM+M-B-1}{A}\rfloor) \\ &=KN-f(K,A,M,M-B-1) \end{align*}\]

这里 \(K=\lfloor\frac{AN+B}{M}\rfloor-1\) ，我们发现 \(M\) 和 \(A\) 替换位置了，最开始我们已经归约到了 \(A<M\) 的情况，交换位置后可以继续执行除法分解。

这个过程本质是辗转相除的过程 (\(\gcd(A,B)=\gcd(B,A\bmod B)\))，并且换元操作是 \(O(1)\) 的，复杂度即为 \(O(\log M)\) 。

一般情况的问题可以用相同的做法推出。

万能类欧几里得

转到图像上，上式等价于一条直线下方的整点个数。

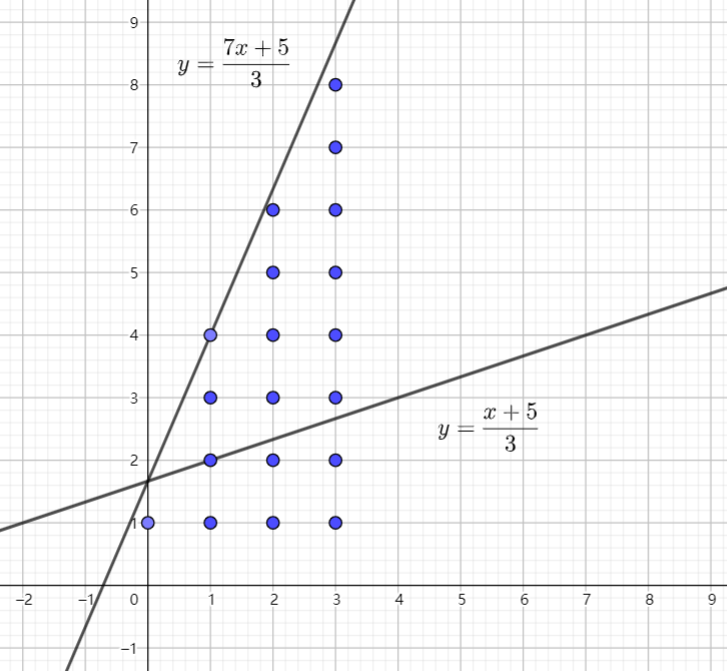
上述推式子的操作就等价于将截距取模，将斜率取模，换元操作表示将直线沿 \(y=x\) 翻转。

对于一条竖线，从 \(y=0\) 往上扫描，每碰到一条竖线，乘一个 \(R\)，每碰到一条横线，乘一个 \(U\) ，当落到整点上时先乘 \(U\) 再乘 \(R\) 。

根据矩阵递推的知识，可以创建向量 \([cnt,\sum,1]\) 表示当前线下方有多少个点，目前统计了多少个点，\(U,R\) 写成矩乘，那么我们只要求出最后整个串的矩乘就能求出答案。

上图的乘积序列就是 \([URUUURUURUUR]\) 。

那我们定义 \(f(N,A,B,M,U,R)\) 来表示这个过程。

若 \(B \geq M\) ，则序列开头是 \(\lfloor\frac{B}{M}\rfloor\) 个 \(U\)，提出来变为 \(U^{\lfloor\frac{B}{M}\rfloor}f(N,A,B\bmod M,M,U,R)\) 。

若 \(A \geq M\) ，可以缩短斜率，每个 \(R\) 前会额外附加 \(\lfloor\frac{A}{M}\rfloor\) 个 \(U\) ，变为 \(f(N,A\bmod M,B,M,U,U^{\lfloor\frac{A}{M}\rfloor}R)\) 。

当 \(A,B < M\) 时，需要交换坐标系，由 \(y \leq \lfloor\frac{Ax+B}{M}\rfloor\) 得到 \(x \geq \lfloor\frac{My-B-1}{A}\rfloor+1\) 。也就是说：第 \(x\) 个 \(R\) 前面有 \(\lfloor\frac{Ax+B}{M}\rfloor\) 个 \(U\) ，则第 \(x\) 个 \(U\) 前面有 \(\lfloor\frac{My-B-1}{A}\rfloor\) 个 \(R\) 。

这时相邻两个 \(U\) 之间 \(R\) 的个数是 \(\lfloor\frac{My-B-1}{A}\rfloor-\lfloor\frac{M(y-1)-B-1}{A}\rfloor\) ，发现 \(y=1\) 时后面式子为负数，单独拿出来做，后面的式子直接取 \(0\) ，此时从 \(x=2\) 开始是标准形式，做 \(g(x)=f(x+1)=\lfloor\frac{Mx+M-B-1}{A}\rfloor\)，上界由于平移变成 \(K-1\) ， \(K=\lfloor\frac{AN+B}{M}\rfloor\) 。

此时还有个问题，如下图：

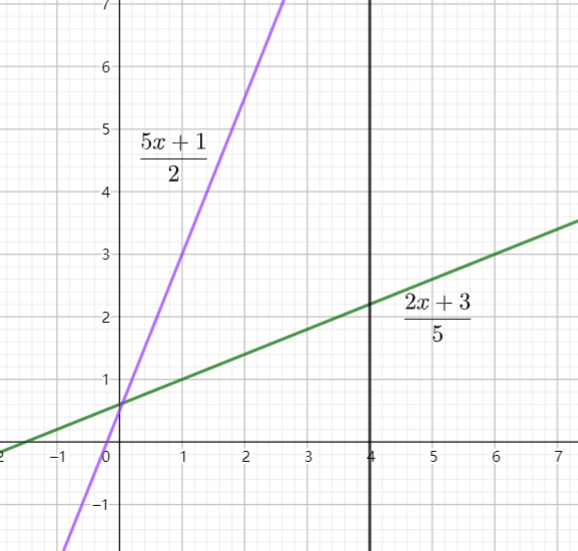
以 \(x=4\) 为界限，原始线的序列为 \(URRRUR\)，此时 \(K=2\) ，在新线上，只计算到 \(K-1=1\) 时的序列为 \(RRRU\) (注意此时 \(UR\) 交换)，加上 \(x=1\) 补上的一个 \(U\)，最后缺了一个 \(R\)，因为此时让新线内 \(y=4\) 的 \(x\) 是实数，经过下取整就会取不到。

总共需要 \(N\) 个 \(R\) ，最后还需要 \(N-\lfloor\frac{MK-B-1}{A}\rfloor\) 个 \(R\) 补充。

当 \(K=0\) 时，整条直线全是 \(R\) ，直接返回，当 \(A=0\) 时，这时不做交换，式子为 \(\lfloor\frac{B}{M}\rfloor=0\)，返回单位阵即可。

复杂度是 \(O(\log \max(A,M))\) ，快速幂相互之间可以抵消，不会证明啊。

例题

模板题

求 \(\sum y,\sum xy,\sum y^2\)

像线段树一样，万能欧几里得只需要合并两端点信息就行。

单独求 \(\sum y\) 的，比较常用，\(sum\) 是所有的和，\(cnt\) 是但前的值：

\[\begin{align*} &\sum y\\ =&\sum_Ly+\sum_R(cnty_L+y)\\ =&\sum_Ly+\sum_Ry+cnty_L\cdot cntx_R \end{align*}\]

再维护 \(cntx,cnty\) 即可。注意这里的 \(L,R\) 是对于 \(x\) 而言的。

加强模板题

求 \(\sum x^py^q\)

就是求一般形式的类欧了，考虑合并两端信息：

\[\begin{align*} &\sum x^py^q\\ =&\sum_Lx^py^q+\sum_R(x+cntx_L)^p(y+cnty_L)^q\\ =&\sum_Lx^py^q+\sum_R\sum_{k_1=0}^p\sum_{k_2=0}^q\binom{p}{k_1}\binom{q}{k_2}x^{k_1}y^{k_2}cntx_L^{p-k_1}cnty_L^{q-k_2} \\ =&\sum_Lx^py^q+\sum_Rx^{k_1}y^{k_2}\sum_{k_1=0}^p\sum_{k_2=0}^q\binom{p}{k_1}\binom{q}{k_2}cntx_L^{p-k_1}cnty_L^{q-k_2} \end{align*}\]

需要维护 \(cntx,cnty,\sum x^{k_1}y^{k_2}\) 的值，而合并一个 \(\sum x^{k_1}y^{k_2}\) 需要 \(O(k_1k_2)\) ，单次合并总复杂度是 \(O(p^2q^2)\)，比\(O((p+q)^5)\) 快。

还是模板？

给定矩阵求 \(\sum A^xB^y\) 。

合并很简单，就不推式子了。