Educational Codeforces Round 176 部分题解

D - Equalization

题意

给定整数 \(x,y\) ，一次操作选择 \(k \geq 1\)，将 \(x\) 或 \(y\) 其中一个变成 \(\lfloor\frac{a}{2^k}\rfloor\) ，代价是 \(2^k\)，每个 \(k\) 只能选一次，求让 \(x,y\) 相等的最少代价。

题解

操作就是位运算移动 \(k\) 位。

可以求出 \(f_{a,b}\) 表示将 \(x\) 移动 \(a\) 位，\(y\) 移动 \(b\) 位的最小代价，枚举这个 \(a,b\) 看 \(x,y\) 右移 \(a,b\) 位后是否相等。单次询问 \(O(\log^2 x)\) 。

代码

E - XOR Matrix

题意

给定 \(n,m,A,B\)。

求有多少对数列 \((a,b)\) 满足：

• \(a\) 的长度是 \(n\)，所有元素在 \([0,A]\) 中。

• \(b\) 的长度是 \(m\)，所有元素在 \([0,B]\) 中。

• 所有的 \(a_i \oplus b_j\) 最多只有 \(2\) 种数。

题解

一个观察是 \(a\) 或 \(b\) 中最多只有 \(2\) 种数字，否则同一个数字异或 \(3\) 个以上的不同数字必然不符合要求。

分情况讨论，有以下三种情况：

1. \(a,b\) 有 \(1\) 种数。
2. \(a,b\) 其中一个有 \(1\) 种数，其中一个有 \(2\) 种。
3. \(a,b\) 均有 \(2\) 种。

前两个很好计算，现在看第三个，设两种数分别是 \(a_1,a_2,b_1,b_2\)，要满足题目要求就有 \(a_1 \oplus b_1 = a_2 \oplus b_2\)，也可以交叉异或，是等价的。

那就可以数位 DP 了，设 \(f_{i,a_1,a_2,b_1,b_2}\) 表示第 \(i\) 位，这四个数是否分别卡在值域上限的方案数，可以把 \(4\) 个状态压缩成一个数，方便写。

最后发现使情况 \(3\) 成立的条件对情况 \(1\) 也成立，并且 DP 出来的方案数是有序的，需要改为无序。因此最终的方案数要减去情况 \(1\) 的方案数，再除以 \(4\) （\(a,b\) 都有 \(2\) 种排法）。

代码

F - Beautiful Sequence Returns

题意

一个序列是美丽的当且仅当：除了第一个数，后面的数都不是前缀最小值；除了最后一个数，前面的数都不是后缀最大值。

求一个序列的最长美丽子序列。

题解

美丽序列 \(a_n\) 的等价命题是：\(a_1<a_n\) 且 \(a_{2,3,\cdots n-1}\) 都在值域 \([a_1+1,a_n-1]\) 中。

把 \((i,a_i)\) 画到平面上，一段美丽序列可以看成一个矩形，左下角和右上角都有点，序列长度就是这个矩形除了边界上的点的数量，下面的图是个例子。

这样仍然没有优化，我们发现一个点 \((i,a_i)\) ，若它左下角也有点，则这个点必然不会作为矩形左下角端点，选其左下角的点一定是更优的。

由此，我们求出哪些点可以作为最终的左下角端点，设为 \(s_i\)。\(s_i\) 有很好的性质，它是单调不升的。对于一个不在 \(s_i\) 中的点，求出这个点在哪些候选点作左下端点时能覆盖到它，可以发现这构成 \(s_i\) 中的一个区间！

对于右上角端点，可以倒着做同样的流程，对每个非候选点也能求出一个区间。

现在我们枚举右上角端点，那么所有右上区间能覆盖到这个点的非候选点都可能被计入答案，具体在于左下端点的选择，而每个非候选点对左下端点的选择也是一个区间。我们对左下端点维护区间加减 \(1\) ，区间取 \(\max\) 的数据结构，对所有对右上角端点可行的非候选点，将其能配对的左下角端点区间加进去，查询时对这个枚举的右上端点求出哪些左下端点能构成矩形，做一个区间最大值就行。

所有的区间求解都能二分，数据结构用线段树维护即可。

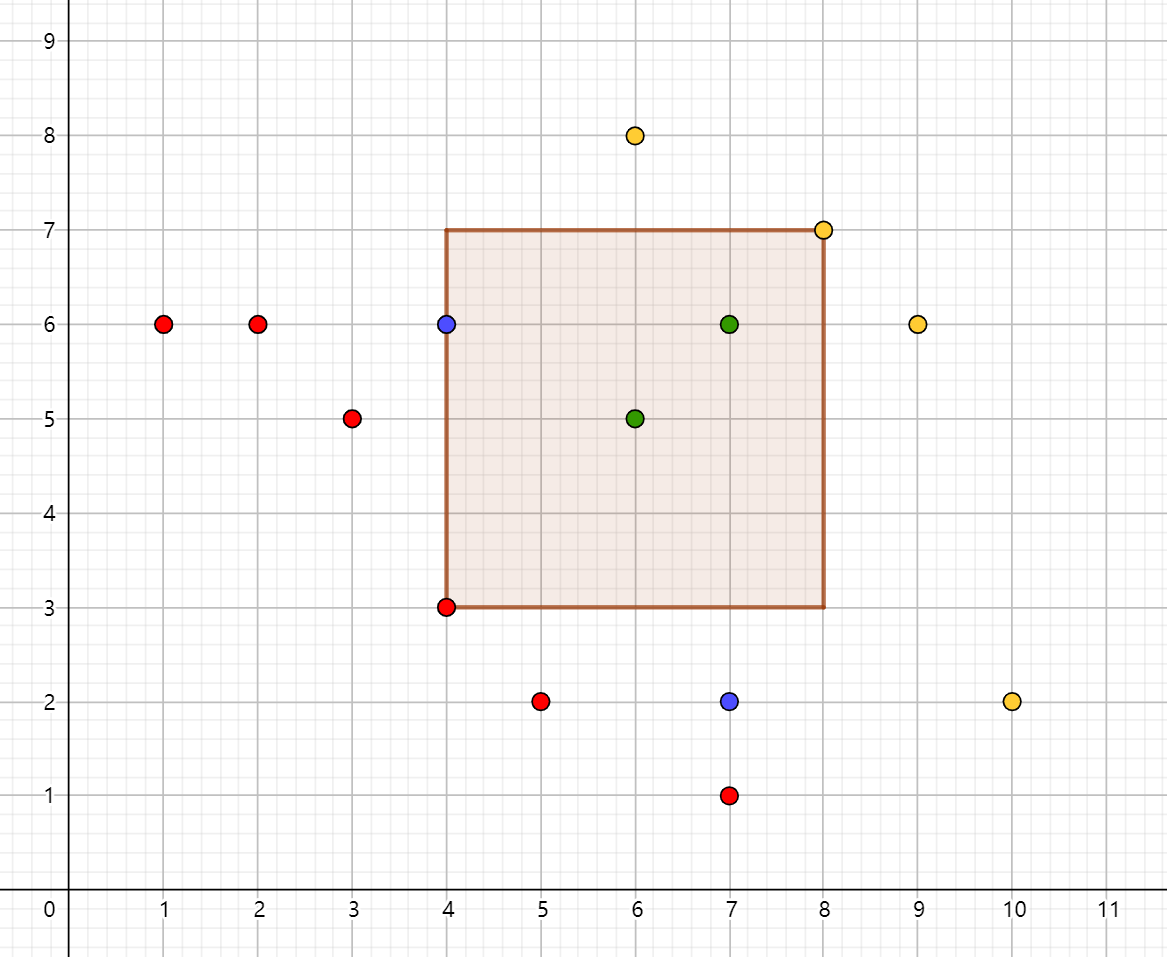
上图中，红色的点是左下端点候选点，黄色点是右上端点候选点，蓝色绿色是非候选点，在这个矩形框内，绿色的点可以被计入答案，这个矩形框的答案是 \(4\)。

这个图和题目不符，一个 \(i\) 下只有一个点，仅作参考。

注意有些右上候选点能同时成为左下候选点，需要做一些边界判断。

代码