BIT rating round ＃1 summary

BIT 校赛定段赛第一场总结

• solved 9/12，rk3 , 罚时15发（乐

历程

先拿掉 4 道签到，其中 J 题还被重边自环卡了 2 发，原本以为直接 BFS 可以忽略的。

快速扫题时，发现 G 题是做过的题，大概思路还记得，于是快快的写完首杀了（但也用了 30min）。

过完 5 题开始坐大牢， EH 题的原始题面有歧义，样例都推不出来，F 又不会做。E 题题面修正后发现从原思路转换一下就行（原思路是 \(n \times \max a_i\)），处理 \(n=3\) 处理了一大堆，前两发还漏情况了。

F 题能说的很多，这种数学题肯定有规律，于是打了个表，想要猜出来 \(n-x\) 的这个 \(x\) 什么时候最优。但规律猜错了，一直在挂，最后发现这个 \(x\) 随着 \(m\) 和 \(n\) 的差值增大会有规律的减少，但猜的规律总是对不上，总是差一些值，那就给猜出的值加了个小范围枚举，6 发罚时蒙过去（但赛后也不知道具体式子是什么）。

I 题是顺便打的，原来真会有 \(1>2,2>3,3>1\) 这种局面，诡异。

最后，H 题的题面修复了，想了半天，想到只考虑 \(0/1\) 的话，三个连续的 \(1\) 一定能一次操作搞定掉，于是从高位枚举即可。在写的时候挂了很多小细节（可以看提交记录），比如某一位有多个位置满足要求，需要打擂台，以及合并最后两个 \(1\) 时，这个位置的操作数 \(c_i\) 不能只加一，要 \(c_i=c_i+c_{i+1}+1\) （这个问题太隐蔽了，对拍好几次都拍不出来）。

D 题这种特殊图全源最短路，不会做（这种类型的都不会做），最后坐牢 2 小时。

番外：昨晚 div.1 坠机了，变紫了，特别是 C 题赛后 10min 写出来了，红温一整天！😦

部分题解

E - 小 L 的序列操作

若 \(n > 3\) ，找出最大值的位置，左边或右边一定存在长度大于 \(2\) 的区间段，即 \(\max(p-1,n-p) \geq 2\) ，将这个段操作两次变成全 \(0\) ，再结合最大值就能全部改成最大值，一边变出来后，取端点处的最大值，再把另一边也变成最大值，答案为 \(n \times \max a_i\)。

\(n=3\) 的，情况很多，暴力枚举一下。

H - 小 L 的不降序列

若 \(a_i \in \{0,1\}\)，那只要存在连续 \(3\) 个 \(1\) 就能用一次操作达成目标，否则无解。

那就可以从高位贪心，设 \(a_i\) 第 \(k\) 位组成的序列是 \(b_i,b_i \in \{0,1\}\) ，我们暴力枚举当前的一次操作是什么，把达成条件的最小操作数直接输出。

若没有位置达成条件，则 \(b_i\) 只有后 \(1\) 位或 \(2\) 位是 \(1\) ，如果只有一个 \(1\) ，那这个数就用不了了，抛弃掉。否则把最后两个 \(1\) 合并起来消掉最高位继续下一层。

因为部分位置有合并操作，我们要记录每个数被操作了多少次，设位 \(c_i\) ，合并时就 \(c_i=c_i+c_{i+1}+1\) 即可，枚举统计答案时注意也要把当前比较的每个数的 \(c_i\) 要加起来。

G - 小 L 的前后缀

把 \(t\) 翻转，操作即为交换 \(s\) 和 \(t\) 的等长前缀并翻转两个前缀。

通过操作 \([1,r]\) 和 \([1,r-1]\) 可以将 \((s_1,t_1)\) 这一对数放到 \(r\) 位置并翻转，事实上这个翻转操作没有必要，可以提前操作 \([1,1]\)。如此一来，我们可以把任意一对数放到任意位置并任意翻转。由于最终 \(t\) 还要翻转回来，于是要搞成对称的形式，统计每一对数的出现次数，对于 \(s_i \not ={t_i}\) 的对必须出现偶数对，根据 \(n\) 的奇偶性判断 \(s_i = t_i\) 的对能否出现奇数对。

D - 小 L 的最短路

这个套路打 NOI 时就考了（2023 D2T1），但忘了。

对于每个点 \(u \geq 2\) ，从 \(u\) 向 \(\lfloor\frac{u}{2}\rfloor\) 连一个虚边，构成一个二叉树。

特别的当 \(n=2^k-1\) 时是满二叉树，下图展示了 \(n=15\) 的情形（将虚边隐藏）。

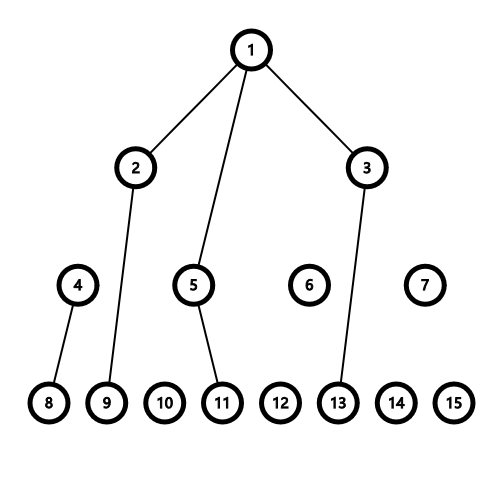
我们发现，一条边 \((u,v)\) 在原树上一定是返祖边，不存在横叉边。

对于这种深度不超过 \(\log(n)\) 的二叉树，每个点的子树大小和是不超过 \(n\log n\) 的，对于每个子树 \(u\) ，我们求解从 \(u\) 开始只经过子树内的边到达子树内的节点的最短路。

例如上述例子中当 \(u=2\) ，我们只考虑 \((2,9),(4,8),(5,11)\) 这些边。

根据所有边都是返祖边的性质，从 \(u\) 到 \(v\) 的一条路径可以表示为：\(u\) 到它的一个祖先节点 \(k\) ，再从 \(k\) 到 \(v\) (例如例子中 \(9\) 到 \(13\) 的路径)。

所以枚举 \(u,v\) 的所有公共祖先，对于祖先 \(k\) ，该路径的长度为 \(dis_{k,u}+dis_{k,v}\) ，选择最优的祖先即可。

复杂度 \(O(n\log^2 n+Q\log n)\)。