算法题——广度优先搜索

BFS访问二叉树

package cn.ganlixin.bfs;

import java.util.LinkedList;
import java.util.Queue;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class BFS {

    /**
     * 广度优先搜索，需要借助一个队列
     *
     * @param root
     */
    public static void bfs(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 根节点入队

        // 可以使用一个set标记已经走过的节点
        // Set<TreeNode> visited = new HashSet<>();

        while (!queue.isEmpty()) {
            // 元素出队
            TreeNode node = queue.poll();
            //visited.add(node); // 标记为已经处理过

            // 进行操作
            // process(node);
            System.out.print(node.val + " ");

            // 将出队元素的左右子节点依次入队
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }



    public static void main(String[] args) {
        /*
             1
           /   \
          2     3
           \   / \
            4 5   6
         */
        
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);

        root.left.right = new TreeNode(4);
        root.right.left = new TreeNode(5);
        root.right.right = new TreeNode(6);

        bfs(root); // 1 2 3 4 5 5
    }
}

　　

例题1：Catch that cow

在一个数轴上，有一个农民位于n的位置处，有一头牛位于k的位置处，农民有三种走路方式：
①若农民位于x，农民可以移动一步到x-1或x+1
②若农民位于x，农民可以跳跃到2*x处
问：农民需要最少多少步抓住那头牛？
Sample Input
5 24
100 100
Sample Output
3
0

　　

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

struct step{
    int addr;   // 当前位置
    int cnt;    //走到当前位置，走的步数
};

int start;      //农夫的起点
int target;     //奶牛的位置
bool visit[10000]; //标记某个位置是否走过。
int a[10000];   // 记录是从哪一个位置走到这个位置的，即父亲位置

//打印路径
void printPath(int cnt) {
    int parent;
    int path [cnt];
    path[cnt] = target;
    for (int i = 0; i < cnt; i++) {
        parent = a[target];
        target = parent;
        path[cnt - i - 1] = parent;
    }
    for (int i = 0; i <= cnt; i++) {
        cout << path[i] << " ";
    }
    cout << endl;
}

int bfs(step s) {
    memset(visit, false, 10000);
    memset(a, 0, 10000);
    queue<step> Q;   //一个队列
    Q.push(s);       //首先，原始位置入队
    while (!Q.empty()) {  // 队列不为空
        step cur = Q.front();  //获取队头元素
        for (int i = 0; i < 3; i++) {
            step tmp;
            if (i == 0 && cur.addr-1 > 0 && !visit[cur.addr - 1]) {
                tmp.addr = cur.addr - 1;
            } else if (i == 1 && cur.addr+1 <= 10000 && !visit[cur.addr + 1]) {
                tmp.addr = cur.addr + 1;
            } else if (i == 2 && cur.addr*2 <= 10000 && !visit[cur.addr * 2]){
                tmp.addr = cur.addr * 2;
            }
            tmp.cnt = cur.cnt + 1;   // 从当前位置到左边一个位置，步数要加1
            a[tmp.addr] = cur.addr;   // 记录器父位置
            visit[tmp.addr] = true;  // 将新位置标记为已走过
            if (cur.addr == target) {   //如果当前位置是奶牛的位置
                cout << cur.cnt << endl;  // 直接输出到当前位置所走的步数
                printPath(cur.cnt);
                return 0;
            }
            Q.push(tmp); //新入队的值不是目标节点
        }

        Q.pop();  //队首出队，因为他的下一层已经全部入队了
    }
    
    cout << "不可达" << endl;
}

int main(){
    cin >> start >> target;
    if (start == target) {
        cout << 0 << endl;
        return 0;
    }
    step s;   //农夫初始位置
    s.addr = start;
    s.cnt = 0;  // 从初始位置到初始位置的步数为0.
    visit[s.addr] = true; //将初始位置标记为走过
    bfs(s);
    return 0;
}

　　

　　

例题2：从src到dest需要几步

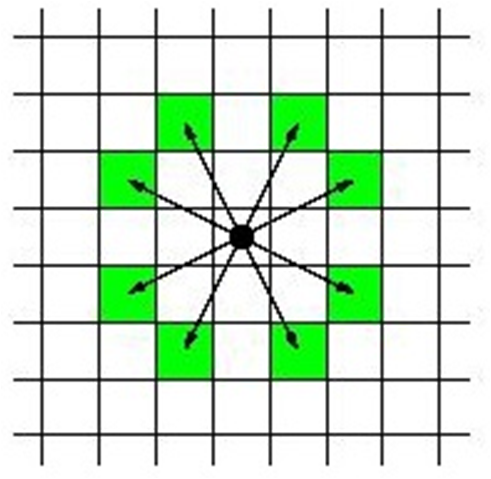
有一点处于（x1,y1）位置上，他可以向相临8个位置移动（移动方式见下图）。

划定范围：此点只可以在[0<=x<=300,0<=y<=300]范围内移动。
要求：给出起始位置(x1,y1)和目标位置(x2,y2)，要求同学求出从起始位置移动到目标位置所需的最少次数。

　　

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

struct addr{
    int x;
    int y;
    int cnt;
};

addr s; //初始位置
addr t; //目标位置
bool visit[300][300];

int bfs(addr s) {
    s.cnt = 0;
    memset(visit, false, sizeof(visit));
    visit[s.x][s.y] = true;   //将初始位置标记为已走过
    queue<addr> Q;   //一个队列
    Q.push(s);       //首先，原始位置入队
    while (!Q.empty()) {  // 队列不为空
        addr cur = Q.front();  //获取队头元素
        if (cur.x == t.x && cur.y == t.y) {   //如果当前位置是目标位置
            cout << cur.cnt << endl;  // 直接输出到大当前位置所走的步数
            return 0;
        }

        if ( (cur.x-1)>=0 && (cur.y-2)>=0 && !visit[cur.x-1][cur.y-2]) {
            addr tmp;
            tmp.x = cur.x-1;
            tmp.y = cur.y-2;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x-1][cur.y-2] = true;
            Q.push(tmp);
        }

        if ( (cur.x-2)>=0 && (cur.y-1)>=0 && !visit[cur.x-2][cur.y-1]) {
            addr tmp;
            tmp.x = cur.x-2;
            tmp.y = cur.y-1;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x-2][cur.y-1] = true;
            Q.push(tmp);
        }

        if ( (cur.x-2)>=0 && (cur.y+1)<=300 && !visit[cur.x-2][cur.y+1]) {
            addr tmp;
            tmp.x = cur.x-2;
            tmp.y = cur.y+1;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x-2][cur.y+1] = true;
            Q.push(tmp);
        }

        if ( (cur.x-1)>=0 && (cur.y+2)<=300 && !visit[cur.x-1][cur.y+2]) {
            addr tmp;
            tmp.x = cur.x-1;
            tmp.y = cur.y+2;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x-1][cur.y+2] = true;
            Q.push(tmp);
        }

        if ( (cur.x+1)<=300 && (cur.y-2)>=0 && !visit[cur.x+1][cur.y-2]) {
            addr tmp;
            tmp.x = cur.x+1;
            tmp.y = cur.y-2;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x+1][cur.y-2] = true;
            Q.push(tmp);
        }
        if ( (cur.x+2)<=300 && (cur.y-1)>=0 && !visit[cur.x+2][cur.y-1]) {
            addr tmp;
            tmp.x = cur.x+2;
            tmp.y = cur.y-1;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x+2][cur.y-1] = true;
            Q.push(tmp);
        }

        if ( (cur.x+1)<=300 && (cur.y+2)<=300 && !visit[cur.x+1][cur.y+2]) {
            addr tmp;
            tmp.x = cur.x+1;
            tmp.y = cur.y+2;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x+1][cur.y+2] = true;
            Q.push(tmp);
        }

        if ( (cur.x+2)<=300 && (cur.y+1)<=300 && !visit[cur.x+2][cur.y+1]) {
            addr tmp;
            tmp.x = cur.x+2;
            tmp.y = cur.y+1;
            tmp.cnt = cur.cnt + 1;
            visit[cur.x+2][cur.y+1] = true;
            Q.push(tmp);
        }
        Q.pop();  //队首出队，因为他的下一层已经全部入队了
    }
    return 0;
}

int main(){
    while (cin >> s.x >> s.y >> t.x >>t.y) {
        bfs(s);
    }
    return 0;
}