[树状数组]

树状数组

概念

树状数组，依旧是一个线性数组构成，但是其性质却如同树结构一样是立体的。如图所示

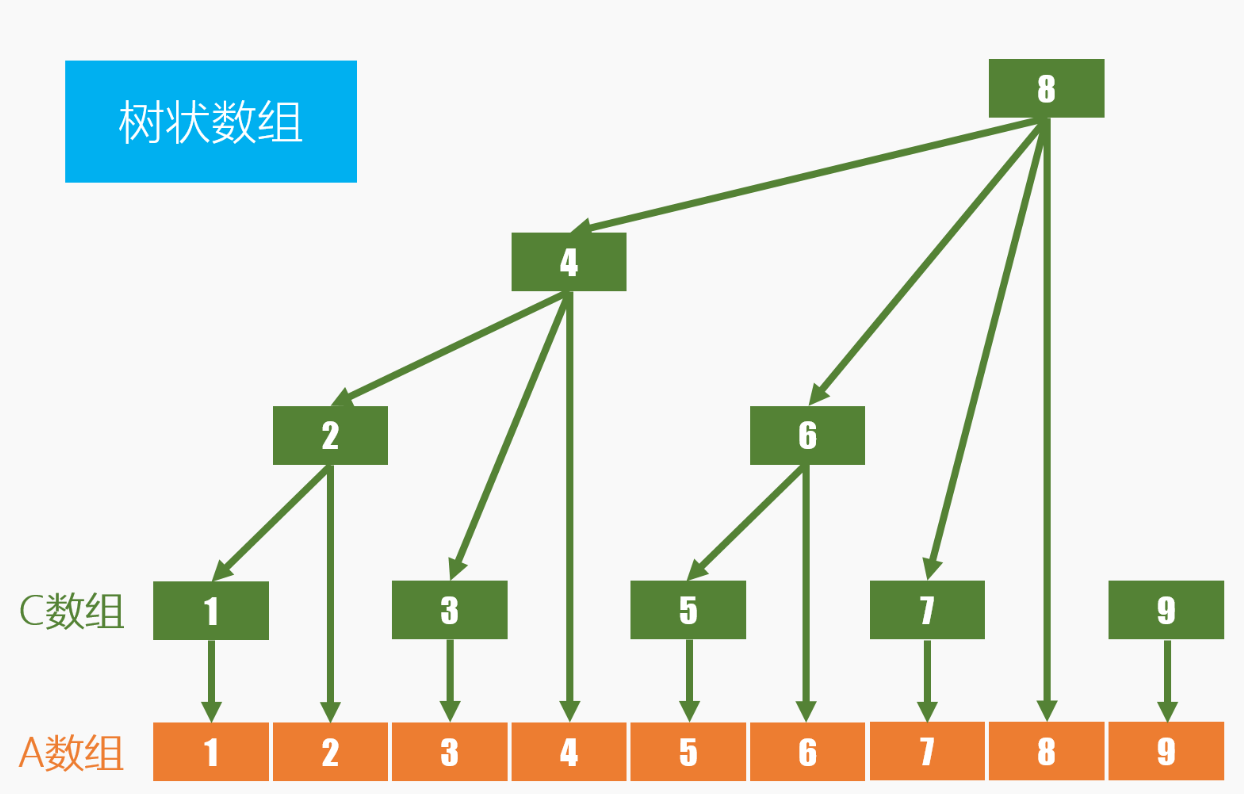
可以发现：c[1]=a[1]；c[2]=a[1]+a[2]；c[3]=a[3]；c[4]=c[2]+a[3]+a[4]=a[1]+a[2]+a[3]+a[4]；c[5]=a[5]；c[6]=a[5]+a[6]；c[7]=a[7]；c[8]=c[4]+c[6]+a[7]=a[1]+a[2]+...+a[8]。

性质

对于\(c[i]\)，他的值为从\(a[i-k+1]\)到 \(a[i]\) 的和。其中\(k\)为 \(i\)里面 2的最大次幂因子

例如，6中2的最大次幂因子为2，故 \(k=2\),\(c[6]\)的值为从\(a[5]\)到\(a[6]\)

8中2的最大次幂因子为8，故\(k=8\)，\(c[8]\)的值为从\(a[1]\)到\(a[8]\)。

构建

构建的话主要是获取\(k\)的值，而\(k\)可以通过一行代码来实现

int lowbit(int x)
{
  return x & (-x);
}

那么\(c\)数组的值就可以由这个来更新

void add(int x,int k)
{
    while(x <= n)
    {
      c[x] += k;
      x += lowbit(x);
    }
	return ;
}

查询（求和）

同理也可以用上面的方法查询

int sum(int x)
{
	int res = 0;
	while(x > 0)
	{
		res += c[x];
		x -= lowbit(x);
	}
	return res;
}

如果想要知道\([L,R]\)区间的值，就可以写\(sum(R)-sum(L-1)\)