笛卡尔树

虚假的定义:笛卡尔树，一种神奇的树，这玩意大概是一个将序列转化为一棵树的东西。首先找到序列中的最大值或者最小值，然后递归定义，找到其左边区间的最大值或最小值作为根节点的左儿子，再找到其右边区间的最大值最小值作为根节点的右儿子。
笛卡尔树可以从定义看出来，是一个类似堆的结构，满足每个结点都是子树加自己中的最小值，且满足左儿子一定在自己的左边区间，右儿子同理，也就是满足中序遍历可以得到原序列。
真正的定义:

1. 每个节点的编号满足二叉搜索树的性质。
2. 节点\(i\)的权值为 \(p_i\)，每个节点的权值满足小根堆的性质。
   优点:笛卡尔树空间非常小，只用n级别的就可以，建树也非常快，也是同一个级别。
   笛卡尔树能做什么？笛卡尔树可以将一个序列转化为树，于是RMQ(区间最值)问题，就可以转化为树上求LCA，如果假设[a,b]的LCA是x，ab一定分别在x的左右子树，否则，如果均在左子树，很容易知道x不会是LCA，假设ab在左儿子的左右子树，则左儿子才是LCA，所以ab的LCA一定在x中间[根据二叉搜索树性质 左子树都在自己的左区间，右子树都在右区间[见上文]
   而[a,b]的LCA就很容易求了，我们发现LCA上面的点，要么LCA是这个点的左儿子，要么是右儿子，总之LCA的子树一定都在上方点的左边或右边，所以说我们可以记录位置，伪代码

if(x.pos<a)如果在a左边，往右走x=rs[x];
if(x.pos>b)x=ls[x]
if(a<当前点x.pos<b){x为ab的LCA;退出不再遍历}//LCA是高度最高的，第一个在他们中间的

[求LCA应该也可以用别的方法？]
笛卡尔树还可以查区间topk
笛卡尔建树是很快的，关于建树:
放一道模板题
笛卡尔树用单调栈维护一条根往右的链，这道题是小根堆，就是维护一个下标和值都单调递增的，如果你下标大，但是你的值小，那就把那些值大的挤出去，然后插到比你小的的右子树，如果没有你就是根，你弹掉的最后一个就是你左边区间[把比你小的和其左边抛掉，根据上面的递归定义就知道，只包含这个最小值右边]，最大的，所以你的左儿子就是最后一个弹掉的

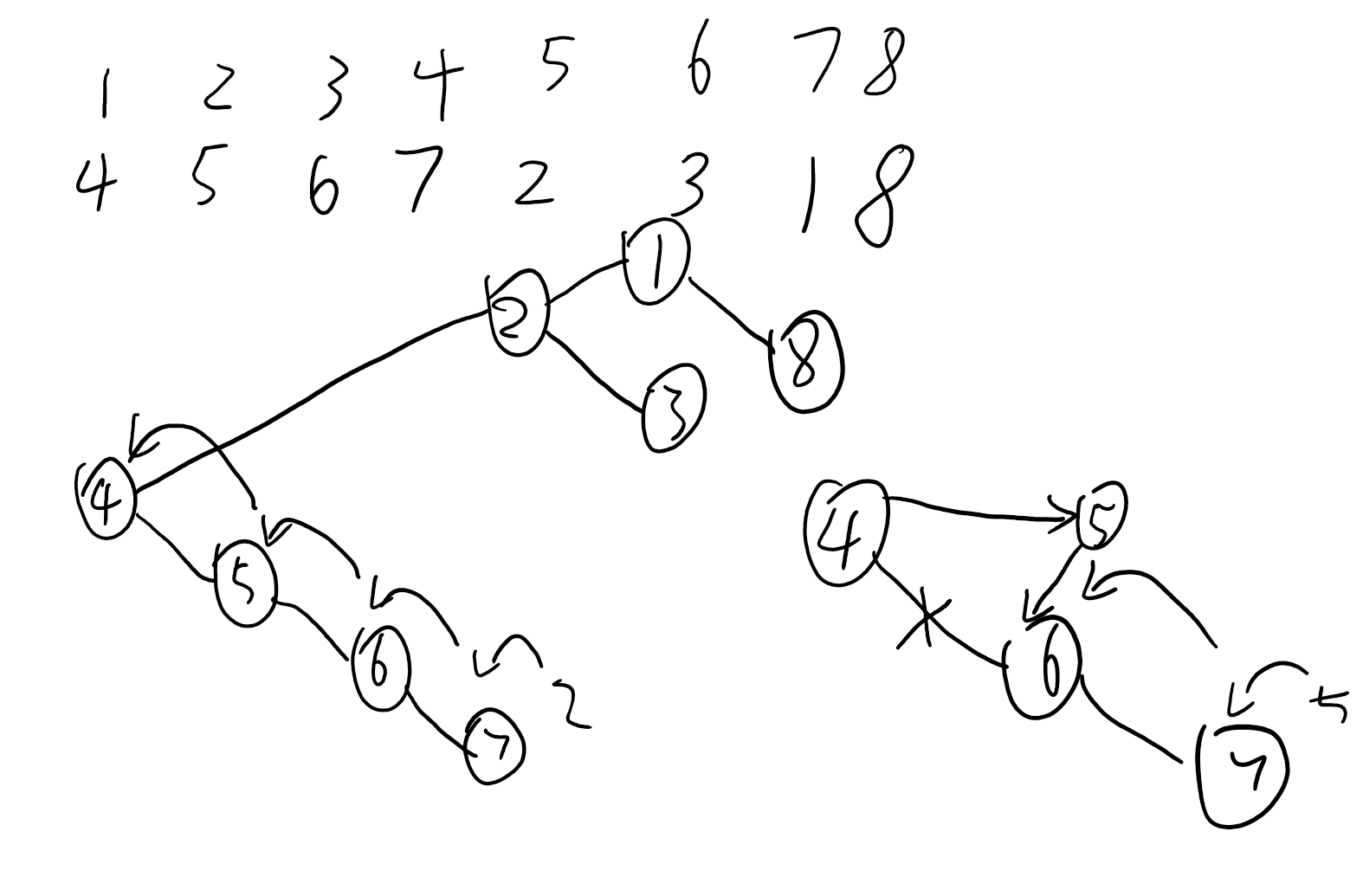
像这个图，首先把4扔进去，然后5进去，比较一下，大于4，你在4右边，并且比4小，4的右儿子是你，然后加入6，7同理，加入2的时候，2比他们都大，就弹栈到只剩下2，2发现左边没有比自己大的，即自己不会是别人的右儿子，也就是判断一下栈是否空，空了就不连，然后将自己的左儿子设成最后一个弹掉的，所以你每次维护的其实就是4 5 6 7这样一条链，如果有比他们小的，弹栈到合适位置，让比它小的给他连右儿子的边[新来的被之前的连边一定是右儿子]，它的左儿子就是上一次弹出的点[单调栈，保证这个一定是最后一个比自己大的，也就是最小的，又是顺序扫，所以一定在自己左边，所以是左儿子]
右下角那个图就是弹栈，弹栈之后更改。那个图是4 6 7 5的顺序
流程:

1. 加新点，比较和栈尾元素，比他们小[等于不等于都行，看你希望同value的时候pos小小，还是pos大小]
2. 判断栈是否为空
3. 如果为空 则当前点为新链的开头，向上一个弹出的连左儿子边 否则依然向上一个弹出的连左儿子，但同时将栈内无法弹出的最后一个元素[栈尾]向当前点连右儿子边
4. 重复上述过程
   放一下我一开始的代码吧

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+9;
int sta[N],n,ls[N],rs[N],fa[N],h=1,t=0,a[N];
long long ans1,ans2;
int read(){
    char ch;int x=0;bool flg=0;
    ch=getchar();
    while(!isdigit(ch)){if(ch=='-')flg=1;ch=getchar();}
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    return flg?-x:x;
}
void write(long long x){
    if(x<0){putchar('-');x=-x;}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
int main(){
    n=read();
    for(int i=1;i<=n;i++)a[i]=read();//你放到下面的循环，边读入边处理应该也不是什么问题 如果不用快读可能过不去luogu模板
    for(int nw,i=1;i<=n;i++){
        while(a[i]<=a[sta[t]] && h<=t){//栈不为空 且现在的值比较小 弹栈
            t--;
        }
        if(h<=t){//栈不为空
            rs[sta[t]]=i;//栈尾的右儿子是新点
            ls[i]=sta[t+1];//新点的左儿子是上一个弹出的
            fa[i]=sta[t];//新点的父亲是栈尾 其实不必记父亲？
            fa[sta[t+1]]=i;//被改变父亲的点
        }
        else{
            ls[i]=sta[t+1];//否则新点左儿子是栈尾 其实可以放外面没必要if else都写？
            fa[sta[t+1]]=i;
        }
        sta[++t]=i;//将新点下标塞到栈里
        sta[t+1]=0;//这里防止下一个点没有弹出任何点，将弹出的最后一个点重置为零，因为我们并不是真的弹栈，东西还在里面，只是我们不访问那个下标了，所以注意访问前先清空
    }
    ans1=1+ls[1];
    ans2=1+rs[1];
    for(int i=2;i<=n;i++){
        //printf("fa[%d]=%d ls=%d rs=%d\n",i,fa[i],ls[i],rs[i]);
        ans1=ans1^((1ll)*i*(ls[i]+1));
        ans2=ans2^((1ll)*i*(rs[i]+1));
    }//题目要求，记得开long long
    write(ans1);
    putchar(' ');
    write(ans2);
    return 0;
}

放一个好背诵简短的模板

for(int i=1;i<=n;i++){
        a[i]=read();//在哪里读入都可以，外面读完也行
        while(s && a[i]<=a[sta[s]]){
            l[i]=sta[s--];//栈不空且满足条件就弹栈，弹栈同时赋值，就避免了上边不弹却赋值
        }
        if(s)r[sta[s]]=i;//栈不空，栈尾元素右儿子 设为 新元素
        sta[++s]=i;//入栈
    }