实验3 C语言函数应用编程

task1

#include <stdio.h>

char score_to_grade(int score);  // 函数声明

int main() {
    int score;
    char grade;

    while(scanf("%d", &score) != EOF) {
        grade = score_to_grade(score);  // 函数调用
        printf("分数: %d, 等级: %c\n\n", score, grade);
    }

    return 0;
}

// 函数定义
char score_to_grade(int score) {
    char ans;

    switch(score/10) {
    case 10:
    case 9:   ans = 'A'; break;
    case 8:   ans = 'B'; break;
    case 7:   ans = 'C'; break;
    case 6:   ans = 'D'; break;
    default:  ans = 'E';
    }

    return ans;
}

问题1：功能是判断所给分数的等级。形参类型为整数，返回值类型为字符。

问题2：当score\10=9或者8或者7或者6时输出的答案都有误，会多出几个字符。因为没有及时break，输出结果会多。

 

task2

#include <stdio.h>

int sum_digits(int n);  // 函数声明

int main() {
    int n;
    int ans;

    while (printf("Enter n: "), scanf_s("%d", &n) != EOF) {
        ans = sum_digits(n);    // 函数调用
        printf("n = %d, ans = %d\n\n", n, ans);
    }

    return 0;
}

// 函数定义
int sum_digits(int n) {
    int ans = 0;

    while (n != 0) {
        ans += n % 10;
        n /= 10;
    }

    return ans;
}

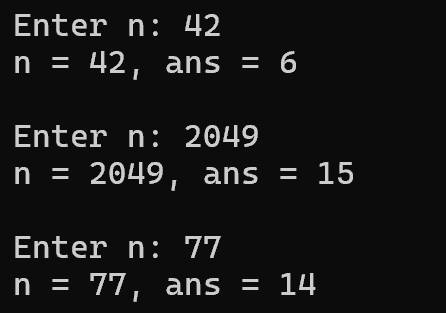
问题1：计算输入数字的各位数之和。

问题2：可以，第一种用while循环来计算每一位的值加和，第二种则是运用递归调用，将一个高阶问题转换为若干个低阶问题。

task3

#include <stdio.h>

int power(int x, int n);    // 函数声明

int main() {
    int x, n;
    int ans;

    while (printf("Enter x and n: "), scanf_s("%d%d", &x, &n) != EOF) {
        ans = power(x, n);  // 函数调用
        printf("n = %d, ans = %d\n\n", n, ans);
    }

    return 0;
}

// 函数定义
int power(int x, int n) {
    int t;

    if (n == 0)
        return 1;
    else if (n % 2)
        return x * power(x, n - 1);
    else {
        t = power(x, n / 2);
        return t * t;
    }
}

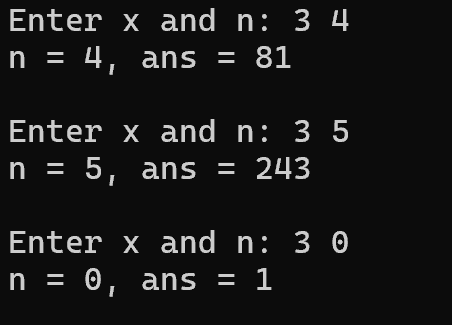
问题一：power用于计算x的n 次幂的结果

问题二：

task4

#include <stdio.h>
#include <math.h>

int is_prime(int n) {
    if (n <= 1) return 0;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            return 0;
        }
    }
    return 1;
}

int main() {
    int count = 0;
    for (int i = 3; i < 100; i++) {
        if (is_prime(i) == 1 && is_prime(i + 2) == 1) {
            printf("(%d,%d)\n", i, i + 2);
            count++;
        }
    }
    printf("总计共有%d对孪生素数\n", count);
    return 0;
}

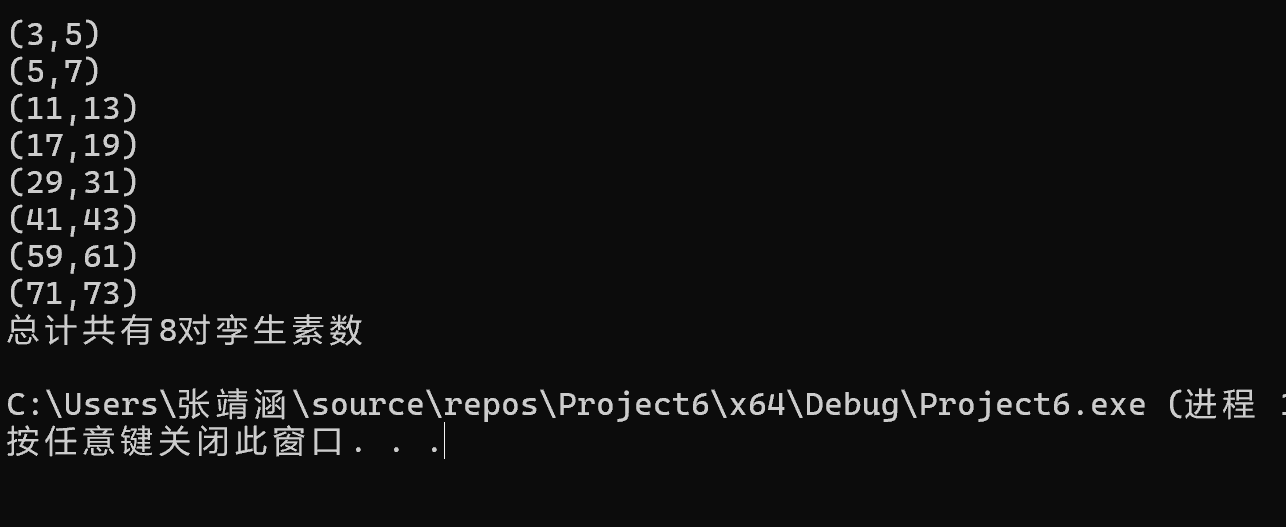
 task5

#include <stdio.h>

int move_count = 0;

void hanoi(int n, char from_rod, char to_rod, char aux_rod) {
    if (n == 1) {
        printf("1:from rod %c ---> rod %c\n", from_rod, to_rod);
        move_count++;
        return;
    }
    hanoi(n - 1, from_rod, aux_rod, to_rod);
    printf("%d: from rod %c ---> rod %c\n", n, from_rod, to_rod);
    move_count++;
    hanoi(n - 1, aux_rod, to_rod, from_rod);
}

int main() {
    int n;
    while (1) {
        printf("请输入盘子的数量 n（输入 0 退出）: ");
        if (scanf_s("%d", &n) != 1 || n == 0) {
            break;
        }
        move_count = 0;
        printf("当 n = %d 时，盘子的移动方案如下：\n", n);
        hanoi(n, 'A', 'C', 'B');
        printf("移动盘子的总次数为: %d\n\n", move_count);
    }
    return 0;
}
    

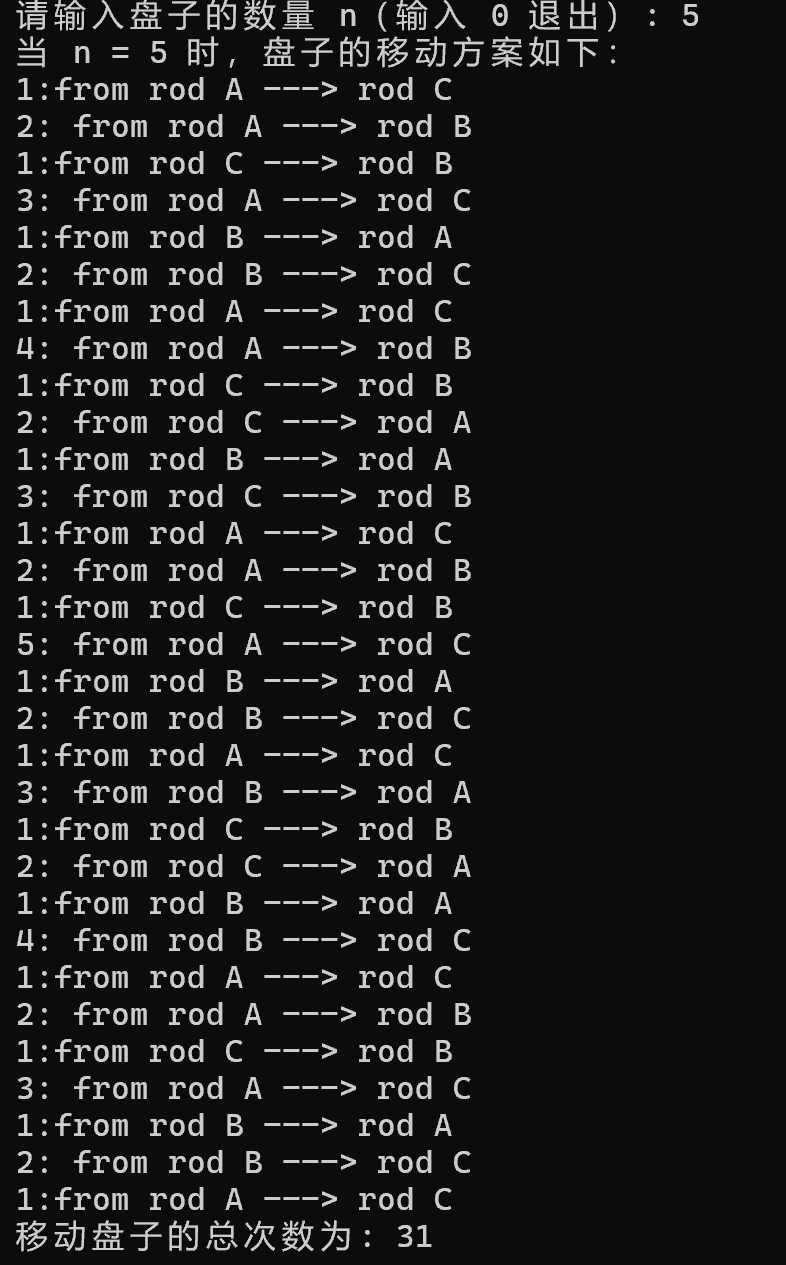
 task6

递归法

#include <stdio.h>
int func(int n, int m); // 函数声明
int main() {
    int n, m;
    int ans;
    while (scanf_s("%d%d", &n, &m) != EOF) {
        ans = func(n, m); // 函数调用
        printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
    }
    return 0;
}
int func(int n, int m)
{
    if (n == m||m==0)
        return 1;
    if (n < m)
        return 0;
    if (n>m)
    return func(n - 1, m) + func(n - 1, m - 1);


}

不太会迭代法

task7

#include <stdio.h>
// 函数声明
int gcd(int a, int b, int c);
int main() {
    int a, b, c;
    int ans;
    while (scanf_s("%d%d%d", &a, &b, &c) != EOF) {
        ans = gcd(a, b, c);
        printf("最大公约数: %d\n\n", ans);
    }
    return 0;
}
int gcd(int a, int b, int c)
{
    int min = a;
    if (b < min)
    {
        min = b;
        if (c < min)
            min = c;
    }
    int result = 1;
    // 从 2 开始到 min 逐个检查是否为公约数
    for (int i = 2; i <= min; i++) 
    {if (a % i == 0 && b % i == 0 && c % i == 0) 
            result = i;
        }
        return result;

}