关于分布

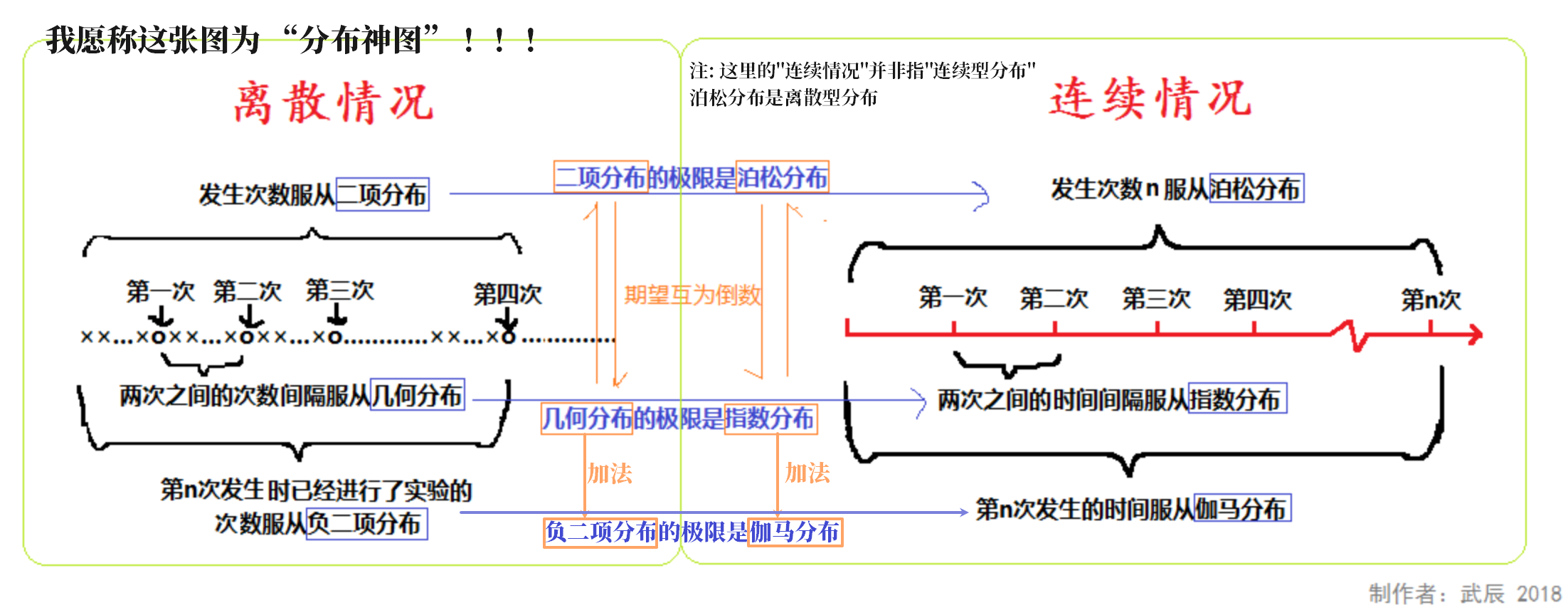
——转自 《一张图说明二项分布、泊松分布、指数分布、几何分布、负二项分布、伽玛分布的联系》

注：图片中的“连续情况”并非指“连续型随机变量”。有点“时间”的 sense？

还有一张神图：

二项分布的近似

n 大 p 不是很小, \(np \rightarrow \infty\), 实际中常用 \(np>5, nq>5\) 来作为使用正态分布来近似二项分布的条件（棣莫弗-拉普拉斯中心极限定理）

n 大 p 很小且 \(np \rightarrow \lambda\) 时可用泊松分布近似

泊松分布是在不知道事件的可能发生总次数的情况下对小概率事件建模，又叫泊松小数法则。是一个计数过程。\(\lambda>10\) 时也可用正态分布近似泊松分布（不同教材对 \(\lambda\) 大小要求不同）

根据CLT，在大样本且满足独立同分布、总体方差有限的条件下，样本均值（或样本和）的分布近似服从正态分布，无论原总体分布如何。

---

泊松分布与指数分布

这两个分布的参数 \(\lambda\) 的含义是同样的，用于衡量事件发生的频率（单位时间发生 \(\lambda\) 次）

上早八 7-8 点来的人数计算用啥分布？（np＞5） - Ans: 泊松分布、正态分布近似

指数分布拓展：指数分布相关结果

理解指数分布无记忆性的一道不错的例题。

---

几何分布与超几何分布

几何分布，对应几何级数

超几何分布，对应超几何级数

详见 知乎问答

---

分布的可加性

独立可加性定义：相互独立的 xx 分布加完之后还是 xx 分布。

具有可加性的分布：

• 泊松分布，设 \(X_1 \sim Poisson(\lambda_1), X_2 \sim Poisson(\lambda_2)\), \(X_1\) 和 \(X_2\) 相互独立，则 \(X_1+X_2 \sim Poisson(\lambda_1+\lambda_2)\).
• 伽马分布，设 \(X_1 \sim \Gamma(\alpha_1, \lambda), X_2 \sim \Gamma(\alpha_2, \lambda)\), \(X_1\) 和 \(X_2\) 相互独立，则 \(X_1+X_2 \sim \Gamma(\alpha_1+\alpha_2, \lambda)\).
• 二项分布，设 \(X_1 \sim b(n, p), X_2 \sim b(m, p)\), \(X_1\) 和 \(X_2\) 相互独立，则 \(X_1+X_2 \sim b(n+m, p)\).
• 正态分布，设 \(X \sim N(\mu_1, \sigma_1^2), Y \sim N(\mu_y, \sigma_y^2)\), \(X\) 和 \(Y\) 相互独立，则 \(aX + bY \sim N\left(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2\right)\).
• 负二项分布（r 取整数时为帕斯卡分布），设 \(X_1 \sim Nb(r_1, p), X_2 \sim Nb(r_2, p)\), \(X_1\) 和 \(X_2\) 相互独立，则 \(X_1+X_2 \sim Nb(r_1+r_2, p)\).
• 卡方分布，设 \(X_1 \sim \chi^2(n), X_2 \sim \chi^2(m)\), \(X_1\) 和 \(X_2\) 相互独立，则 \(X_1+X_2 \sim \chi^2(n+m)\).
• 柯西分布。

不具有可加性的分布：

• 0-1分布，参数 \(p\) 相同的 \(0-1\) 分布相加为二项分布，不是 \(0-1\) 分布。
• 几何分布 \(Ge(p)\), “常在河边站哪有不湿鞋”，指事件首次发生时所进行的试验次数。参数 \(p\) 相同的几何分布相加为负二项分布，不是几何分布。
• 均匀分布。
• 指数分布，\(Exp(\lambda) \sim Ga(1, \lambda)\), 参数 \(\lambda\) 相同的指数分布相加为伽马分布，不是指数分布。
• 贝塔分布。
• 超几何分布。

---

神通广大的伽马和贝塔分布 （函数）：

伽马分布：

• 伽马分布不仅可以与指数分布关联，也可与卡方分布相关联: \(Ga(\frac{n}{2}, \frac{1}{2}) \sim \chi^2(n)\).
• 若 \(X\sim Ga(\alpha, \lambda)\), 则当 \(k>0\) 时，\(kX \sim Ga(\alpha, \frac{\lambda}{k})\).

伽马函数:

• \(n \in N^+, \Gamma(n+1)=n\Gamma(n)=n!\)
• \(\Gamma(1)=0!=1, \quad \Gamma(\frac{1}{2})=\sqrt{\pi}\).

贝塔分布：

• \(Be(1, 1)=U(0, 1)\).

贝塔函数（注意不是贝塔分布）:

• \(B(a, b)=B(b, a)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}\).

---

分布的无记忆性

\(P(X>t+s|X>s)=P(X>t)\). 无记忆是指任何特定情况下的条件概率看起来就像初始的无条件概率。推导见 推文

• 指数分布。指数分布通常被称为寿命分布，灯泡 \(P(还能用5年|已经用了1年)=P(能用5年)\), 看上去很反常，但其实这里指的是“理想灯泡”，寿命足够长，只会因为其它不可控因素报废。
• 几何分布。