学习笔记——基环树

前情提要

事情是这样的，明天有个学长要来上课，老师让我们看3道题预习，某一道题中有“仙人掌”，于是跑去搜“仙人掌”，然后又扯到了“基环树”头上，于是去看基环树。

定义

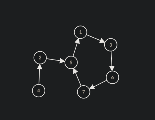
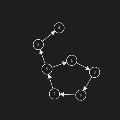
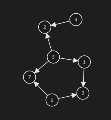
基环树的定义：一棵树添加了一条边。显然，他产生了一个环，于是便获得了一个雅号：“基环树”。
如果你不知道树是什么，再见。
特别的，若此图为有向图，还存在“内向树”与“外向树”的定义。

内向树：每个点有且只有一条出边的环。（只吃饭不拉屎）
外向树：每个点有且只有一条入边的环。（不吃饭只拉屎）

常见考法

找环

法1：拓扑排序

利用类似拓扑排序的思路。基环树删除环以后肯定会形成一片森林。森林中的每一棵树都有度为1的叶子节点.把叶子节点删除后又有了新的叶子节点。一直循环知道把森林中的每一棵树都给搞完，就只剩下了环。

#include<bits/stdc++.h>
using namespace std;
struct l{
	int x,y;
}a[100004];
int n,m,i,j,d[100004],s;
vector<int> v[100004];
queue<int> q;
int main()
{
	cin>>n;
	for(i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;
		v[a[i].x].push_back(a[i].y);
		v[a[i].y].push_back(a[i].x);
		d[a[i].x]++;
		d[a[i].y]++;
	}
	for(i=1;i<=n;i++){
		if(d[i]==1){
			q.push(i);
		}
	}
	while(q.size()){
		s=q.front();
		q.pop();
		for(i=0;i<v[s].size();i++){
			if(d[v[s][i]]>1){
				d[v[s][i]]--;
				if(d[v[s][i]]==1) q.push(v[s][i]);
			}
		}
	}
	for(i=1;i<=n;i++){
		if(d[i]==0){
			printf("%d ",i);
		}
	}
}

法2：并查集

我们按照边的顺序，将两个端点所在子树合并，如果遇到有一条边其左右两个端点已经在同一个子树中，判定为环。
然后用DFS求再从一个端点不经过此边到另一个端点的路径。

#include<bits/stdc++.h>
using namespace std;
struct l{
	int x,y;
}a[100004];
int n,m,i,j,d[100004],s,p[100004],ans[100003],b[100004];
int f(int x){
	if(x==p[x]) return x;
	return p[x]=f(p[x]);
}
vector<int> v[100004];
void dfs(int x,int y,int z){
	b[x]=1;
	if(x==z){
		for(int i=1;i<=y;i++){
			ans[i]=d[i];
//			cout<<d[i]<<" ";
		}
//		cout<<"\n";
		s=y;
		return ;
	}
    int f=1;//处理细节
	for(int i=0;i<v[x].size();i++){
		if(y==1&&v[x][i]==z&&f){//防止重边
            f=0;//有不能过过了就标记为能过
            continue;
        }
		if(b[v[x][i]]) continue;
		d[y+1]=v[x][i];
		b[v[x][i]]=1;
		dfs(v[x][i],y+1,z);
	}
}
int main()
{
	cin>>n;
	for(i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;
		v[a[i].x].push_back(a[i].y);
		v[a[i].y].push_back(a[i].x);
		p[i]=i;
	}
	for(i=1;i<=n;i++){
		if(f(a[i].x)==f(a[i].y)){
			// cout<<a[i].x<<" "<<a[i].y<<"\n";
			d[1]=a[i].x;
			dfs(a[i].x,1,a[i].y);
			break ;
		}
		p[f(a[i].x)]=f(a[i].y);
	}
	sort(ans+1,ans+1+s);
	for(i=1;i<=s;i++) cout<<ans[i]<<" ";
}

环的处理

统计环的信息

找到一个环内所有的点与环内点的数量，都可以使用并查集（别忘了有图不连通、有多个环的情况）。
例题：信息传递

#include<bits/stdc++.h>
using namespace std;
struct l{
	int x,y;
}a[200004];
int n,m,i,j,d[200004],s,ans,p[200004],z[200004];
int f(int x){
	if(p[x]==x) return x;
	return p[x]=f(p[x]);
}
vector<int> v[200004];
queue<int> q;
int main()
{
	cin>>n;
	for(i=1;i<=n;i++){
		cin>>m;
		a[i].x=i;a[i].y=m;
		v[a[i].x].push_back(a[i].y);
		v[a[i].y].push_back(a[i].x);
		d[a[i].x]++;
		d[a[i].y]++;
	}
	for(i=1;i<=n;i++){
		if(d[i]==1){
			q.push(i);
		}
	}
	// cout<<"\n";
	while(q.size()){
		s=q.front();
		q.pop();
		for(i=0;i<v[s].size();i++){
			if(d[v[s][i]]>1){
				d[v[s][i]]--;
				if(d[v[s][i]]==1) q.push(v[s][i]);
			}
		}
	}
	for(i=1;i<=n;i++){
		p[i]=i;
	}
	for(i=1;i<=n;i++){
		if(d[a[i].x]>1&&d[a[i].y]>1){
			if(f(a[i].x)==f(a[i].y)) continue;
			p[f(a[i].x)]=f(a[i].y);
		}
	}
	for(i=1;i<=n;i++){
		if(d[i]>1) z[f(i)]++;
	}
	ans=INT_MAX;
	for(i=1;i<=n;i++){
		if(d[i]>1) ans=min(ans,z[f(i)]);
	}
	cout<<ans;
}

缩环为点

#include<bits/stdc++.h>
using namespace std;
struct l{
	int x,y;
}a[100004];
int n,m,i,j,d[100004],s;
vector<int> v[100004];
queue<int> q;
int main()
{
	cin>>n;
	for(i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;
		v[a[i].x].push_back(a[i].y);
		v[a[i].y].push_back(a[i].x);
		d[a[i].x]++;
		d[a[i].y]++;
	}
	for(i=1;i<=n;i++){
		if(d[i]==1){
			q.push(i);
		}
	}
	while(q.size()){
		s=q.front();
		q.pop();
		for(i=0;i<v[s].size();i++){
			if(d[v[s][i]]>1){
				d[v[s][i]]--;
				if(d[v[s][i]]==1) q.push(v[s][i]);
			}
		}
	}
	for(i=1;i<=n;i++){
		if(d[i]==2){
			for(j=0;j<v[i].size();j++){
                v[0].push_back(v[i][j]);
                v[v[i][j]].push_back(0);
            }
		}
	}
}