图像缩放算法

1 图像缩放算法

1.1 NEAREST(最邻近插值)

缩放后某一点的像素值由缩放前和它最邻近的像素来替代。

假设我们做宽高等比例的缩放，缩放系数为 \(factor\)。原始图像的宽高分别是 \(W_{src}\) 和 \(H_{src}\)，则缩放后图像的宽高分别是 \(W_{dst}=W_{src} \times factor\) 和\(H_{dst}=H_{src} \times factor\)。
缩放后新图像某一点 \((x_{dst},y_{dst})\) 的像素值由原图像中 \((\lfloor x_{dst} \div factor \rfloor, \lfloor y_{dst} \div factor \rfloor)\) 坐标处的值代替。

1.2 LINEAR(双线性插值)

1.2.1 线性插值

假设我们想要得到一个未知的一元函数 \(f\) 在 \(x_p\) 点处的值 \(y_p\)，假设我们已知该函数 \(f\) 在 \(x_p\) 附近的两个点 \(x_1\) 和 \(x_2\) 处的值分别是 \(y_1\) 和 \(y_2\)。那么我们可以用 \([x_1,x_2]\) 范围内的一个线性函数来代替函数 \(f\) 进而求得函数 \(f\) 在点 \(x_p\) 处的值 \(y_p\)。

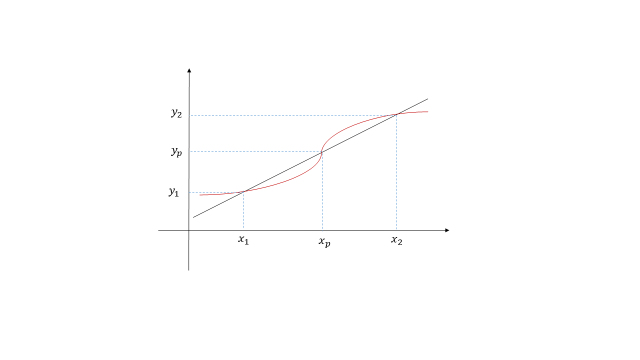
上图中的线性函数可以表示为（点斜式）：

\[y-y_1 = \frac{y_2-y_1}{x_2-x_1} (x-x_1) \]

带入点 \(x_p\) 即可近似求得 \(y_p\)。

1.2.2 双线性插值

假设我们想要得到一个未知的二元函数 \(f\) 在 \((x_p,y_p)\) 点处的值，假设我们已知该函数 \(f\) 在 \((x_p,y_p)\) 附近的四个点 \(Q_{11}=(x_1,y_1)\)、\(Q_{12}=(x_1,y_2)\)、\(Q_{21}=(x_2,y_1)\)、\(Q_{22}=(x_2,y_2)\) 处的值。首先在水平方向上进行两次线性插值得到 \(f(x_p,y_2)\) 和 \(f(x_p,y_1)\) 处的值，然后进行一次垂直方向的线性插值得到 \(f(x_p,y_p)\) 处的值。

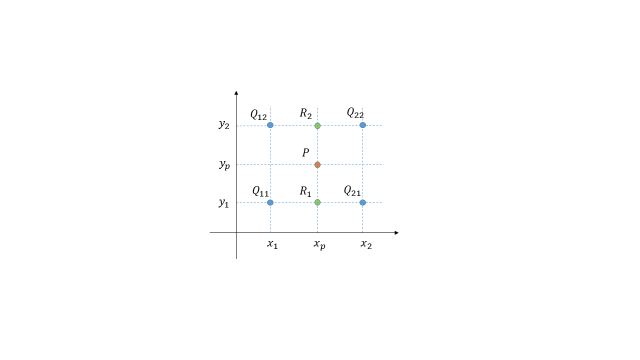
第一次水平方向插值可以看作已知点 \((x_1,f(x_1,y_1))\) 和点 \((x_2,f(x_2,y_1))\)，求点 \(f(x_p,y_1)\)：

\[f(x_p,y_1) = \frac{x_p-x_1}{x_2-x_1} f(x_2,y_1) + \frac{x_2-x_p}{x_2-x_1} f(x_1,y_1) \]

第二次水平方向插值可以看作已知点 \((x_1,f(x_1,y_2))\) 和点 \((x_2,f(x_2,y_2))\)，求点 \(f(x_p,y_2)\)：

\[f(x_p,y_2) = \frac{x_p-x_1}{x_2-x_1} f(x_2,y_2) + \frac{x_2-x_p}{x_2-x_1} f(x_1,y_2) \]

第三次垂直方向插值可以看作已知点 \((y_1,f(x_p,y_1))\) 和点 \((y_2,f(x_p,y_2))\)，求点 \(f(x_p,y_p)\):

\[\begin{align*} f(x_p, y_p) &= \frac{y_p-y_1}{y_2-y_1} f(x_p,y_2) + \frac{y_2-y}{y_2-y_1} f(x_p,y_1) \\ &= \frac{y_p-y_1}{y_2-y_1} (\frac{x_p-x_1}{x_2-x_1} f(x_2,y_2) + \frac{x_2-x_p}{x_2-x_1} f(x_1,y_2)) + \frac{y_2-y_p}{y_2-y_1} (\frac{x_p-x_1}{x_2-x_1} f(x_2,y_1) + \frac{x_2-x_p}{x_2-x_1} f(x_1,y_1)) \\ &= \frac{1}{(y_2 - y_1)(x_2 - x_1)}(f(x_2, y_2)(x_p - x_1)(y_p - y_1) + f(x_1, y_2)(x_2 - x_p)(y_p - y_1) + f(x_2,y_1)(x_p - x_1)(y_2 - y_p) + f(x_1, y_1)(x_2 - x_p)(y_2 - y_p)) \\ &= \frac{1}{(y_2 - y_1)(x_2 - x_1)} \begin{bmatrix} x_2 - x_p & x_p - x_1 \end{bmatrix} \begin{bmatrix} f(x_1,y_1) & f(x_1,y_2) \\ f(x_2,y_1) & f(x_2,y_2) \end{bmatrix} \begin{bmatrix} y_2 - y_p \\ y_p - y_1 \end{bmatrix} \end{align*} \]

通常所取的四个已知点是与 \((x_p,y_p)\) 最邻近的四个点，横纵坐标相差1个单位，因此上述公式又可以简化为：

\[ f(x_p, y_p) = \begin{bmatrix} x_2 - x_p & x_p - x_1 \end{bmatrix} \begin{bmatrix} f(x_1,y_1) & f(x_1,y_2) \\ f(x_2,y_1) & f(x_2,y_2) \end{bmatrix} \begin{bmatrix} y_2 - y_p \\ y_p - y_1 \end{bmatrix} \]

当然，先进行垂直方向的插值再进行水平方向的插值也是同样的效果。

1.2.3 双线性插值进行图像缩放

假设我们做宽高等比例的缩放，缩放系数为 \(factor\)。原始图像的宽高分别是 \(W_{src}\) 和 \(H_{src}\)，则缩放后图像的宽高分别是 \(W_{dst}=W_{src} \times factor\) 和\(H_{dst}=H_{src} \times factor\)。
缩放后新图像中某一像素点坐标 \((x_{dst},y_{dst})\) 还原到原图像中的浮点数坐标为 \((x_{dst} \div factor, y_{dst} \div factor)\)，该还原后的坐标又可以表示为 \((x_{src} + u, y_{src} + v)\) 其中 \(x_{src}\) 和 \(y_{src}\) 分别是坐标值的整数部分，\(u\) 和 \(v\) 分别是坐标值的小数部分。双线性插值所取的四个已知点坐标分别是 \((x_{src}, y_{src})\)、\((x_{src} + 1, y_{src})\)、\((x_{src}, y_{src} + 1)\)、\((x_{src} + 1, y_{src} + 1)\)。
带入到前面的双线性插值公式可以得到：

\[\begin{align*} f(x_{dst}, y_{dst}) &= f(x_{src} + u, y_{src} + v) \\ &= uv \times f((x_{src} + 1, y_{src} + 1)) + (1 - u)v \times f(x_{src}, y_{src} + 1) + u(1 - v) \times f(x_{src} + 1, y_{src}) + (1-u)(1-v) \times f(x_{src}, y_{src}) \\ &= \begin{bmatrix} 1-u & u \end{bmatrix} \begin{bmatrix} f(x_{src},y_{src}) & f(x_{src},y_{src} + 1) \\ f(x_{src} + 1,y_{src}) & f(x_{src} + 1,y_{src} + 1) \end{bmatrix} \begin{bmatrix} 1-v \\ v \end{bmatrix} \end{align*} \]

1.3 CUBIC(双三次插值)

双三次插值同样是分别在水平和垂直方向上进行插值，与双线性插值的不同在于它用三次函数来替换了双线性插值中的线性函数，并且函数 \(f\) 在点 \((x,y)\) 处的值可以由其附近网格上的16个点的值加权平均得到。双三次插值通过下面的公式计算：

\[ \begin{align*} p(x,y) &= \sum_{i=0}^3 \sum_{j=0}^3 a_{ij} x^i y^j \\ &= \begin{bmatrix} 1 & x & x^2 & x^3 \end{bmatrix} \begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \\ a_{30} & a_{31} & a_{32} & a_{33} \end{bmatrix} \begin{bmatrix} 1 & y & y^2 & y^3 \end{bmatrix} \end{align*} \]

写成矩阵乘积的形式之后，可以发现该公式与前面的双线性插值公式非常相似。

opencv中双三次插值使用的插值函数是BICUBIC函数：

\[ W(x) = \begin{cases} (a+2)|x|^3 - (a+3)|x|^2 + 1 & |x|<1 \\ a|x|^3 - 5a|x|^2 + 8a|x| - 4a & 1<|x|<2 \\ 0 & otherwise \end{cases} \]

其中的a一般取1或者-0.5，函数图像如下：

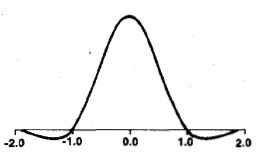
因此使用如下的插值公式：

\[ f(x,y) = \sum_{i=1}^4 \sum_{j=1}^4 f(x_i,y_j) W(x-x_i) W(y-y_j) \]

假设我们做宽高等比例的缩放，缩放系数为 \(factor\)。原始图像的宽高分别是 \(W_{src}\) 和 \(H_{src}\)，则缩放后图像的宽高分别是 \(W_{dst}=W_{src} \times factor\) 和\(H_{dst}=H_{src} \times factor\)。
缩放后新图像中某一像素点坐标 \((x_{dst},y_{dst})\) 还原到原图像中的浮点数坐标为 \(P(x_{dst} \div factor, y_{dst} \div factor)\)，该还原后的坐标又可以表示为 \(P(x_{src} + u, y_{src} + v)\) 其中 \(x_{src}\) 和 \(y_{src}\) 分别是坐标值的整数部分，\(u\) 和 \(v\) 分别是坐标值的小数部分。

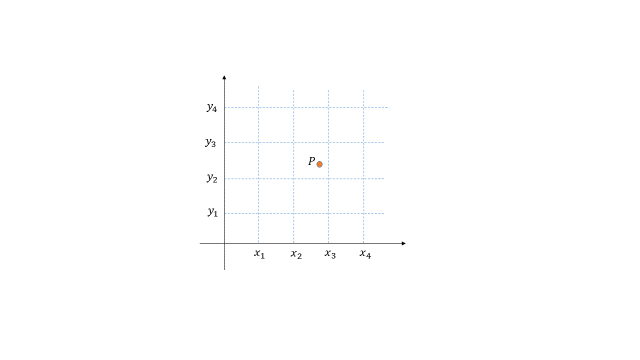
上图中的 \((x_{src},y_{src})=(x_2,y_2)\)，双三次插值的横坐标权重分别是 \(W(u+1)、W(u)、W(u-1)、W(u-2)\)，纵坐标权重分别是 \(W(v+1)、W(v)、W(v-1)、W(v-2)\)。带入数据后的插值公式如下：

\[ \begin{align*} f(x_{dst},y_{dst}) &= \sum_{i=1}^4 \sum_{j=1}^4 f(x_i,y_j) W(x_p-x_i) W(y_p-y_j) \\ &= \begin{bmatrix} W(u-2) & W(u-2) & W(u) & W(u+1) \end{bmatrix} \begin{bmatrix} f(x_1,y_1) & f(x_1,y_2) & f(x_1,y_3) & f(x_1,y_4) \\ f(x_2,y_1) & f(x_2,y_2) & f(x_2,y_3) & f(x_2,y_4) \\ f(x_3,y_1) & f(x_3,y_2) & f(x_3,y_3) & f(x_3,y_4) \\ f(x_4,y_1) & f(x_4,y_2) & f(x_4,y_3) & f(x_4,y_4) \end{bmatrix} \begin{bmatrix} W(v-2) \\ W(v-1) \\ W(v) \\ W(v+1) \end{bmatrix} \end{align*} \]

2 有参考图像质量评估方法

2.1 MSE

MSE(Mean Squared Error，均方误差)通过计算两幅图像对应像素值差的平方均值来量化误差：

\[MSE = \frac{1}{MN}\sum_{i=1}^M\sum_{j=1}^N[I_{ref}(i,j)-I_{test}(i,j)]^2 \]

MxN：图像的宽高.

\(I_{ref}, I_{test}\)：参考图像和待测图像的像素值。

优点：

1. 计算简单，数值越小，图像越相似
2. 对较大的误差敏感（平方放大了误差）。

局限性:

1. 与人类视觉不一致。忽略了人眼对亮度、纹理、局部节后的敏感度差异。
2. 依赖参考图像。需提供无失真的原始图像作为基准。
3. 忽略空间关系。仅逐像素比较，不考虑相邻像素的语义或结构信息。

2.2 PSNR

PSNR（峰值信噪比）的计算依赖于 MSE，其定义如下：

\[PSNR = 10*log_{10}(\frac{MAX_I^2}{MSE}) \]

其中 \(MAX_I\) 表示图像像素的最大可能值：

1. 对于 8 位彩色或灰度图像，\(MAX_I=255\)。
2. 对于浮点型图像（如 HDR 或某些深度模型输出），\(MAX_I\) 可能为 1.0 或其他值。

PSNR的单位是 分贝（dB），数值越大表示图像质量越好。

典型的 PSNR 范围：

1. 20~30dB：图像质量较差（有明显失真，如强压缩或噪声）。
2. 30~40dB：图像质量中等（可接受，但有一定失真）。
3. 40dB以上：图像质量较好（接近无损或轻度压缩）。
4. >50dB：基本感知无损（适用于医学成像，卫星遥感等）。

极限情况：

1. 当两幅图像完全相同时，MSE=0，PSNR 理论上趋近于无穷大（实际计算时往往设为 100dB 或其他大数替代）。
2. 当 MSE=1 时：\(PSNR=10*log_{10}(\frac{255^2}{1})\approx48.13dB\)

优点:

1. 计算简单。只需要基于均方差就可以计算。
2. 应用广泛。

局限性：

1. 与人眼感知相关性较差。PSNR只考虑像素级误差，忽略了人眼对亮度适应、纹理敏感度、边缘结构的感知特性。例如，均匀区域的轻微噪声（如天空渐变）比高频区域的同量级噪声更容易被人眼感知，但 PSNR 无法体现；结构失真（如模糊、边缘变形）可能在 PSNR 上评分较高，但视觉效果差。
2. 依赖参考图像。
3. 对异常值敏感。个别像素的极大误差会显著降低 PSNR。

2.3 SSIM

SSIM（Structural Similarity Index，结构相似性指数），是一种通过模拟人类视觉系统（HVS）的特性，更注重图像的结构信息而非像素级误差来度量两幅图像相似度的指标。

SSIM 认为人眼对图像的亮度、对比度和结构的感知是分离的，因此通过这三个分量的乘积计算相似性：

\[SSIM(x,y)=[l(x,y)]^{\alpha}*[c(x,y)]^{\beta}*[s(x,y)]^{\gamma} \]

其中：

1. x, y：待比较的两幅图像局部区域（如8x8块）
2. \(\alpha\), \(\beta\),\(\gamma\)：权重参数（通常为1）

\(SSIM\in[-1,1]\)，1表示完全相同，-1表示完全不同。

优点：

1. 与人类视觉对其。比 MSE/PSNR 更符合主观感知（尤其在模糊或压缩失真时）

局限性：

1. 计算复杂度高于 MSE/PSNR
2. 对平移、旋转等几何变化敏感（需要先对齐图像）

2.4 ffmpeg 计算质量

比较两个yuv的结构相似性（ssim）

ffmpeg -s wxh -i FilePath1 -s wxh -i FilePath2 -lavfi ssim=stats_file=ssim.txt -f null -

其中 -s 指定yuv的分辨率，FilePath 指定yuv文件路径，计算结果保存在 ssim.txt 中。

比较两个yuv的峰值信噪比（psnr）和均方差（mse）

ffmpeg -s wxh -i FilePath1 -s wxh -i FilePath2 -lavfi psnr=stats_file=psnr.txt -f null -

其中 -s 指定yuv的分辨率，FilePath 指定yuv文件路径，计算结果保存在 psnr.txt 中。

 ffmpeg -s wxh -i FilePath1 -s wxh -i FilePath2 -lavfi libvmaf=log_path=vmaf.txt -f null -