并查集
并查集相关知识的整理 :





并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
顾名思义,并查集支持两种操作:
合并(Union):合并两个元素所属集合(合并对应的树)
查询(Find):查询某个元素所属集合(查询对应的树的根节点),这可以用于判断两个元素是否属于同一集合
并查集在经过修改后可以支持单个元素的删除、移动;使用动态开点线段树还可以实现可持久化并查集.
目前所做到的题目一般操作都是路径压缩 合并 查找代表元 (启发式合并基本上没用过)
板子基本上都能手搓出来!!
//查找代表元
int findset(int x)
{
if(fa[x]==x)
return x;
return findset(fa[x]);
}
//合并
void uon(int x,int y)
{
int fx=findset(x),fy=findset(y);
if(fx==fy) return ;
fa[fx]=fy;
}
//路径压缩
int findset(int x)
{
if(x==fa[x]) return x;
fa[x]=findset(fa[x]);
return fa[x];
}
//启发式合并
void merge(int x,int y)
{
int fx=findset(x),y=findset(y);
if(fx==fy) return ;
if(sz[fx]>sz[fy]) swap(fx,fy);
fa[fx]=fy;
sz[fy]+=sz[fx];
}

这就是一个典型的判断有多少个集合 就找有多少个元素代表元等于他本身!!计数即可!! 这个没什么好讲的!!

这一个就是看起点和终点是否连通!!
我们去看点是否能走到一起 就是比较距离 若可 则合并到一个集合去 去跑一个o(n^2) 的遍历 去看是否能把两个点合并到一个集合里去 最后不就判断起点和终点的代表元是否是一个就行了
带权并查集!!!
我们还可以在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算,从而解决更多的问题。比如对于经典的「NOI2001」食物链,我们可以在边权上维护模 3 意义下的加法群。
例题 1

我们这样去看这一定是看并查集代表元最多几个 那么如何去建立并查集呢?
扩展域并查集 这些题其实也是种类并查集的一种!!!
不妨这样去建立 用x 建立 朋友集合 x+n 去建立敌人集合!!
那么 这里就要注意一定要让 x+n的代表元落在 1——n 这个范围内 这样去看多少个集合时才不会出问题那么剩下就是去合并了
注意编写代码的细节
#include <bits/stdc++.h>
using namespace std;
int n,m,ans;
int fa[4001];
int findset(int x)
{
if(x==fa[x]) return x;
fa[x]=findset(fa[x]);
return fa[x];
}
void merge(int x,int y)
{
int a=findset(x);
int b=findset(y);
fa[a]=b;
}
int main()
{
cin>>n>>m;
int i;
for(i=1;i<=2*n;i++)
fa[i]=i;
for(i=1;i<=m;i++)
{
int x,y;
char c;
cin>>c;
cin>>x>>y;
if(c=='E')
{
merge(x+n,y); //敌人的敌人是朋友!!
merge(y+n,x); //维护的敌人的集合!!
}else
{
merge(x,y);//朋友就合并呗
}
}
for(i=1;i<=n;i++)
{
if(fa[i]==i) ans++;
}
cout<<ans;
}
再来一个 一模一样的!!
https://www.luogu.com.cn/problem/P1525

这个不就是先排序 从影响力从大到小排序 先保证那些大的一定是分开的。因为只看一个,也就是实在分不开时影响力最大的那一个 所以也像团伙那样去建立带权并查集未尝不可!
但是这细分成两个监狱便有一个特殊的做法那便是记录敌人 这也是一种做法当然带权也可!
for(i=1;i<=m+1;i++)
{
if(check(a[i].x,a[i].y)) {//一直判断直到实在只能分到一个地方!!
write(a[i].z);
break;
}
else {
if(!g[a[i].x]) g[a[i].x]=a[i].y;//不存在敌人记录
else add(g[a[i].x],a[i].y);//存在敌人将敌人合并
if(!g[a[i].y]) g[a[i].y]=a[i].x;//同理
else add(g[a[i].y],a[i].x);
}
}
终极难度:食物链 这题目特别好 是一个种类并查集的典型题目!!
这里要注意是一定是分好类的也就是只有三种!!明显的分类关系

分为三种
#include <bits/stdc++.h>
using namespace std;
int fa[150001];// x+n 是吃的 x+2n 是被吃的
int findset(int x)
{
if(x==fa[x]) return x;
fa[x]=findset(fa[x]);
return fa[x];
}
void merge(int x,int y)
{
int a=findset(x);
int b=findset(y);
if(a!=b) fa[a]=b;
}
int n,k,cnt;
int main()
{
int i;
cin>>n>>k;
for(i=1;i<=3*n;i++)
{
fa[i]=i;
}
for(i=1;i<=k;i++)
{
int t,x,y;
cin>>t>>x>>y;
if(x>n||y>n) {cnt++; continue;}
if(t==1)
{
if(findset(x)==findset(y+n)||findset(x+n)==findset(y))
{ //存在敌对关系
cnt++; //假话++
}else {
merge(x,y);merge(x+n,y+n);merge(x+2*n,y+2*n);
} //把同类都合并起来
}else {
if(x==y) { 不能自己吃自己
cnt++;
continue;
}
if(findset(x)==findset(y)||findset(x)==findset(y+n))
{ //x y是同类 或者 x能吃y
cnt++;
continue;
}else {
merge(x+n,y);
merge(x+n*2,y+n);
merge(x,y+2*n);
} x+n 敌人 x+n+n 敌人的敌人 敌人的敌人吃敌人
} 1 自己 2 敌人 3敌人的敌人
1<2 2<3 3<1 这样的关系
}
cout<<cnt;
}
这里一定要注意细节的处理 : 并查集的细节 例:

这道题就是 如 x1!=x2 x2!=x3 x3!=x4 但x1=x4是没问题的
如果按照种类并查集合并的方式那么x1 x3 x4会被合并到一个集合中
1+150 2 1 2+150 2+150 3 3+150 2 很明显会出问题!
这时候不如把不相等的关系拿出来 然后先把相等的合并进去 然后最后判断有无矛盾即可
[NOI2002] 银河英雄传说
题目背景
公元 \(5801\) 年,地球居民迁至金牛座 \(\alpha\) 第二行星,在那里发表银河联邦创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。
宇宙历 \(799\) 年,银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征,气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。
题目描述
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在这次决战中,他将巴米利恩星域战场划分成 \(30000\) 列,每列依次编号为 \(1, 2,\ldots ,30000\)。之后,他把自己的战舰也依次编号为 \(1, 2, \ldots , 30000\),让第 \(i\) 号战舰处于第 \(i\) 列,形成“一字长蛇阵”,诱敌深入。这是初始阵形。当进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,实施密集攻击。合并指令为 M i j,含义为第 \(i\) 号战舰所在的整个战舰队列,作为一个整体(头在前尾在后)接至第 \(j\) 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。
然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利的第 \(i\) 号战舰与第 \(j\) 号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以及回答莱因哈特的询问。
输入格式
第一行有一个整数 \(T\)(\(1 \le T \le 5 \times 10^5\)),表示总共有 \(T\) 条指令。
以下有 \(T\) 行,每行有一条指令。指令有两种格式:
-
M i j:\(i\) 和 \(j\) 是两个整数(\(1 \le i,j \le 30000\)),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第 \(i\) 号战舰与第 \(j\) 号战舰不在同一列。 -
C i j:\(i\) 和 \(j\) 是两个整数(\(1 \le i,j \le 30000\)),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式
依次对输入的每一条指令进行分析和处理:
- 如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息。
- 如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,表示在同一列上,第 \(i\) 号战舰与第 \(j\) 号战舰之间布置的战舰数目。如果第 \(i\) 号战舰与第 \(j\) 号战舰当前不在同一列上,则输出 \(-1\)。
样例 #1
样例输入 #1
4
M 2 3
C 1 2
M 2 4
C 4 2
样例输出 #1
-1
1
提示
战舰位置图:表格中阿拉伯数字表示战舰编号
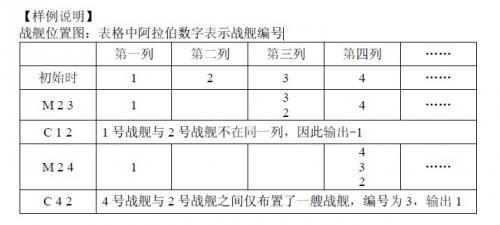
这一道题又是另一种类型的了 去维护一个并查集的队列题目特别新颖
//常用头文件!
#include <bits/stdc++.h>
using namespace std;
typedef int64_t i64;
int t;
const int mx=30005;
int fa[30005],size1[30005],front[30005];
int findset(int x) //主要就是这两个核心的函数!!!
{
if(x==fa[x]) return x;
int t=findset(fa[x]);
front[x]+=front[fa[x]]; //第x个元素前面有多少元素!!
//这样能高效处理目前队列中的各个元素前面有几个元素
return fa[x]=t;
}
void merge(int x,int y)
{
int a=findset(x);
int b=findset(y);
if(a!=b)
{
fa[a]=b;
front[a]+=size1[b];//a的前面有b那么多个元素 也就是a在b的后面
size1[b]+=size1[a];//b现在的元素
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int i,j,k;
cin>>t;
for(i=1;i<=mx;i++)
{
fa[i]=i;
size1[i]=1;
front[i]=0;
}
for(i=1;i<=t;i++)
{
char c;
int x,y;
cin>>c>>x>>y;
if(c=='M')
{
merge(x,y);
}else {
if(findset(x)!=findset(y))
{
cout<<-1<<'\n';
}else {
cout<<abs(front[x]-front[y])-1<<'\n';
输出队列相差了几个元素 -1 即为中间有多少元素!!
}
}//这道题特别特别好!!可重复做!!
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号