S6——财政收入影响因素及预测(灰色、ARIMA、支持向量回归)3136
# 数据处理
import pandas as pd
import numpy as np
# 绘图
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv(r"D:\wechat thingd\WeChat Files\k867080698\FileStorage\MsgAttach\89b755a65e2dd93c3e9546794798bf4e\File\2023-02\data.csv", encoding='gbk', index_col=0).reset_index(drop=True)
df
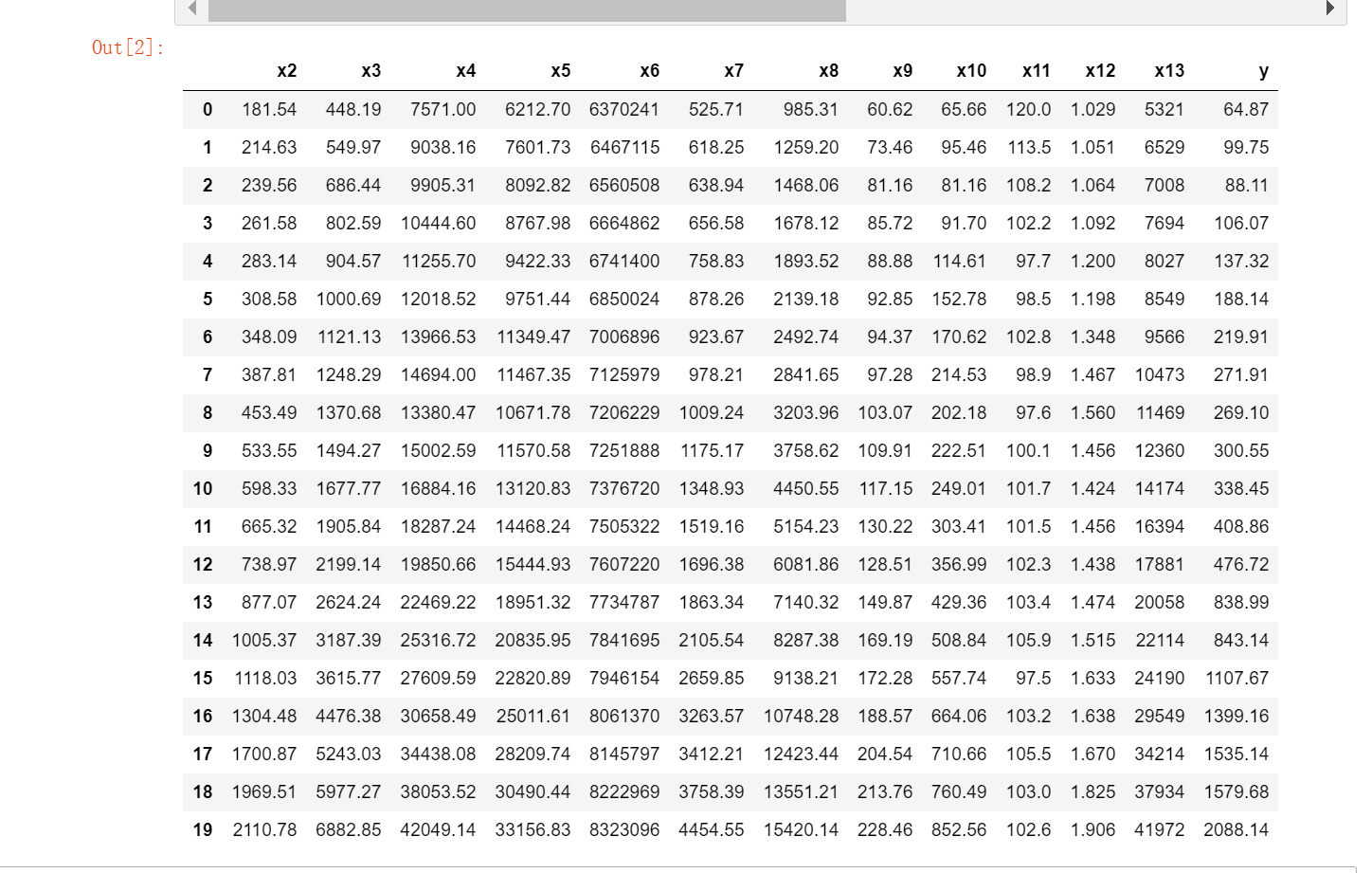
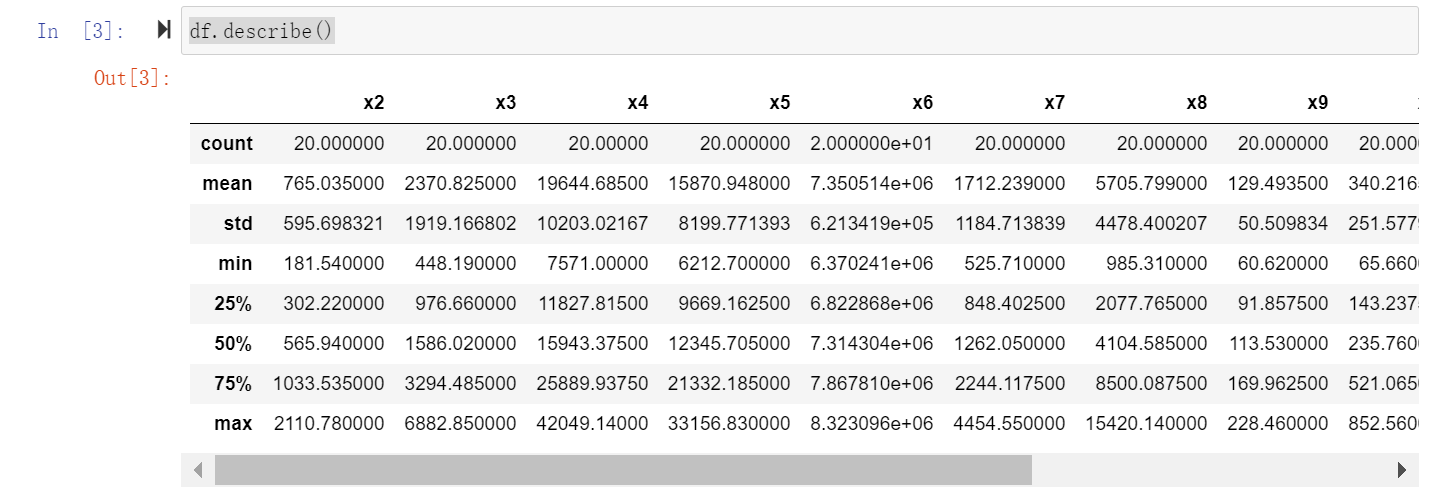
df.describe()
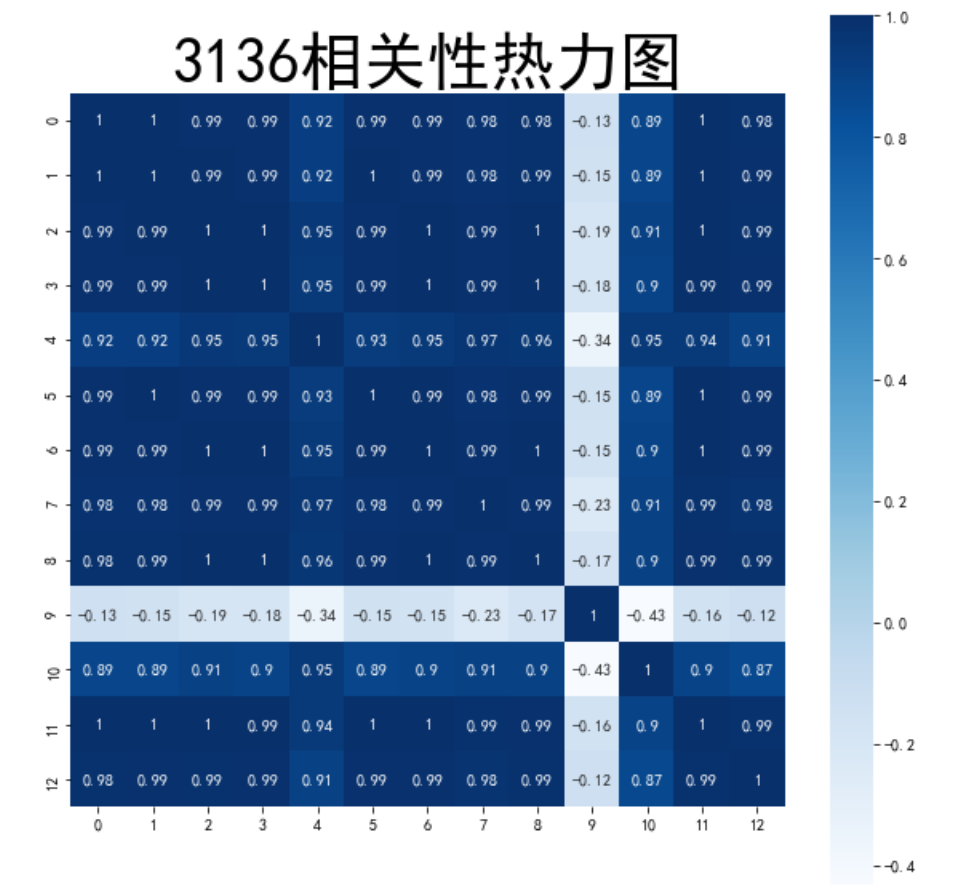
#相关性热力图
corr2=np.corrcoef(df.T)
import seaborn as sns
plt.subplots(figsize=(10,10))
sns.heatmap(corr2,annot=True,vmax=1,square=True,cmap="Blues")
plt.show()
plt.close()
#灰色预测
import sys
import pandas as pd
import numpy as np
from GM11 import GM11
inputfile1=r"C:\Users\ying\Desktop\new_reg_data.xlsx"
inputfile2=r"C:\Users\ying\Desktop\data.csv"
new_reg_data = pd.read_excel(inputfile1)
data = pd.read_csv(inputfile2)
new_reg_data.index = range(1994, 2014)
new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
cols = ['x1', 'x3', 'x4', 'x5','x6', 'x7', 'x8', 'x13']
for i in cols:
f = GM11(new_reg_data.loc[range(1994, 2014), i].values)[0]
new_reg_data.loc[2014,i] = f(len(new_reg_data)-1) # 2014年预测结果
new_reg_data.loc[2015,i] = f(len(new_reg_data)) # 2015年预测结果
new_reg_data[i] = new_reg_data[i].round(2) # 保留2位小数
outputfile = r"C:\Users\ying\Desktop\new_reg_data_GM11.xlsx"# 灰色预测后保存的路径
y = list(data['y'].values) # 提取财政收入列,合并至新数据框中
y.extend([np.nan, np.nan])
new_reg_data['y'] = y
new_reg_data.to_excel(outputfile) # 结果输出
print('预测结果为:\n', new_reg_data.loc[2014:2015,:]) # 预测展示

#支持向量回归预测模型
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
inputfile=r"C:\Users\ying\Desktop\new_reg_data_GM11.xlsx"
data=pd.read_excel(inputfile)
feature=['x1', 'x3', 'x4', 'x5','x6', 'x7', 'x8', 'x13']
data.index = range(1994, 2016)
data_train=data.loc[range(1994,2014)].copy()
data_mean=data_train.mean()
data_std=data_train.std()
data_train=(data_train-data_mean)/data_std
x_train=data_train[feature].values
y_train=data_train['y'].values
linearsvr=LinearSVR()
linearsvr.fit(x_train,y_train)
x=((data[feature]-data_mean[feature])/data_std[feature]).values#预测,并还原结果
data[u'y_pred']=linearsvr.predict(x)*data_std['y']+data_mean['y']
outputfile=r"C:\Users\ying\Desktop\new_reg_data_GM11_revenue.xlsx"
data.to_excel(outputfile)
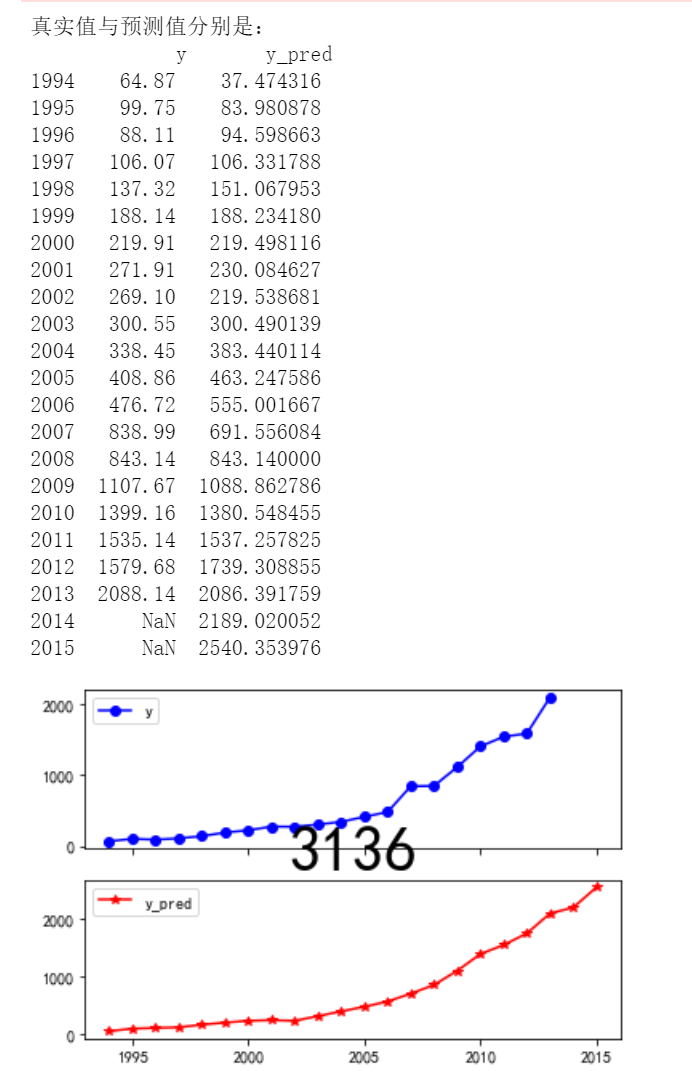
print('真实值与预测值分别是:\n',data[['y','y_pred']])
fig =data[['y','y_pred']].plot(subplots=True,style=['b-o','r-*'])
plt.show()
#ARIMA时间序列预测
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from pylab import mpl
# 画图中文
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
data_df = pd.read_excel(r"C:\Users\ying\Desktop\new_reg_data.xlsx")
#data_df.columns = ["时间", "电量"]
data_df.head()
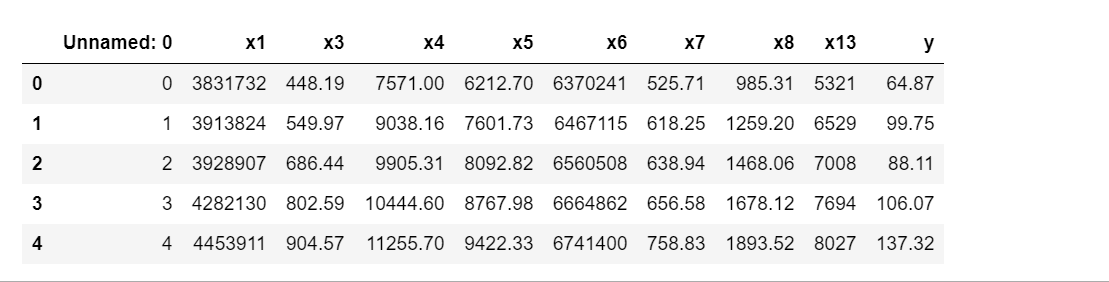
data_df[["y"]].plot()
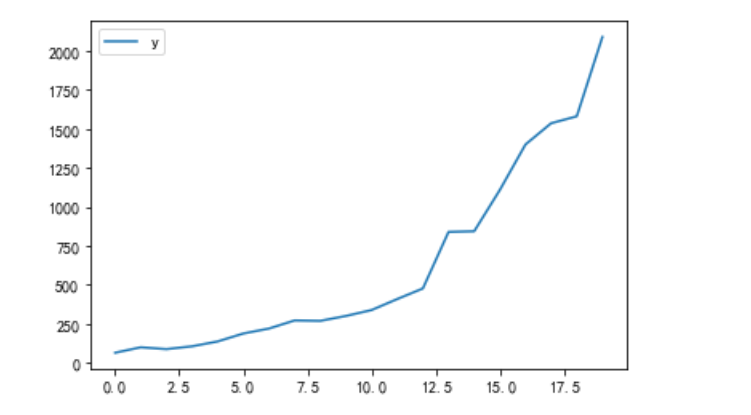
# 训练集、测试集
train_df = data_df.iloc[:20,:]
test_df = data_df.iloc[20:,:]
# 训练
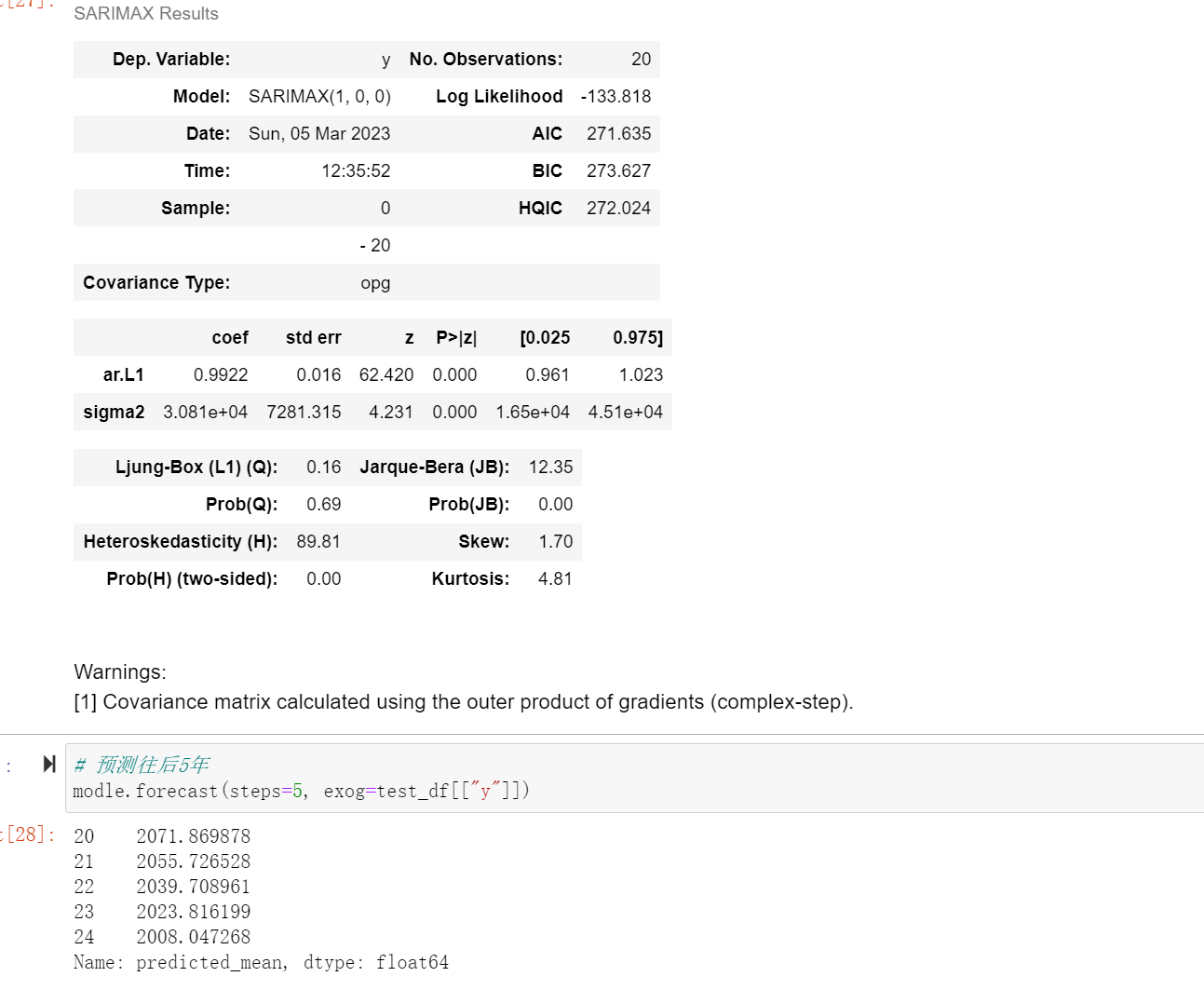
modle = sm.tsa.statespace.SARIMAX(train_df["y"]).fit(disp=-1)
modle.summary()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号