Flash与3D编程探秘(六)- 全方位旋转摄像机
日期:2008年11月
前面讨论过了如何横向旋转和移动摄像机,希望你已经完全理解,因为本文中的内容紧接着上一篇。回想一下,在前面制做的动画中,摄像机的旋转一直是围绕着y轴(竖直向上的轴)旋转,然而现实中我们可以上下旋转摄像机,甚至可以把摄像机倾斜一定角度,这就提醒了大家还需要更深入的研究旋转这个课题。下面几个动画演示了摄像机(简单的摄像机轮廓)3种旋转模式,从左到右分别是横向旋转,纵向旋转,倾斜。从3D空间角度来说,分别是沿y,x和z轴旋转。
(非常抱歉,下面的Flash文件不再支持)
横向和纵向旋转摄像机
倾斜摄像机
再介绍一些三角函数方程
事情变得复杂起来了!不过请你还是保持头脑清醒,这一篇文章你的任务就是学会纵向旋转和倾斜摄像机。你也许会想,我已经学会了横向旋转摄像机,算法中使用了一个panning的变量代表旋转角度,那么我再加两个变量,然后按顺序先沿x旋转,然后再沿y,最后z旋转不就好了。Well,这种想法很接近但却是错的(不要把3D数学想的那么简单)。来看一下下面的两个图,还是以3D空间在2D平面上的投影举例,把线段OB沿着z轴(也就是2D平面上 的原点)旋转大约78度,可以看到OB的长度就是我们的旋转半径。那么接下来,把OB沿y轴旋转,看一下图中的旋转半径是多少?不难看出,旋转半径明显的变小了。继续,如果你沿y旋转后,再打算沿x轴旋转,你还是会有同样“半径变化”的问题。

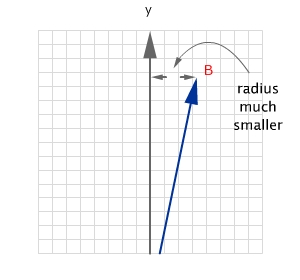
先沿z轴旋转再试图沿y旋转
在上面的例子中,如果想要保持旋转半径不变,那么一开始就不要有旋转角度。不过拿着摄像机左转右转,怎么可能保持角度不变!?因此你要在每一次摄像机旋转后,计算新的旋转半径。可是如果每一次都把旋转半径计算出来,那一定是很头疼!
于是人们聪明的想到了省力的方法。先来再看一下2D的三角函数(又是三角函数),根据旋转半径和旋转角度可以得到x和y:
y = Math.sin(angle)*radius;
需要注意一点,上面的方程式旋转点为原点,并且之前旋转角度为0。如果之前就有旋转角度a,再旋转b,那么方程式就成了:
y = Math.sin(a+b)*radius;
看起来眼熟,但是不知道是什么了?别担心:
sin(a+b) = sin(a)*cos(b) + sin(b)*cos(a);
把cos(a+b)和sin(a+b)带入上面的x和y求值方程我们就有:
y = radius*sin(a)*cos(b) + radius*sin(b)*cos(a);
化简一下得到:
y = x_before*sin(b) + y_before*cos(b);
这样,使用上面两个方程,不用担心你在其他平面(xz或者yz平面)的旋转角度,也不用每一次旋转后再去计算物体新的旋转半径了,只要关心旋转后的x和y,并且把它们作为下一次旋转的x_before和y_before,问题就解决了。下面我把相应的方程式写上:
围绕y轴旋转pan角度:
z = Math.sin(pan)*x_before + Math.cos(pan)*z_before;
围绕x轴旋转pitch角度:
z = Math.sin(pitch)*y_before + Math.cos(pitch)*z_before;
围绕z轴旋转tilt角度:
y = Math.sin(tilt)*x_before + Math.cos(tilt)*y_before;
那么基本的知识已经说完了。总结一下,当你在使用这些方程式操作摄像机全方位旋转的时候,只要取得相应的变量,然后替换在方程里就可以了。是不是看起来有点难理解?不要担心,适应这些东西是需要花一点时间(特别是这些对你来说还是新课题的话),不过适应以后你应该就觉得很简单了。坦白的说,其实你并不需要知道到底这些是怎样得来的,你只要知道如何使用它们,得到想要得结果就可以了(当然完全理解会对你以后的学习有一些帮助)。这些方程你可以写成一个函数,然后命名它为“给我旋转”方程,当你需要摄像机旋转的时候,只要呼唤“给我旋转”就好了,至于“给我旋转”怎么做的工作,你就不需要担心了。
全方位旋转摄像机
只说这些理论的东西,你肯定会觉得乏味,那么我举个例子来说明。下面这个程序演示了摄像机的全方位旋转,运行程序你会看到你置身在一个巨大的正方体中,这个正方体是由很多我们的朋友小P组成的,不过这回用不同颜色的小P来代表不同的边。使用WS键控制纵向旋转,AD键控制横向旋转,QE控制倾斜角度,鼠标点击屏幕禁止或者允许鼠标移动控制纵向和横向旋转。
(非常抱歉,下面的Flash文件不再支持)
全方位旋转摄像机,使用WS纵向旋转,AD横向旋转,QE倾斜角度,鼠标点击禁止或者允许鼠标控制
制作步骤:
1. 首先定义几个常量,MAX_OBJ是每条边上的物体数量,CUBE_WIDTH是正方体的边长。
var MAX_OBJ =6;
var PI = 3.1415926535897932384626433832795;
var CUBE_WIDTH = 300;
2. 下面还是设置原点,场景,焦距等。
var origin = new Object();
origin.x = stage.stageWidth/2;
origin.y = stage.stageHeight/2;
origin.z = 0;
var scene = new Sprite();
scene.x = origin.x;
scene.y = origin.y;
this.addChild(scene);
var focal_length =400;
3. 设置摄像机,这回的摄像机多了几个新的属性,pitching是纵向旋转角度,tilt是倾斜的角度。
camera.x = 0;
camera.y = 0;
camera.z = 0;
camera.panning = -PI/8; // init pan angle of our camera, pan left
camera.pitching = -PI/8; // pitch up
camera.tilt = 0; // and no tilt
4. 设置一些全局变量,在处理键盘和鼠标事件时会用到。
var pan_left;
var pan_right;
var pitch_up;
var pitch_down;
var mouse_ctl = true;
5. 下面布置一个正方体,你完全不必要明白我是怎么布置场景的,因为布置场景的方式并不唯一,所以如果你愿意的话,你可以自己动手布置3D场景,当然我也不介意直接拷贝我的设置场景的代码去用。总之,这些代码就是初始化一些小P,然后把它们摆放在合适位置(围绕着摄像机)。
// cause every body has a different way of doing that, if you really
// interested in how i did it, then you may have a look
// you can just copy my code and it will set it up for you
var len = CUBE_WIDTH/2;
for (var seg = 0; seg < 3; seg++)
{
var line_h;
var line_v;
var line_z;
switch (seg)
{
case 0:
line_h = true;
line_v = false;
line_z = false;
break;
case 1:
line_h = false;
line_v = true;
line_z = false;
break;
case 2:
line_h = false;
line_v = false;
line_z = true;
break;
}
for (var i = 0; i < MAX_OBJ; i++)
{
if (line_h || (i == 0 || i == MAX_OBJ-1))
{
for (var j = 0; j < MAX_OBJ; j++)
{
if (line_v || (j == 0 || j == MAX_OBJ-1))
{
for (var k = 0; k < MAX_OBJ; k++)
{
if (line_z || (k == 0 || k == MAX_OBJ-1))
{
var ball;
if (line_h)
{
ball = new SphereHorizontal();
if ((i == 0 || i == MAX_OBJ-1))
{
ball = new SphereVertex();
}
else
{
ball = new SphereHorizontal();
}
}
if (line_v)
{
ball = new SphereVertical();
if ((j == 0 || j == MAX_OBJ-1))
{
continue;
}
}
if (line_z)
{
ball = new SphereStraight();
if ((k == 0 || k == MAX_OBJ-1))
{
continue;
}
}
ball.x_3d = -len + (i)*(CUBE_WIDTH/MAX_OBJ);
ball.y_3d = -len + (j)*(CUBE_WIDTH/MAX_OBJ);
ball.z_3d = -len + (k)*(CUBE_WIDTH/MAX_OBJ);
scene.addChild(ball);
}
}
}
}
}
}
}
6. 下面的函数就是刷新小P位置和大小的函数,这也是这篇文章主要讲述的内容,所以,请集中。OK,首先要得出小P(其中一个小P)到摄像机的x,y和z 距离。对于横向旋转角度panning,使用本文前面讲述的方程,把相应的x距离和z距离带入,然后得出新的x距离和z距离。使用相同的方法得出 纵向旋转角度pitching后的y和z距离,对摄像机倾斜角度tilt再次使用上述方程。这样就得到围绕三个轴旋转后新的x,y和z距离,继而便可以使用老办法算出物体的缩放和移动。最后别忘记加一个z_near变量,存储小P到摄像机的距离,以便于对所有小P进行z排序。
// here is what we really care about, so concentrate
function display(obj)
{
var x_distance = obj.x_3d - camera.x; // first we determine x distance ball to camera
var y_distance = obj.y_3d - camera.y; // y
var z_distance = obj.z_3d - camera.z; // z distance
var tempx, tempy, tempz; // some temporary variables
// two more trig you need to know about, suppose a is the previous angle
// cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
// sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b)
// thus we have the following
var angle = camera.panning;
tempx = Math.cos(angle)*x_distance - Math.sin(angle)*z_distance;
tempz = Math.sin(angle)*x_distance + Math.cos(angle)*z_distance;
x_distance = tempx;
z_distance = tempz;
angle = camera.pitching; // the same thing we have for pitch angle
tempy = Math.cos(angle)*y_distance - Math.sin(angle)*z_distance;
tempz = Math.sin(angle)*y_distance + Math.cos(angle)*z_distance;
y_distance = tempy;
z_distance = tempz;
angle = camera.tilt; // and tilt angle
tempx = Math.cos(angle)*x_distance - Math.sin(angle)*y_distance;
tempy = Math.sin(angle)*x_distance + Math.cos(angle)*y_distance;
x_distance = tempx;
y_distance = tempy;
if (z_distance > 0) // if the ball isin front of the camera
{
if (!obj.visible)
obj.visible = true; // make the ball visible anyway
var scale = focal_length/(focal_length+z_distance); // cal the scale of the ball
obj.x = x_distance*scale; // calcualte the x position in a camera view
obj.y = y_distance*scale; // and y position
obj.scaleX = obj.scaleY = scale; // scale the ball to a proper state
}
else
{
obj.visible = false;
}
obj.z_near = z_distance; // keep track of z distance to our camera
}
7. 写一个循环函数,不停的调用第6步的函数刷新所有的小P。如果你一直有看文章的话那么这些对你来说应该不难。
function run(e:Event)
{
for (var i = 0; i < scene.numChildren; i++) // update all the balls on the screen
{
display(scene.getChildAt(i));
}
swap_depth(scene);
}
// bubble sort algo
function swap_depth(container:Sprite)
{
for (var i = 0; i < container.numChildren - 1; i++)
{
for (var j = container.numChildren - 1; j > 0; j--)
{
if (Object(container.getChildAt(j-1)).z_near < Object(container.getChildAt(j)).z_near)
{
container.swapChildren(container.getChildAt(j-1), container.getChildAt(j));
}
}
}
}
8. 最后是设置一些键盘和鼠标事件响应函数,完成我们的程序。
{
if (e.keyCode == 65) // a
pan_left = true;
if (e.keyCode == 68) // d
pan_right = true;
if (e.keyCode == 87) // w
pitch_up = true;
if (e.keyCode == 83) // s
pitch_down = true;
}
function key_up(e:KeyboardEvent):void
{
if (e.keyCode == 65)
pan_left = false;
if (e.keyCode == 68)
pan_right = false;
if (e.keyCode == 87)
pitch_up = false;
if (e.keyCode == 83)
pitch_down = false;
}
function key_response(e:Event):void
{
if (pan_left)
camera.panning -= 0.01;
if (pan_right)
camera.panning += 0.01;
if (pitch_up)
camera.pitching -= 0.01;
if (pitch_down)
camera.pitching += 0.01;
if (mouse_ctl) // if allow mouse control pan and pitch
{
camera.panning += scene.mouseX/22000;
camera.pitching += scene.mouseY/22000;
}
// limit the pitch and tilt
if (camera.pitching < -1*PI/3)
camera.pitching = -1*PI/3;
if (camera.pitching > PI/3)
camera.pitching = PI/3;
}
function clicked(e:Event) // toggle mouse control
{
mouse_ctl = !mouse_ctl;
}
// setup event listeners
this.addEventListener(Event.ENTER_FRAME, run);
this.addEventListener(Event.ENTER_FRAME, key_response);
stage.addEventListener(KeyboardEvent.KEY_DOWN, key_down);
stage.addEventListener(KeyboardEvent.KEY_UP, key_up);
stage.addEventListener(MouseEvent.CLICK, clicked);
总结一下,这篇文章中的三角函数部分可能有些抽象,因为是在3D空间中完成的,如果你把所有的例子首先映射到2D平面上会想对好理解一些。不过还是那句话,不要担心,你只要知道如何使用这些方程就可以了。
注意:物体自身围绕中心的3D旋转
有一点不知道你有没有注意,那就是在本文的开头,我做了几个摄像机的旋转演示。在演示里,摄像机(物体)都是本身在旋转,而并不是我们的眼睛(摄像机)在旋转。虽然到目前为止的文章里,还没有讨论到如何让物体自身旋转,不过很快就会看到一些例子。注:我做这些演示唯一想说明的就是三种旋转的机制,所以请不要着急那些演示是怎么做出来的。
其实,关于Flash和3D空间的基本知识的介绍到这里我想应该结束了,从下篇文章开始就要关注3D物体,因此,如果对前面文章中的基础知识还是模模糊糊的话,完全可以不必担心。不过我还是建议你自己多实验一些小例子,增加自己的空间感。相信你在不久的将来就可以开发自己的3D Engine了,加油,ALL THINGS ARE POSSIBLE!
非常抱歉,文中暂时不提供源文件下载,如果你需要源文件,请来信或者留言给我。
|
|
作者:Yang Zhou 出处:http://yangzhou1030.cnblogs.com 本文版权归作者和博客园共有,转载未经作者同意必须保留此段声明。请在文章页面明显位置给出原文连接,作者保留追究法律责任的权利。 |
posted on 2008-11-06 15:27 yangzhou1030 阅读(5656) 评论(11) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号