自适应滤波:维纳滤波器——LCMV及MVDR实现
作者:桂。
时间:2017-03-24 06:52:36
链接:http://www.cnblogs.com/xingshansi/p/6609317.html
声明:欢迎被转载,不过记得注明出处哦~

【读书笔记03】
前言
西蒙.赫金的《自适应滤波器原理》第四版,上一篇看到维纳滤波基本形式:最优化问题,且无任何条件约束。这次看到有约束的部分,简单整理一下思路:
1)拉格朗日乘子法;
2)线性约束最小方差滤波器(Linearly constrained minimum-variance,LCMV);
3)谱估计之MVDR算法(Minimum variance distortionless response ,MVDR);
内容为自己的学习总结,如有错误之处,还请各位帮忙指出!
一、拉格朗日乘子法
学习到含有约束条件的Wiener Filter,拉格朗日乘子法是解决:将含约束条件的优化问题转化为无约束条件优化问题的途径,故先梳理一下。
A-只含一个等式约束的最优化
实函数$f\left( {\bf{w}} \right)$是参数向量${\bf{w}}$的二次函数,约束条件是:
${{{\bf{w}}^H}{\bf{s}} = g}$
其中$\bf{s}$是已知向量,$g$是复常数。例如在波束形成应用中${\bf{w}}$表示各传感器输出的一组复数权值,$\bf{s}$是一个旋转向量。假设该问题是一个最小化问题,令$c\left( {\bf{w}} \right) = {{\bf{w}}^H}{\bf{s}} - g = 0 + j0$可以描述为:
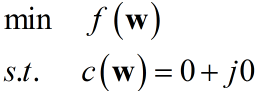
所谓拉格朗日乘子法,就是引入拉格朗日乘子:将上述约束最小化问题转化为无约束问题,定义一个新的实函数:
$h\left( {\bf{w}} \right) = f\left( {\bf{w}} \right) + {\lambda _1}{\mathop{\rm Re}\nolimits} \left[ {c\left( {\bf{w}} \right)} \right] + {\lambda _2}{\mathop{\rm Im}\nolimits} \left[ {c\left( {\bf{w}} \right)} \right]$
现在定义一个复拉格朗日乘子:
$\lambda = {\lambda _1} + {\lambda _2}$
$h({\bf{w}})$改写为:
$h\left( {\bf{w}} \right) = f\left( {\bf{w}} \right) + {\mathop{\rm Re}\nolimits} \left[ {{\lambda ^*}c\left( {\bf{w}} \right)} \right]$
至此,无约束优化问题转化完成,利用偏导求参即可,其实这是一个简化的形式,分别求解$\lambda _1$、$\lambda _2$也是一样的。
B-包含多个等式约束的最优化
实函数$f\left( {\bf{w}} \right)$是参数向量${\bf{w}}$的二次函数,约束条件是:
${{{\bf{w}}^H}{\bf{s_k}} = g_k}$
其中$k = 1,2...K$,方法同单个约束情况相同,求解伴随方程:
$\frac{{\partial f}}{{\partial {{\bf{w}}^*}}} + \sum\limits_{k = 1}^K {\frac{\partial }{{\partial {{\bf{w}}^*}}}\left( {{\mathop{\rm Re}\nolimits} \left[ {\lambda _k^*{c_k}\left( {\bf{w}} \right)} \right]} \right)} = {\bf{0}}$
此时与多个等式约束联合成方程组,这个方程组定义了${\bf{w}}$和拉格朗日乘子${\lambda _1}$、${\lambda _2}$...${\lambda _K}$的解。
二、线性约束最小方差滤波器
之前看到的维纳滤波都是基于最小均方误差准则,而没有添加任何约束,此处考虑含有线性约束情况下的方差滤波器,文中给了一个图:
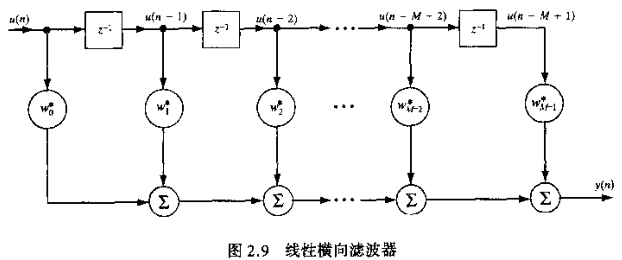
其中$x(n)$为输入信号(即$u$,为了与下文统一,用$x$表示),$w_i$为权重,$y(n)$为滤波器输出:
$y\left( n \right) = \sum\limits_{k = 0}^{M - 1} {{w^*_k}x\left( {n - k} \right)} $
这个优化问题如果没有约束可以表述为:
$\arg \mathop {\min }\limits_{\bf{w}} J = E\left[ {{y^H}y} \right]$
假设$\theta_0$为目标达到角,希望对该角度特殊处理:如果该角是目标角,希望其幅度保持不衰减,即$\sum\limits_{k = 0}^{M - 1} {{w^*_k}{e^{ - jk{\theta _0}}}} = 1$;反之,如果是干扰信号,希望其幅度衰减为0,即$\sum\limits_{k = 0}^{M - 1} {{w^*_k}{e^{ - jk{\theta _0}}}} = 0$;无论是0还是1,都是对优化问题的一种约束形式,写出更一般的约束形式:
$\sum\limits_{k = 0}^{M - 1} {{w^*_k}{e^{ - jk{\theta _0}}}} = g$
$g$是一个复增益。利用拉格朗日乘子法给出约束条件下准则函数(暂不考虑噪声情况):
$J = {{\bf{w}}^H}{R_{xx}}{\bf{w}} + {\mathop{\rm Re}\nolimits} \left[ {{\lambda ^*}\left[ {{{\bf{w}}^H}{\bf{s}}\left( {{\theta _0}} \right) - g} \right]} \right]$
其中${\bf{s}}\left( {{\theta _0}} \right) = \left[ {1,{e^{ - j{\theta _0}}},...,{e^{ - j(M - 1){\theta _0}}}} \right]$,$M$是权向量$\bf{w}$的个数,则到系数解:
$\lambda = - \frac{{2g}}{{{{\bf{s}}^H}\left( {{\theta _0}} \right){{\bf{R}}^{ - 1}}{\bf{s}}\left( {{\theta _0}} \right)}}$
对应最优权向量:
${{\bf{w}}_{opt}} = \frac{{{g^*}{{\bf{R}}^{ - 1}}{\bf{s}}\left( {{\theta _0}} \right)}}{{{{\bf{s}}^H}\left( {{\theta _0}} \right){{\bf{R}}^{ - 1}}{\bf{s}}\left( {{\theta _0}} \right)}}$
以权向量${{\bf{w}}_{opt}}$表征的波束形成器称为线性约束最小方差(LCMV, linearly constrained minimum-variance)波束形成器,也称LCMV滤波器。
三、LCMV应用——MVDR算法
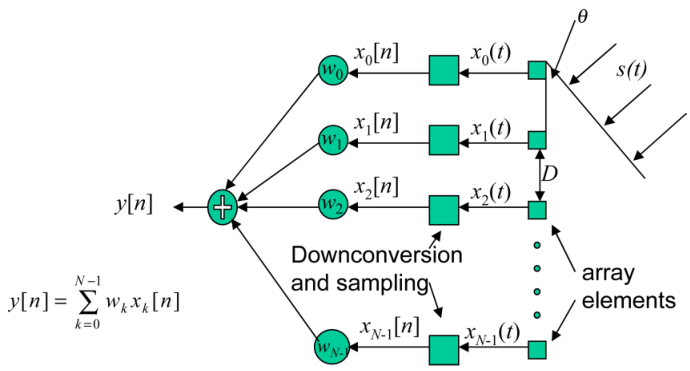
实际应用中信号掺杂了噪声。假设原信号$s(t)$,接收器收集的是不同时延的混合信号,经过采样量化后得$x(n)$,现在希望通过自适应权重$w$输出符合需求的$y$,假设通道个数为$N$,给出接收通道模型:
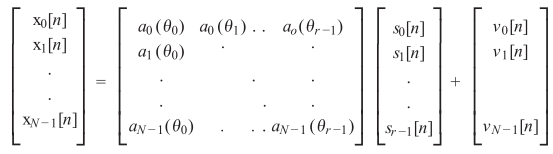
写成矩阵形式:
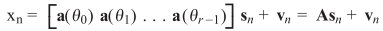
进行相关矩阵求解:

可以发现如果$w^Hw$为定值,则噪声对最优权值的求解无影响,LCMV可用。
给出混合模型:
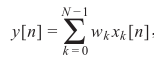
对应准则函数(此处$g = 1$):
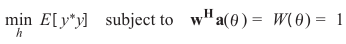
借助LCMV的分析,得出MVDR最优权重:
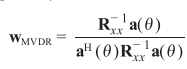
实际应用中,通常用时间换空间,借助遍历性近似求解相关矩阵:
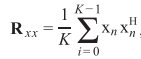
给出代码:
doas=[-30 -5 40]*pi/180; %DOA's of signals in rad.
P=[1 1 1]; %Power of incoming signals
N=10; %Number of array elements
K=1024; %Number of data snapshots
d=0.5; %Distance between elements in wavelengths
noise_var=40; %Variance of noise
r=length(doas); %Total number of signals
% Steering vector matrix. Columns will contain the steering vectors of the r signals
A=exp(-i*2*pi*d*(0:N-1)'*sin([doas(:).']));
% Signal and noise generation
sig=round(rand(r,K))*2-1; % Generate random BPSK symbols for each of the
% r signals
noise=sqrt(noise_var/2)*(randn(N,K)+i*randn(N,K)); %Uncorrelated noise
X=A*diag(sqrt(P))*sig+noise; %Generate data matrix
R=X*X'/K; %Spatial covariance matrix
%MVDR
IR=inv(R); %Inverse of covariance matrix
for k=1:length(angles)
mvdr(k)=1/(a1(:,k)'*IR*a1(:,k));
end
figure;
plot(angles,abs(mvdr)/max(abs(mvdr)),'k');hold on;
xlabel('Angle in degrees')
%Estimate DOA's using the classical beamformer
for k=1:length(angles)
Classical(k)=(a1(:,k)'*R*a1(:,k));
end
plot(angles,abs(Classical)/max(abs(Classical)),'r--');grid on;
legend('MVDR','Classical Beamformer');
对应结果图:
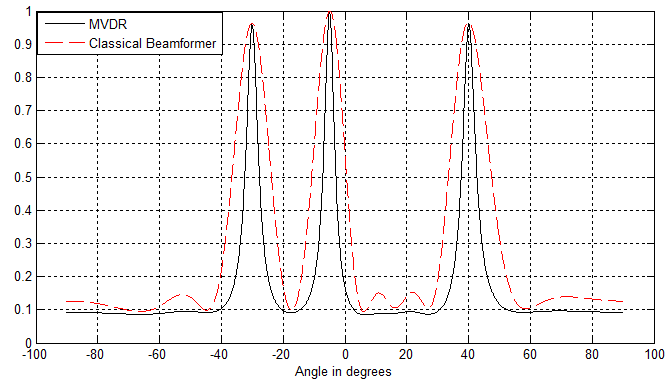
噪声较大时:

二者就比较接近,可以发现:
- 信号与噪声不相关、且噪声为白噪声时,仍能求解最优权值;
- 噪声较大时,MVDR与无约束最优滤波效果接近,此时MVDR的优势不再明显,这也容易理解,噪声占主要成分时对波束的约束保留效果不再明显。
两点补充:
1)因为LCMV中有矩阵求逆一项,所以补充说明一点:默认不同角度信号不相干,只记录学习的理论知识,不论及技术细节处。
2)基于窄带分析。如果是宽带,则可以划分多个自带,或者利用聚焦矩阵预处理,窄带才有如下近似(且一个频带内才可以用一个频率表征):
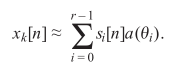
参考:
Jeffrey Foutz, Andreas Spanias, and Mahesh K. Banavar《Narrowband Direction of Arrival Estimation for Antenna Arrays》.
Simon Haykin 《Adaptive Filter Theory Fourth Edition》.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号