曲线拟合——(2)拉普拉斯/瑞利/对数正态 曲线
作者:桂。
时间:2017-03-15 21:12:18
链接:http://www.cnblogs.com/xingshansi/p/6556517.html
声明:欢迎被转载,不过记得注明出处哦~

| 本文为拟合系列中的一部分,主要介绍拉普拉斯曲线 、瑞利曲线、对数正态曲线的拟合,并给出理论推导。 |
一、理论分析
A-拉普拉斯(Laplace)
对于拉普拉斯分布:
$f(x) = \frac{1}{{2b}}{e^{ - \frac{{\left| {x - \mu } \right|}}{b}}}$
假设数据点{$x_i$,$y_i$}($i = 1,2,3,...N$)符合Laplace分布曲线,对其进行拟合(曲线拟合不同于分布拟合,需要乘以幅度$A$),给出准则函数:
 对准则函数$J_0$求解即可实现参数估计。
对准则函数$J_0$求解即可实现参数估计。
由于求导比较复杂(可以借助Mathmatica/Maple),因此这里换一个思路:如果$e^x$—>$y$,则$x$—>$lny$,重新定义准则函数:
 后续求参就方便了。
后续求参就方便了。
给出调用fit实现的代码:
clc;clear all;close all;
%generate the orignal data
mu = 3;
b = 2;
A = 4;
x=-10:.1:10;
y=A/2/b*exp(-abs(x-mu)/b)+0.05*randn(1,length(x));
subplot 211
scatter(x,y,'k');grid on;
%%curve fitting
%2-Laplace distribution
f = fittype('a*exp(-(abs(x-b)/c))');
[cfun,gof] = fit(x(:),y(:),f);
yo = cfun.a*exp(-(abs(x-cfun.b)/cfun.c));
%plot
subplot 212
scatter(x,y,'k');hold on;
grid on;
plot(x,yo,'g--','linewidth',2);
对应结果图: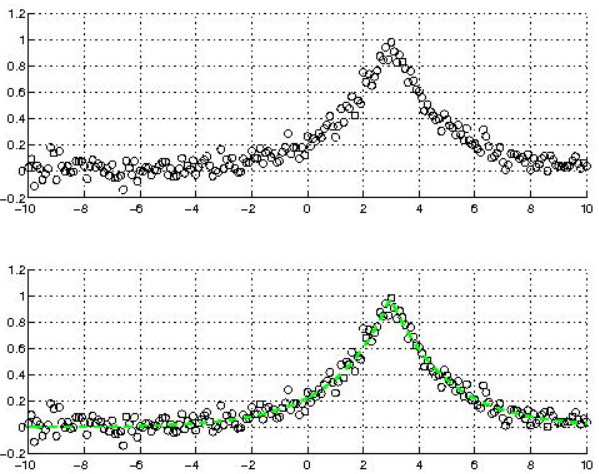
B-瑞利(Rayleigh)
对于瑞利分布:
$f(x) = \frac{x}{{{\sigma ^2}}}{e^{ - \frac{{{x^2}}}{{2{\sigma ^2}}}}}$
给出准则函数:
 只涉及一个参数$\sigma$,同样是利用对数转化,进而求取参数估计。
只涉及一个参数$\sigma$,同样是利用对数转化,进而求取参数估计。
C-对数正态(Log-normal)
对数正态就是正态分布的变形,即$lnx$—>$x$,求参过程完全一致,可以参考:正态曲线拟合。
二、拟合优化
对于求取对数的估计准则,都会有误差在0处较大的问题。关于优化的小trick,在分析正态分布曲线拟合时,已经给出详细理论,此处不再展开。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号